Chemisches Gleichgewicht

Die meisten chemischen Reaktionen sind umkehrbar. Das bedeutet, dass eine Reaktion in beide Richtungen stattfindet. Bei solchen umkehrbaren Reaktionen stellt sich irgendwann ein sogenanntes chemisches Gleichgewicht ein.

Dazu ein nicht-chemisches Beispiel:

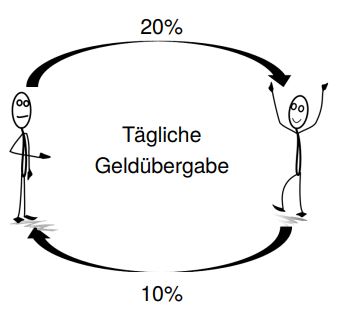
Wir stellen uns vor, wir haben 50 Euro und unser Freund hat 10 Euro. Wir möchten ihn unterstützen, indem wir ihm täglich 20% von unserem Geld geben, erwarten im Gegenzug aber täglich 10% von seinem Geld. Jeden Tag gibt es eine entsprechende Geldübergabe.

In der folgenden Tabelle sind die Geldbeträge, die wir und unser Freund an den jeweiligen Tagen nach der Geldübergabe haben, aufgeführt.

\begin{array}{|c|c|c|}\hline
{\textbf{Tag}} &
{\textbf{Wir}} &
{\textbf{Unser Freund}} \\
\hline
1 &
\text{41,00 €} &
\text{19,00 €} \\
\hline
2 &
\text{34,70 €} &
\text{25,30 €} \\
\hline
3 &
\text{30,29 €} &
\text{29,71 €} \\
\hline
\cdot \cdot \cdot &
\cdot \cdot \cdot &
\cdot \cdot \cdot \\
\hline
25 &
\text{20,00 €} &
\text{40,00 €} \\
\hline
26 &
\text{20,00 €} &
\text{40,00 €} \\
\hline
\end{array}

Ab dem 25. Tag ändert sich an dem Geldbetrag den wir jeweils haben nichts mehr, auch wenn weiterhin die Geldanteile übergeben werden. Wir geben unserem Freund jetzt jeden Tag 4 Euro und er gibt uns auch 4 Euro. Es hat sich jetzt trotz der weiteren täglichen Übergabe ein Gleichgewicht eingestellt Nehmen wir dieselbe Situation, aber jetzt starten wir mit 0 Euro und unser Freund
mit 60 Euro. Die Geldbeträge ändern sich dann wie folgt:

\begin{array}{|c|c|c|}\hline
{\textbf{Tag}} &
{\textbf{Wir}} &
{\textbf{Unser Freund}} \\
\hline
1 &
\text{6,00 €} &
\text{54,00 €} \\
\hline
2 &
\text{10,20 €} &
\text{49,80 €} \\
\hline
3 &
\text{13,14 €} &
\text{46,86 €} \\
\hline
\cdot \cdot \cdot &
\cdot \cdot \cdot &
\cdot \cdot \cdot \\
\hline
25 &
\text{20,00 €} &
\text{40,00 €} \\
\hline
26 &
\text{20,00 €} &
\text{40,00 €} \\
\hline
\end{array}

Nach einer gewissen Zeit haben wir wieder die selben Gelbeträge. Bei umkehrbaren chemischen Reaktionen verhält es sich genauso: es gibt eine Hin- und eine Rückreaktion, welche in bestimmten Geschwindigkeiten ablaufen. Unabhängig davon, mit welchen Mengen wir beginnen, liegt am Ende dasselbe Stoffmengenverhältnis vor.

Betrachten wir hierfür eine chemische Reaktion als Beispiel:

\begin{align*}
H_2+I_2 \leftrightarrow 2 HI
\end{align*}

Bei dieser Reaktion handelt es sich um eine umkehrbare Reaktion.

\begin{align*}
\text{Hinrekation:} \quad H_2+I_2 \rightarrow 2 HI \\
\text{Rückreaktion:} \quad 2 HI \rightarrow H_2+I_2
\end{align*}

Beide Reaktionen laufen mit einer bestimmten Reaktionsgeschwindigkeit ab, welche unter anderem von der Konzentration der jeweiligen Edukte abhängt.

\begin{array}{ll}
Geschwindigkeit Hinreaktion: & v_{\text{hin}} = k_{\text{hin}} \cdot c(H_2) \cdot c(I_2) \\
Geschwindigkeit Rückreaktion: & v_{\text{rück}} = k_{\text{rück}} \cdot c(HI) \cdot c(HI) = k_{\text{rück}} \cdot c(HI)^2
\end{array}

khin und krück sind die jeweiligen Reaktionskonstanten der Hin- und Rückreaktion. Bei der Geschwindigkeit der Rückreaktion müssen wir beachten, dass zwei Wasserstoffiodid-Moleküle vorliegen und die Konzentration des Wasserstoffiodids daher zweimal in die Berechnung der Reaktionsgeschwindigkeit eingeht. Sobald sich eine Reaktion im Gleichgewicht befindet, sind die beiden Reaktionsgeschwindigkeiten gleich groß. Es ergibt sich daher folgender Zusammenhang:

\begin{array}{crcll}
& v_{\text{hin}} & = & v_{\text{rück}} & \\
\Rightarrow & k_{\text{hin}} \cdot C_{\text{GG}}({H_2}) \cdot C_{\text{GG}}({I_2}) & = & k_{\text{rück}} \cdot c_{\text{GG}}({HI})^2 & |:k_{\text{rück}} \\
\Leftrightarrow & \frac{k_{\text{hin}}}{k_{\text{rück}}} \cdot C_{\text{GG}}({H_2}) \cdot C_{\text{GG}}({I_2}) & = & C_{\text{GG}}({HI})^2 & |:\left(C_{\text{GG}}({H_2}) \cdot C_{\text{GG}}({I_2})\right) \\
\Leftrightarrow & \underbrace{\frac{k_{\text{hin}}}{k_{\text{rück}}}}_{=K_c} & = & \frac{C_{\text{GG}}({HI})^2}{C_{\text{GG}}({H_2}) \cdot C_{\text{GG}}({I_2})} & = \frac{C_{\text{GG}}(\text{Produkte})}{C_{\text{GG}}(\text{Edukte})}
\end{array}

Wir definieren den Bruch khin/krück als Gleichgewichtskonstante Kc. Die Gleichgewichtskonstante gibt eine Aussage über die Lage des Gleichgewichts. Mit den
Konzentrationen cGG in der Gleichung sind diejenigen gemeint, die vorliegen, wenn das Gleichgewicht sich eingestellt hat.

Übertragen auf das Geldbeispiel am Anfang bedeutet das Folgendes:
Die 20%, die wir unserem Freund geben, entsprechen der Reaktionskonstante der Hinreaktion khin. Die 10%, welche unser Freund uns gibt, entsprechen der Reaktionskonstante der Rückreaktion krück.

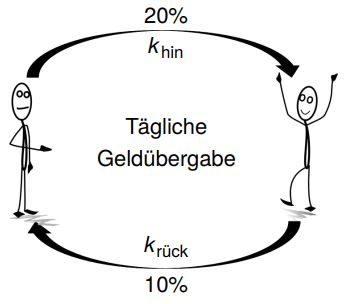
Die Konzentrationen der Edukte sind die jeweiligen Geldbeträge an den einzelnen Tagen, die wir besitzen und die Konzentrationen der Produkte entsprechend die Geldbeträge an den einzelnen Tagen, die unser Freund besitzt. Die Konzentration cGG(Edukte) im Gleichgewichtszustand sind die 20 Euro die wir am Ende unverändert besitzen und entsprechend cGG(Produkte) im Gleichgewicht die 40 Euro, die unser Freund am Ende unverändert besitzt. Zusammengefasst gilt hier also:

\begin{align*}
K_c =\frac{20\%}{10\%} = \frac{40 \ \text{Euro}}{20 \ \text{Euro}} = \frac{C_{\text{GG}}(\text{Produkte})}{C_{\text{GG}}(\text{Edukte})}
\end{align*}