
Hypothesentest vollständig erklärt
Auf diesem Artikel erklären wir dir das vollständige Vorgehen beim Hypothesentest. Wir gehen dabei auf folgende Themen & Schritte ein:
- Hypothesentest Einleitung
- Aufstellen der Hypothese
- Testgröße und Stichprobenlänge
- Entscheidungsregel: Annahme- und Ablehnungsbereich
- Wahrscheinlichkeiten bestimmen
- Fehler beim Testen
- Alternativtest
- Hypothesentest mit δ-Regeln
- Beidseitiger Hypothesentest
- Einseitiger Hypothesentest
- Hypothesentest mit Ablesen aus Tabelle
1,99€
Hypothesentest Einleitung
Hypothesentests werden immer dann durchgeführt, wenn man irgendetwas mit Hilfe von erhobenen Daten nachweisen möchte, zum Beispiel dass auf dem Oktoberfest die Maßkrüge nicht ganz vollgemacht werden. Der Grundsatz bei allen statistischen Tests ist hierbei, dass wir das Gegenteil widerlegen müssen – wir müssen also widerlegen, dass der Maßkrug tatsächlich mit einem Liter gefüllt ist.
Wir können uns diesen Grundsatz mit einer Gerichtsverhandlung vorstellen, denn wie es so schön heißt: Im Zweifel für den Angeklagten. Man geht davon aus, dass der Angeklagte unschuldig ist (ohne es genau zu wissen). Um von der Schuld des Angeklagten überzeugt zu werden, müssen ausreichend Beweise gesammelt werden, welche die Schuld ohne Zweifel darlegt. Falls nicht genug Beweise vorliegen, muss davon ausgegangen werden, dass er unschuldig ist. Wir können diesen Sachverhalt in statistischen Hypothesen zusammenfassen:
- $H_0$: Der Angeklagte ist unschuldig.
- $H_1$: Der Angeklagte ist schuldig.
Es stehen sich damit zwei einander widersprechende Behauptungen/Vermutungen (sog. Hypothesen) gegenüber.
Die Nullhypothese $H_0$, die geprüft werden soll und ihre logische Verneinung, die Alternativ- bzw. Gegenhypothese $H_1$. Die Begriffe sind hierbei so zu verstehen, dass geprüft wird, ob $H_1$ bewiesen werden kann, man also bei ergebnisloser Suche weiter $H_0$ als gültig erachtet.
Der Hypothesentest dient nun dazu anhand des Ergebnisses einer Stichprobe zu einer Entscheidung darüber zu kommen, welche der beiden Hypothesen man eher zu glauben bereit ist oder anders ausgedrückt: welche der beiden Hypothesen angenommen (bzw. beibehalten) und welche verworfen wird.
Eine 100%-ige Sicherheit, dass die angenommene Hypothese auch tatsächlich wahr ist, kann der Hypothesentest naturgemäß niemals bieten, da wir von einer Stichprobe auf die Grundgesamtheit schließen.
Zur Berechnung der Wahrscheinlichkeiten eines solchen Tests benutzt man die Binomialverteilung.
In diesem Abschnitt wollen wir euch eine grobe Übersicht zum Thema Testen geben. Dabei sei die Aussage: 30% lieben Mathe, welche unsere $H_0$ Hypothese sein soll. Mit Hilfe des Stichprobenumfangs $n=100$ (100 Schüler wurden befragt) und der Wahrscheinlichkeit $p=0,3$ kann die Wahrscheinlichkeitsverteilung dargestellt werden. Der höchste Wert der Verteilung entspricht dabei immer dem Erwartungswert.
Die folgende Abbildung zeigt uns, welcher Test infolge der Aufgabenstellung durchgeführt werden soll und wie die Gegenhypothese $H_1$ lauten muss.

Behauptet jemand etwas anderes, zum Beispiel das 40% Mathe lieben anstatt 30%, wird ein Alternativtest durchgeführt. Neben dem Alternativtest gibt es noch den einseitigen Hypothesentest, der links- oder rechtsseitig sein kann und den beidseitigen Hypothesentest.
In den nächsten Abschnitten werden wir sehen, wie solche Hypothesen aufgestellt werden, was es mit diesen Fehlern auf sich hat und wie wir Hypothestentests mit $\sigma$-Regeln und der Tabelle der Normalverteilung durchführen.
1,99€
Aufstellen der Hypothesen
Bevor man einen Hypothesentest durchführt, müssen die Hypothesen bestimmt werden.
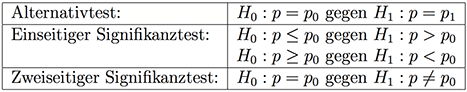
Woran erkennt man, was die $H_0$-Hypothese und was die $H_1$ Hypothese ist? Merke beim Signifikanztest (gilt nicht für Alternativtest):
- In der $H_1$-Hypothese steht niemals ein =, ≤ oder ≥.
- Wenn in der Aufgabe das Wort höchstens (≤) auftaucht, dann wissen wir, dass das die $H_0$-Hypothese kennzeichnet und wir einen rechtsseitigen Hypothesentest durchfu ̈hren.
- Wenn in der Aufgabe das Wort mindestens (≥) auftaucht, dann wissen wir, dass das die $H_0$-Hypothese kennzeichnet und wir einen linksseitigen Hypothesentest durchführen.
- Wenn in der Aufgabe das Wort mehr als oder auch größer (>) auftaucht, dann wissen wir, dass das die $H_1$-Hypothese kennzeichnet und wir einen rechtsseitigen Hypothesentest durchführen.
- Wenn in der Aufgabe das Wort weniger als oder auch weniger (<) auftaucht, dann wissen wir, dass das die $H_1$-Hypothese kennzeichnet und wir einen links- seitigen Hypothesentest durchführen.
Beispiel:
Man möchte durch einen Test nachweisen, dass Berufseinsteiger mit Masterabschluss im Durchschnitt mehr verdienen als Berufseinsteiger mit einem Bachelorabschluss. Dazu befragt man 100 Berufseinsteiger nach ihrem Abschluss und Einstiegsgehalt.
Wie lautet die Null- bzw. Alternativhypothese in diesem Fall?
Lösung:
Da wir nachweisen wollen, dass Berufseinsteiger mit Masterabschluss ein höheres Einstiegsgehalt haben, muss diese Behauptung in die Alternativhypothese. Die Nullhypothese ist das genaue Gegenteil davon. Solange wir keinen Unterschied im Einkommen nachweisen, müssen wir annehmen, dass beide Gruppen dasselbe verdienen:
- $H_0$: Bachelor- und Masterabsolventen bekommen das gleiche Einstiegsgehalt.
- $H_1$: Masterabsolventen bekommen ein höheres Einstiegsgehalt als Bachelorabsolventen.
Mathematisch formuliert: $H_0: \ \mu_M=\mu_B$ und $H_1: \ \mu_M>\mu_B$ mit $\mu_M$ bzw. $\mu_B$ als durchschnittliches Einstiegsgehalt eines Masterstudenten bzw. Bachelorstudenten.
Schau dir zur Vertiefung Daniels Lernvideo zum Thema Hypothesentest an.
Testgröße und Stichprobenlänge
Um entscheiden zu können, welche der beiden Hypothesen angenommen und welche verworfen werden soll, plant man die Durchführung einer Stichprobe. Das heißt, man wiederholt das betreffende Zufallsexperiment $n$-mal unabhängig voneinander. Bei einer Umfrage werden zum Beispiel 100 Leute befragt, ob sie Mathe lieben oder nicht. Die Anzahl der Wiederholungen bezeichnet man als Länge der Stichprobe.
Das, worauf bei der Durchführung der einzelnen Versuche geachtet wird (also die Anzahl der Eintritte des betreffenden Ereignisses), nennt man die Testgröße oder Teststatistik. Sie wird manchmal mit $T$, oft auch mit $X$ oder $Z$ abgekürzt.
Bei der Stichprobe handelt es sich dabei um eine Bernoulli-Kette. Die Testgröße ist daher binomialverteilt.
Beispiel
Um einen Test durchzuführen beauftragt Herr Jung den mit der Bedienung der Videokamera betrauten Mitarbeiter seines Betriebes bei den nächsten 100 von der Kamera gefilmten Lehrvideos darauf zu achten, wie viele davon einen schlechten Ton haben, und ihm das Ergebnis am Ende der Woche mitzuteilen. Was ist in diesem Fall die Stichprobenlänge und was ist bei dieser Stichprobe die Testgröße?
Lösung:
Die Stichprobe hat die Länge $n=100$ und die Testgröße ist die Anzahl der Videos mit schlechtem Ton unter den 100 Videos der Stichprobe.
1,99€
Entscheidungsregel: Annahme- und Ablehnungsbereich
Die Hypothesen sind aufgestellt, die Stichprobe ist durchgeführt und wir haben die Testgröße festgelegt. Um zu einer endgültigen Entscheidung zu kommen, legen wir einen Annahme- und Ablehnungsbereich fest. Abhängig vom Wert, den die Testgröße in der Stichprobe annimmt, wird man die Richtigkeit der einen bzw. der anderen der beiden Hypothesen annehmen.
Der Annahmebereich $A$ umfasst also die Werte zwischen $0$ und $n$, bei denen $H_0$ angenommen werden soll. Im Gegensatz dazu umfasst der Ablehnungsbereich $\bar{A}$ die anderen Werte, bei denen $H_0$ abgelehnt bzw. verworfen werden soll.
Wenn von Entscheidungsregel aufstellen gesprochen wird, sollen für eine der beiden Hypothesen – üblicherweise für die Nullhypothese – Annahme- und Ablehnungsbereich festgelegt werden. Die Entscheidungsregel sollte nicht willkürlich oder nach Gefühl aufgestellt werden. Denn dann kann es passieren, dass Hypothesen zu leicht angenommen oder abgelehnt werden, was die Aussagekraft des Tests verschlechtert. Daher wird vorher ein Signifikanzniveau $\alpha$ festgelegt, dass die Aussagekraft des Tests sichert.
Die folgende Abbildung zeigt uns, wie die Ablehnungs- und Annahmebereiche bei den verschiedenen Testarten aussehen. Für den Ablehnungsbereich bestimmt man zunächst immer den kritischen Wert $k$, der in der Regel abhängig von $\alpha$ ist und gibt dann die Bereiche an. Wie dieser kritische Wert berechnet werden kann, sehen wir in den Kapiteln zu den jeweiligen Testarten.

Achtung: Kommazahlenproblem, runde ich auf oder ab?
Man rundet bei beidseitigen Tests immer nach innen, man spricht auch vom Runden zur sicheren Seite, z.B. $k_l=54,48$ und $k_r=78,92$: $A=[55;78]$. Bei einseitigen Tests muss man darauf achten, ob links- oder rechtsseitig. Zum Beispiel folgt bei einem linksseitigen Test mit $k=9,18$ oder $k=9,88$ der Annahmebereich $A=[10;n]$.
Wahrscheinlichkeiten bestimmen
Beim Testen von Hypothesen möchte man von einer Stichprobe auf die Grundgesamtheit schließen. Aus diesem Grund sollte die Stichprobe möglichst groß gewählt sein, um eine gute Aussage treffen zu können. Da die Testgrößen binomialverteilt sind, müssen wir zur Berechnung von Wahrscheinlichkeiten auf die Binomialverteilung zurückgreifen.
Zur Erinnerung:
\begin{align*}
P(X \leq k)= \sum_{i=0}^k \left( \begin {array} {c} n\\ i \end{array} \right) \cdot p^ i \cdot (1-p)^{n-i}
\end{align*}
Für große Werte von $k$ (typisch bei Hypothesentests) sollte man die Wahrscheinlichkeit nicht mehr per Hand rechnen. Hier lernt ihr zwei Möglichkeiten kennen, wie ihr leicht die jeweiligen Werte bestimmen könnt.
Ablesen aus der $F$-Tabelle
Eine einfache Möglichkeit, wenn man keinen GTR/CAS zur Hand hat oder einfach schneller sein will, ist das Ablesen aus der $F$-Tabelle. Diese Tabelle gibt die aufsummierten Wahrscheinlichkeiten der Binomialverteilung von 0 bis $k$ für verschiedene $n$ und $p$ an und sollte in der Klausur gegeben sein. Es gibt auch eine $B$-Tabelle der Binomialverteilung, die die Wahrscheinlichkeit für genau $k$ Treffer angibt.
Beispiel:
Wird die Wahrscheinlichkeit von $P(X\leq 2)$ mit $n=10$ und $p=0,1$ gesucht, schreiben wir das erstmal in die Form $F(n;p;k)$, also hier $F(10;0,1;2)$ und suchen uns dann die passende $F$-Tabelle für $n=10$ raus. Einen Ausschnitt dieser Tabelle und wie man dann auf den richtigen Wert kommt, seht ihr in der folgenden Abbildung.
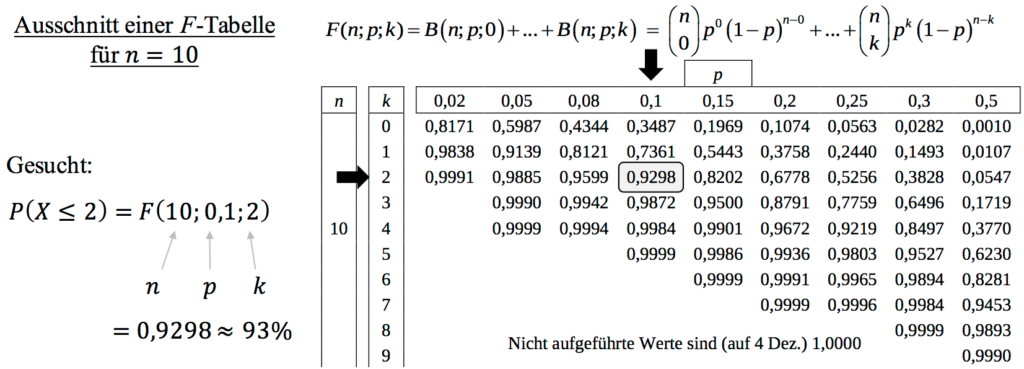
Wichtig: Die gesuchte Wahrscheinlichkeit muss immer auf die Form $\leq$ gebracht werden! Bevor ihr also den Wert für [/latex]\geq[/latex] oder $>$ ablesen könnt, müsst ihr das umschreiben, z.B.:
\begin{align*}
P(X\geq 2)=1-P(X\leq 1) \quad \textrm{oder} \quad P(X > 2)=1-P(X\leq 2)
\end{align*}
Berechnung mit dem GTR/CAS
Wenn ihr mit dem GTR/CAS arbeitet, braucht ihr nur den Befehl: binomcdf$(n,p,k)$! Dieser Befehl berechnet die kumulierten (aufsummierten) Wahrscheinlichkeiten der Binomalverteilung und gibt euch direkt die gesuchte Wahrscheinlichkeit an. Für das Beispiel von oben mit $P(X\leq 2)$, $n=10$ und $p=0,1$ bekommt ihr mit dem Befehl \texttt{binomcdf}$(10;0,1;2)$ direkt den gesuchten Wert.
1,99€
Fehler beim Testen
Eine Hypothese kann nie mit absoluter Sicherheit bestätigt bzw. widerlegt werden, sondern immer nur mit einer gewissen Wahrscheinlichkeit. Das bedeutet, dass jede Entscheidung, die wir basierend auf einer Hypothese treffen, falsch sein kann. Meistens ist der Fehler der, dass wir vorschnell unsere Schlussfolgerung getroffen haben, oder dass wir unvollständige Informationen aus unserer Stichprobe benutzt haben, um damit eine allgemeine Aussage über die Gesamtheit zu treffen.
Denken wir dafür nochmal an das Beispiel mit dem Angeklagten, der schuldig oder unschuldig sein kann. Das Verurteilen eines Unschuldigen ist ein Fehler 1. Art und das Freisprechen eines Schuldigen ein Fehler 2. Art.

Die obige Tabelle zeigt, dass 4 Fälle auftreten können:
a) Wir lehnen $H_0$ ab, also nehmen $H_1$ an.
1. In Wirklichkeit stimmt $H_0$: Hier wird $H_0$ fälschlicherweise abgelehnt. Dieser Fehler wird Fehler 1. Art genannt bzw. $\alpha$-Fehler und beschreibt die Irrtumswahrscheinlichkeit. Die Wahrscheinlichkeit einen Fehler 1. Art zu begehen heißt Signifikanzniveau oder Irrtumswahrscheinlichkeit $\alpha$.
2. In Wirklichkeit stimmt $H_1$, also $H_0$ ist falsch: Alles ist in Ordnung, denn $H_1$ wird angenommen und stimmt tatsächlich. Man spricht von Sicherheit 2. Art.
b) Wir nehmen $H_0$ an.
3. In Wirklichkeit stimmt $H_0$: Alles ist in Ordnung, denn $H_0$ wird angenommen und stimmt tatsächlich. Man spricht von Sicherheit 1. Art.
4. In Wirklichkeit stimmt $H_1$, also $H_0$ ist falsch: Unsere Vermutung ist wahr (d.h. $H_1$, die wir ja nachweisen möchten, stimmt), aber durch den Test konnte sie nicht bestätigt werden, da wir $H_0$ annehmen. Dieser Fehler wird als Fehler 2. Art bzw. $\beta$-Fehler bezeichnet. Diese Wahrscheinlichkeit können wir nicht kontrollieren, sie ist abhängig von der Art des Tests und des Signifikanzniveaus $\alpha$.
Man muss sich vor Durchführung des Tests auf ein Signifikanzniveau $\alpha$ festlegen, das die maximale Wahrscheinlichkeit festlegt, mit der uns so ein Fehler 1. Art passieren darf. Je sicherer wir mit unserer Entscheidung sein wollen, desto niedriger muss diese Fehlerwahrscheinlichkeit gewählt werden. In den allermeisten Fällen, sowohl in der Praxis als auch in Klausuren, ist dieser Wert festgelegt als $\alpha=5$%.
Im Gegensatz zum Fehler 1. Art, lässt sich die Wahrscheinlichkeit für den Fehler 2. Art in der Regel nicht einfach berechnen. Man kann diesen ausschließlich berechnen, wenn man für die Alternativhypothese eine andere Wahrscheinlichkeit als für $H_0$ annimmt.
Im Allgemeinen gilt: Je kleiner die Wahrscheinlichkeiten für einen Fehler der 1. und 2. Art, desto besser.
Wichtig: Man kann $H_0$ nie beweisen, sondern nur $H_1$. Aus diesem Grund ist es wichtig, dass man die Hypothesen richtig herum formuliert: Der Fall, den man nachweisen möchte, kommt in die Alternativhypothese. Die Metapher mit der Gerichtsverhandlung ist eine hilfreiche Eselsbrücke, um sich an dieses Vorgehen zu erinnern.
Beispiel:
In einer Fabrik packt eine Maschine jeweils 100g Schokolade ab.
- $H_0$: $\mu = 100$g (die Maschine arbeitet korrekt)
- $H_1$: $\mu \neq 100$g (die Maschine arbeitet nicht korrekt)
wobei $\mu$ das durchschnittliche Gewicht der Packungen ist.
Betrachten wir nun, welche Fehler bei unseren Hypothesen auftreten können.
1) Bei einem Fehler 1. Art, wird die Nullhypothese ($H_0$) abgelehnt, trotz der Tatsache, dass sie stimmt. Für unser Beispiel würde dies bedeuten, dass die Maschine zwar korrekt arbeiten würde (daher $\mu = 100$g), wir in unserer Stichprobe feststellen würden, dass das Durchschnittsgewicht $\mu \neq 100$g ist.
2) >Beim Fehler 2. Art passiert genau das Gegenteil: die Maschine arbeitet nicht korrekt, sie packt also nicht ein Durchschnittsgewicht von 100g Schokolade ab, unsere Stichprobe zeigt dies allerdings nicht an. Laut ihr arbeitet die Maschine korrekt.
Wir können natürlich auch eine richtige Entscheidung gemäß unserer Stichprobe fällen.
Was passiert aber, wenn unsere Stichprobe aussagt, dass unsere Nullhypothese falsch sei, weil $\mu \neq 100$g ist? Wie wirkt sich das auf den Fehler aus, wenn das Durchschnittsgewicht tatsächlich 100g ist und wenn es nicht 100g ist?
1) Wenn $\mu = 100$g ist, ist die Nullhypothese wahr. Lehnen wir sie ab, begehen wir einen Fehler 1. Art.
2) Wenn $\mu\neq 100$g ist, ist die Nullhypothese falsch. Wenn wir sie ablehnen, treffen wir die richtige Entscheidung.
Alternativtest
Wie wir bereits in der Übersicht kennengelernt haben, gibt es neben den einseitigen und beidseitigen Hypothesentests auch einen Alternativtest. Charakteristisch ist, dass nicht gesagt wird, dass die Nullhypothese sich verringert, erhöht oder verändert hat, sondern, dass eine alternative Aussage gegeben ist. Um das zu verstehen, schauen wir uns das an einem Beispiel an.
Beispiel:
Frau Wanka sagt, dass 10% aller Schüler mit Videos lernen. Daniel ist anderer Meinung und behauptet, dass 30% aller Schüler mit Videos lernen. Sie beschließen, dass wenn mindestens 3 Schüler mit Videos lernen, die Hypothese von Daniel stimmt.
Am Nachmittag fährt Daniel in die Remscheider City und fragt 10 Schüler, ob sie mit Videos lernen.

Schreiben wir uns diese Informationen mal auf:
- Nullhypothese $H_0:\ p_0=0,1$ und Alternativhypothese $H_1:\ p_1=0,3$
- Testgröße $X$: Anzahl der Videolerner; Stichprobe: $n=10$
- Annahmebereich: $A=[0;1;2]$, Ablehnungsbereich: $\bar{A}=[3;4;5;6;7;8;9;10]$
Der Fehler 1. Art wird im Ablehnungsbereich von $H_0$ bestimmt mit der Wahrscheinlichkeit von $H_0$. Die Wahrscheinlichkeit beträgt 7%, dass $H_0$ abgelehnt wird, obwohl $H_0$ tatsächlich stimmt.
Der Fehler 2. Art wird im Annahmebereich von $H_0$ bestimmt mit der Wahrscheinlichkeit von $H_1$. Mit einer 38,3%-igen Wahrscheinlichkeit entscheiden wir uns für $H_0$, obwohl $H_1$ in Wirklichkeit stimmt.
1,99€
Hypothesentest mit δ-Regeln
Die $\sigma$-Regeln beziehen sich auf die Standardnormalverteilung. Sie geben an, wie viel Prozent der Fläche unter der Glockenkurve im Bereich von 1, 2 oder 3 Standardabweichungen links und rechts vom Mittelwert liegt.
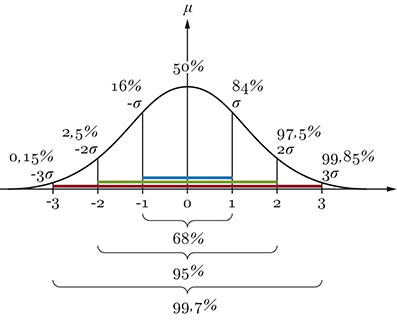
Ungefähr 68% der Werte liegen innerhalb einer Standardabweichung vom Mittelwert. Ebenso liegen ungefähr 95% der Werte innerhalb von zwei Standabweichungen vom Mittelwert. Und ca. 99,7% der Werte befinden sich innerhalb von drei Standardabweichungen vom Mittelwert.
Die Standardabweichung bei der Binomialverteilung berechnet sich wie folgt:
\begin{align*}
X \sim B(n;p): \quad \sigma=\sqrt{n\cdot p \cdot (1-p)}.
\end{align*}
Was hat man davon?
Ist die Streuung groß genug (Laplace-Bedingung: $\sigma > 3$), so lässt sich die entsprechende Binomialverteilung brauchbar durch die Normalverteilung annähern und wir dürfen für den Ablehnungs- und Annahmebereich die $\sigma$-Umgebung verwenden.
Vorgehensweise:
- Hypothesen $H_0$ und $H_1$ aufstellen.
- Entscheiden, ob eins- oder zweiseitiger Hypothesentest vorliegt.
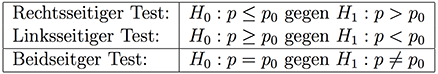
- Erwartungswert berechnen: $\mu= n\cdot p$
- Standardabweichung berechnen: $\sigma=\sqrt{n\cdot p \cdot (1-p)}$
- Vorgegebene Irrtumswahrscheinlichkeit beachten.
![]()
- Entscheidungsregel aufstellen: Annahme- ($A$) und Ablehnungsbereich ($\overline{A}$) mit der $\sigma$-Regel bestimmen
\begin{align*}
\textrm{Zweiseitiger Test:} \quad & A=\left[ \mu – z_{\frac{\alpha}{2}} \cdot \sigma; \ \mu + z_{\frac{\alpha}{2}} \cdot \sigma \right] \\
\textrm{Linksseitiger Test:} \quad & \overline{A}=\left[ 0; \ \mu – z_{\alpha} \cdot \sigma \right] \\
\textrm{Rechtsseitiger Test:} \quad & \overline{A}=\left[ \mu + z_{\alpha} \cdot \sigma; \ n \right]
\end{align*}
In der Entscheidungsregel werden durch Vorgabe eines Signifikanzniveaus Ablehnungsbereich und Annahmebereich festgelegt. Das Signifikanzniveau ist dabei die Gegenwahrscheinlichkeit zur Sicherheitswahrscheinlichkeit.
- Testentscheidung anhand der gegebenen Stichprobe $n$.
- Fehler 1. Art berechnen und im Sachzusammenhang beschreiben.
- Fehler 2. Art berechnen und im Sachzusammenhang beschreiben.
1,99€
Beidseitiger Hypothesentest:
Beim zwei- bzw. beidsetigen Hypothesentest lauten die Hypothesen allgemein
\begin{align*}
H_0:~p=p_0; \quad H_1: ~p \neq p_0.
\end{align*}
Wichtig: Bei einem beidseitigen Hypothesentest werden sowohl die linke als auch die rechte Seite hinsichtlich des Ablehnungsbereichs betrachtet. Wenn in Summe 10% abgelehnt werden sollen, müssen diese Prozente auf den linken und rechten Bereich aufgeteilt werden. Was das bedeutet sehen wir im folgenden Beispiel, wenn das Signifikanzniveau $\alpha=5$% lauten würde.

Beispiel zum beidseitigen Hypothesentest:
Es werden Fußballfans in einer Stadt betrachtet. Dabei machen 20% die Fans einer Mannschaft A aus B. Wir nehmen nun eine Stichprobe von 158 Fußballfans (Signifikanzniveau: 5%).
In der Stichprobe befinden sich 43 Fußballfans der Mannschaft A und 115 der Mannschaft B.
Kann $H_0$ verworfen werden?
Berechne zudem die Wahrscheinlichkeit für den Fehler 1. und 2. Art, wenn der tatsächliche Anteil der Fußballfans 30% beträgt.
Wir arbeiten hierfür das allgemeine Vorgehen ab:
- Man stellt zunächst Hypothesen auf.
\begin{align*}
H_0:~ p =0,2;~ H_1:~ p \neq 0,2
\end{align*} - Wir erkennen, dass es sich hierbei um einen zweiseitigen Hypothesentest handelt.
- Erwartungswert/Punktschätzung berechnen:
\begin{align*}
\mu=n\cdot p = 158\cdot 0,2= 31,6
\end{align*} - Standardabweichung berechnen und Laplace-Bedingung prüfen:
\begin{align*}
\sigma=\sqrt{n\cdot p \cdot (1-p)}= \sqrt{158 \cdot 0,2 \cdot (1-0,2)}=5,03 > 3 \quad
\end{align*} - Vorgegebenes Signifikanzniveau beachten:
- $\alpha=0,05$ als Irrtumswahrscheinlichkeit
- $1-\alpha=0,95$ als Sicherheitswahrscheinlichkeit
- $z_{\frac{\alpha}{2}}$, da ein zweiseitiger Hypothesentest vorliegt
Diesen Wert können wir in den Quantilen der Standardnormalverteilung ablesen.
- Annahme- und Ablehnungsbereich mit den $\sigma$-Regeln bestimmen:
\begin{align*}A=\left[ \mu – z_{\frac{\alpha}{2}} \cdot \sigma, \mu + z_{\frac{\alpha}{2}} \cdot \sigma \right]\end{align*}mit $\sigma=5,03$, $\mu=31,6$ und $z_{\frac{\alpha}{2}}=1,96$ folgt\begin{align*}A= \left[ 31,6 – 1,96 \cdot 5,03; \ 31,6 + 1,96 \cdot 5,03 \right] = \left[ 22; 41 \right].\end{align*}Der Ablehnungsbereich lautet demnach $\overline{A}= \left[ 0; 21 \right] \cup \left[ 42; 158 \right]$. - Entscheidungsregel aufstellen:
$H_0$ wird verworfen, wenn höchstens 21 oder mindestens 42 Personen Fußballfans der Mannschaft A sind. Graphisch können wir uns die Entscheidungsregel auch folgendermaßen vorstellen.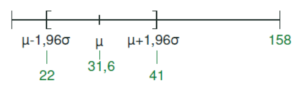
- Testentscheidung anhand der gegebenen Stichprobe $n$: In der Aufgabe steht, dass sich in der Stichprobe 43 Fußballfans befinden, was bedeutet, dass dieser Wert nicht in den Annahmebereich fällt, sondern in den Ablehnungsbereich, der sich rechts und links des Annahmebereichs $[22;41]$ befindet.
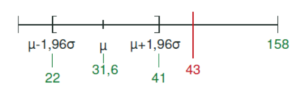 Die Stichprobe liefert das Ergebnis, dass $H_0$ verworfen werden kann, da 43 Fußballfans der Mannschaft A im Ablehnungsbereich liegt.
Die Stichprobe liefert das Ergebnis, dass $H_0$ verworfen werden kann, da 43 Fußballfans der Mannschaft A im Ablehnungsbereich liegt. - Fehler 1. Art und 2. Art: Jemand behauptet, dass der tatsächliche Anteil Fußball Fans bei 30% liegt, also liegt hier ein Alternativtest vor und wir können den Fehler 1. und 2. Art berechnen. Im Sachzusammenhang beschreibt der Fehler 1. Art die Wahrscheinlichkeit, dass die Hypothese „20% der Fußballfans sind Anhänger von Mannschaft A“ verworfen wird, obwohl sie richtig ist. Diese war im Aufgabentext gegeben und beträgt $\alpha=5$%.Der Fehler 2. Art bedeutet, dass eine Hypothese angenommen wird obwohl diese falsch ist. Die Berechnung erfolgt über\begin{align*}P(22 \leq X \leq 41)=F(158;0,3;41)- F(158;0,3;21)\end{align*}und kann mit dem Taschenrechner oder mit der Tabelle gelöst werden. Da es keine Tabelle für $n=158$ gibt und die Laplace-Bedingung erfüllt ist, können wir die Binomialverteilung durch die Normalverteilung approximieren. Da eine Approximation von der Binomialverteilung (diskret) zur Normalverteilung (stetig) vorliegt, müssen Stetigkeitskorrekturen beachtet werden. Es folgt:\begin{align*}P(a \leq X \leq b) &\approx \Phi \left( \frac{b+0,5-np}{\sqrt{np(1-p)}} \right)- \Phi \left( \frac{a-0,5-np}{\sqrt{np(1-p)}} \right) \\ \\\Rightarrow \quad P(22 \leq X \leq 41) &\approx \Phi \left( \frac{41+0,5-47,4}{\sqrt{5,76}} \right) – \Phi \left( \frac{22-0,5-47,4}{\sqrt{5,76}} \right) \\ \\&= \Phi(-1,02)-\Phi(-4,5) \\&= 1- \Phi(1,02)- ( 1 – \Phi(4,5)) \\&=0,1539 \approx 15,39\%\end{align*}Zu 15,39% wird die $H_0$ Hypothese angenommen, obwohl diese falsch ist. Das heißt, dass zu 15,39% angenommen wird, dass der Anteil der Fußballfans 20% beträgt, obwohl dies nicht der Wahrheit entspricht.
1,99€
Einseitiger Hypothesentest
Wenn es bei einem Hypothesentest lediglich darum geht, ob sich die Wahrscheinlichkeit eines Ereignisses in eine Richtung geändert hat, handelt es sich um einen einseitigen Hypothesentest.
Wenn man vermutet, dass die Wahrscheinlichkeit kleiner ist als bislang angenommen, spricht man von einem linksseitigen Hypothesentest bzw. Signifikanztest.
Vermutet man eine größere Wahrscheinlichkeit des Ereignisses, spricht man von einem rechtsseitigen Signifikanztest.
Linksseitiger Hypothesentest
Bei einem linksseitigen Hypothesentest sprechen kleine Werte der Zufallsvariablen gegen die Hypothese, also Werte, die links auf dem Zahlenstrahl bzw. links vom Erwartungswert liegen.
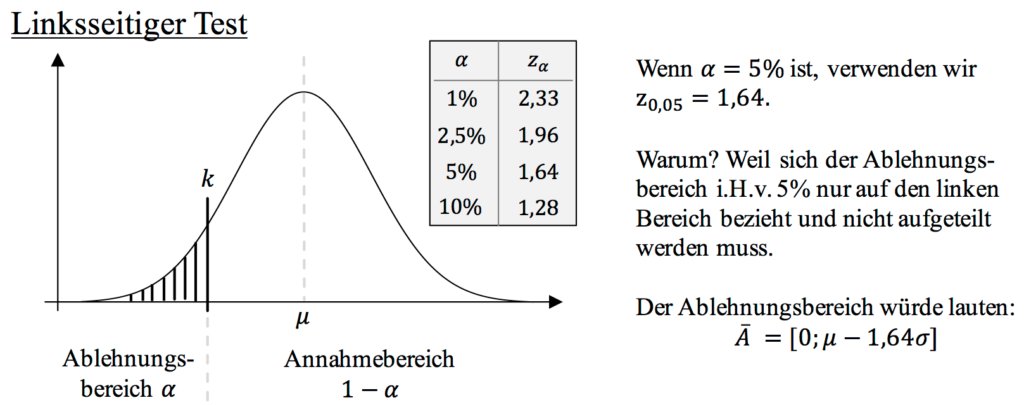
Beispiel zum linksseitigen Hypothesentest:
Bei der letzten Wahl hat ein Kandidat 40% der abgegebenen Stimmen erhalten. Um zu prüfen, ob er seinen Stimmenanteil zumindest gehalten hat, wird einige Zeit vor der nächsten Wahl eine Umfrage durchgeführt. Von 100 Personen geben nur 34 an, dass sie diesen Kandidaten wählen werden. Kann man hieraus mit der Irrtumswahrscheinlichkeit 5% schließen, dass der Stimmenanteil des Kandidaten gesunken ist?
- Hypothesen aufstellen:
\begin{align*}
H_0:~ p \geq 0,4; ~ H_1: p < 0,4
\end{align*}
Text genau lesen! “mindestens 40% der Stimmen erhalten…” Das wäre gut und ist daher unsere Nullhypothese. - Wir erkennen, dass es sich hierbei um einen einseitigen Hypothesentest handelt.Linksseitiger Hypothesentest, da sehr kleine Werte gegen $H_0$ sprechen.
- Erwartungswert/Punktschätzung berechnen:
\begin{align*}
\mu= n\cdot p = 100 \cdot 0,4 =40
\end{align*} - Standardabweichung berechnen und Laplace-Bedingung prüfen:
\begin{align*}\sigma= \sqrt{n\cdot p\cdot (1-p)} = \sqrt{100 \cdot 0,4\cdot (1-0,4)}=4,898 > 3 \quad \end{align*} - Signifikanzniveau beachten:
- $\alpha=0,05$ als Irrtumswahrscheinlichkeit
- $1-\alpha=0,95$ als Sicherheitswahrscheinlichkeit
- $z_{\alpha}$, da ein einseitiger Hypothesentest vorliegt
Diesen Wert können wir in den Quantilen der Standardnormalverteilung ablesen.
- Annahme- und Ablehnungsbereich mit den $\sigma$-Regeln bestimmen. Allgemein gilt:
\begin{align*}
\left[ \mu – z_\alpha \cdot \sigma \right]
\end{align*}Den Erwartungswert und die Standardabweichung kennen wir. Aus den Quantilen der Standardnormalverteilung folgt für $z_\alpha=1,6449$. Einsetzen und wir bekommen (abgerundet, da linksseitig) den Ablehnungs- und Annahmebereich:\begin{align*}\overline{A}=\left[ 0; 31\right] \quad \textrm{und} \quad A=\left[32; 100 \right]\end{align*} - Entscheidungsregel aufstellen: $H_0$ wird verworfen, wenn höchstens 31 Personen den Kandidaten wählen.
- Testentscheidung anhand der gegebenen Stichprobe $n$:In der Aufgabe steht, dass 34 Personen angaben, dass sie den Kandidaten wählen werden. Die Stichprobe liefert das Ergebnis, dass $H_0$ nicht verworfen werden kann, also beibehalten wird, da sich der Wert der Stichprobe im Annahmebereich befindet und nicht im Ablehnungsbereich.
- Fehler 1. Art definieren und im Folgenden berechnen/beschreiben im Sachzusammenhang: Der Fehler 1. Art bedeutet, dass eine wahre Hypothese verworfen wird und diesen kann man Signifikanzniveau/Irrtumswahrscheinlichkeit, hier 5% ablesen. Das heißt, dass die $H_0$-Hypothese zu 5% irrtümlich abgelehnt wird.
Rechtsseitiger Hypothesentest
Bei einem rechtsseitigen Hypothesentest sprechen große Werte der Zufallsvariablen gegen die Hypothese, also Werte, die rechts auf dem Zahlenstrahl bzw. rechts vom Erwartungswert liegen.
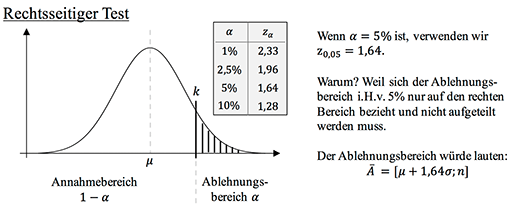
1,99€
Beispiel zum rechtsseitigen Hypothesentest:
In einer Limonaden-Fabrik werden Flaschen abgefüllt und verschlossen. Dabei werden nicht alle Flaschen ordnungsgemäß verschlossen. Stündlich werden 100 Flaschen kontrolliert. Erfahrungsgemäß werden nicht mehr als 20% der Flaschen falsch verschlossen. In einer Stichprobe werden 25 Flaschen gefunden, die falsch verschlossen sind.
1) Wie viele falsch verschlossene Flaschen dürfen höchstens in der Kontrolle gefunden werden? (Irrtumswahrscheinlichkeit = 5%)
2) Berechne den Fehler 2. Art, wenn tatsächlich 20% der Flaschen falsch verschlossen werden.
Zur Lösung der Aufgabe arbeiten wir das bekannte Vorgehen ab:
- Hypothesen aufstellen:
\begin{align*}
H_0:~ p \leq 0,2; ~ H_1: p > 0,2
\end{align*}
Text genau lesen! “höchstens 20% der Flaschen falsch verschlossen…” ist unsere Nullhypothese. - Wir erkennen, dass es sich hierbei um einen einseitigen Hypothesentest handelt, da hohe Werte gegen $H_0$ sprechen.
- Erwartungswert/Punktschätzung berechnen:
\begin{align*}
\mu= n\cdot p = 100 \cdot 0,2 =20
\end{align*} - Standardabweichung berechnen und Laplace-Bedingung prüfen:
\begin{align*}\sigma= \sqrt{n\cdot p\cdot (1-p)} = \sqrt{100 \cdot 0,2\cdot (1-0,2)}=4>3 \quad \end{align*} - Signifikanzniveau beachten:
- $\alpha=0,05$ als Irrtumswahrscheinlichkeit
- $1-\alpha=0,95$ als Sicherheitswahrscheinlichkeit
- $z_{\alpha}$, da ein einseitiger Hypothesentest vorliegt
Diesen Wert können wir in den Quantilen der Standardnormalverteilung ablesen.
- Annahme- und Ablehnungsbereich mit den $\sigma$-Regeln bestimmen. Allgemein gilt:
\begin{align*}
\left[ \mu + z_\alpha \cdot \sigma \right]
\end{align*}Den Erwartungswert und die Standardabweichung kennen wir. Aus den Quantilen der Standardnormalverteilung folgt für $z_\alpha=1,6449$. Einsetzen und wir bekommen (aufgerundet, da rechtsseitig) den Ablehnungs- und Annahmebereich:\begin{align*}\overline{A}=\left[27; 100 \right] \quad \textrm{und} \quad A=\left[ 0; 26 \right].\end{align*} - Entscheidungsregel aufstellen: $H_0$ wird verworfen, wenn mehr als 26 Flaschen falsch verschlossen sind.
- Testentscheidung anhand der gegebenen Stichprobe $n$:In der Aufgabe steht, dass in der Stichprobe 25 Flaschen gefunden worden sind, die falsch verschlossen waren. Das bedeutet, dass dieser Wert in den Annahmebereich fällt. Die Stichprobe liefert das Ergebnis, dass $H_0$ nicht verworfen werden kann, also beibehalten wird, da sich der Wert der Stichprobe im Annahmebereich befindet.
- Fehler 1. Art definieren und im Folgenden berechnen/beschreiben im Sachzusammenhang:Der Fehler 1. Art bedeutet, dass eine wahre Hypothese verworfen wird und diesen man am Signifikanzniveau ablesen kann. Das heißt, dass die $H_0$ Hypothese zu 5% irrtümlich abgelehnt wird.
- Fehler 2. Art berechnen und im Sachzusammenhang beschreiben:Der Fehler 2. Art bedeutet, dass eine Hypothese angenommen wird obwohl diese in Wirklichkeit falsch ist. Wir berechnen den Fehler 2. Art wie gewohnt:\begin{align*}\beta&= P( X \leq 26) \approx \Phi \left( \frac{26+0,5-100\cdot 0,3}{\sqrt{100\cdot 0,3 \cdot (1-0,3)}} \right) = \Phi(-0,7637) \\&= 1- \Phi( 0,76) =1-0,7764 \approx 22,36\%\end{align*}Der Test fällt zu 22,36% in den Annahmebereich, obwohl mehr als 20% (nämlich 30%) falsch verschlossene Flaschen in der Stichprobe zu finden sind.
1,99€
Hypothesentest mit Ablesen aus Tabelle
Falls ihr, aus welchem Grund auch immer, die $\sigma$-Regeln nicht verwenden dürft, gibt es noch die Möglichkeit Hypothesentests mit Hilfe von Tabellen zu bearbeiten. Was ihr in diesem Kapitel also bereits können solltet ist das Ablesen von Werten in der $F$-Tabelle bzw. falls ihr diese Tabellen selbst mit eurem GTR/CAS erzeugen müsst, wie man sie mit Hilfe des Befehls binomcdf anzeigen lassen kann. Wir gehen jetzt nur auf das reine Ablesen aus der Tabelle ein, da es im Grunde genommen genau das Gleiche ist, wie wenn ihr sie vorher mit dem Taschenrechner erzeugt.
Wo liegt der Unterschied zum Umgang mit den $\sigma$-Regeln? Beim Aufstellen der Entscheidungsregel, also wie der Annahme- und Ablehnungsbereich bestimmt wird. Das ist hier etwas umständlicher. Der restliche Ablauf ist identisch.
Linksseitiger Hypothesentest
Vorgehensweise:
1. Hypothesen aufstellen: $H_0: p \geq p_0; \ H_1: p < p_0$
2. Festlegung des Stichprobenumfangs $n$ und des Siginifikanzniveaus $\alpha$
3. Bestimmung des Ablehnungsbereiches: $\overline{A}=[0; k]$
Es muss gelten: $P(X\leq k) \leq \alpha$
4. Entscheidungsregel: Liegt der Stichprobenumfang in $\overline{A}$, wird $H_0$ verworfen, ansonsten wird $H_0$ beibehalten.
Beispiel
Es wird behauptet, dass mindestens 30% der Schüler bei ihrer Mathe-Abi-Klausur spicken. Um diese These zu überprüfen, werden 100 Schüler einer Schule befragt. Das Signifikanzniveau beträgt $\alpha = 5$%. Leite eine Entscheidungsregel her.
Zunächst stellen wir die Hypothesen auf. Das Signalwort im Aufgabentext ist mindestens, so dass wir direkt wissen, dass die Hypothesen wie folgt lauten:
\begin{align*}
H_0: p_0 \geq 0,3; \quad \textrm{und} \quad H_1: p_1 < 0,3
\end{align*}
Aus dem Aufgabentext können wir ebenfalls entnehmen, dass der Stichprobenumfang $n=100$ ist und das Signifikanzniveau bei 5% liegt. Die Irrtumswahrscheinlichkeit ist sehr wichtig, denn sie legt den kritischen Wert fest, ab wann wir die Nullhypothese annehmen. Zur Veranschaulichung ist die Funktion der Binomialverteilung nochmal grafisch dargestellt.
Es gilt jetzt also den kritischen Wert mit Hilfe der passenden $F$-Tabelle (das war die mit den kumulierten Wahrscheinlichkeiten) zu bestimmen. Der passende Ausschnitt, den ihr in der Klausur selbst heraussuchen müsst, ist ebenfalls dargestellt.
Er zeigt die $F$-Tabelle für $n=100$ für die Wahrscheinlichkeit $p=0,3$.
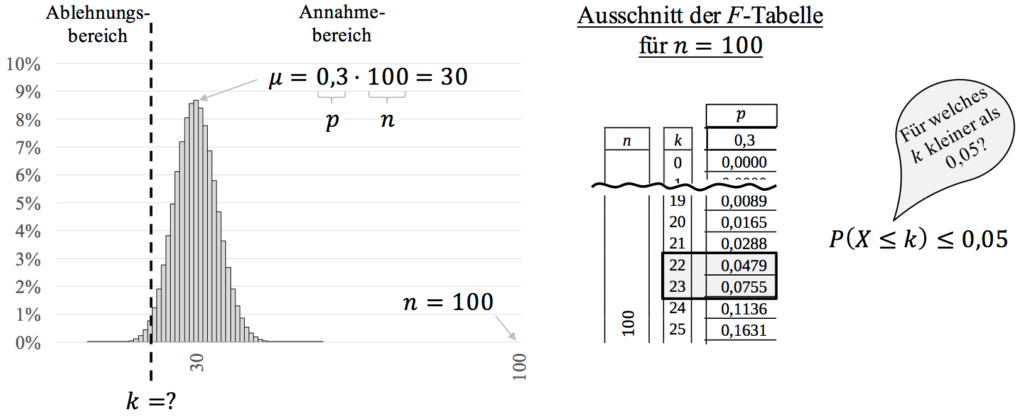
Folgende Bedingung gilt für den Ablehnungsbereich: $P(X \leq k) \leq \underbrace{0,05}_{\alpha}$.
Wir suchen in der Tabelle jetzt die Wahrscheinlichkeit, die gerade kleiner oder gleich der Irrtumswahrscheinlichkeit i.H.v. 0,05 ist. Wir sehen, dass für $k=22$ der Wert gerade noch unter 0,05 ist, aber bei $k=23$ wird der Wert schon überstiegen.
Ihr könnt in der Klausur dann schreiben:
\begin{align*}
P(X \leq k) = \ &F(100;~0,3~;k) \leq 0,05 \notag \\
&F(100;~0,3~;22) = 0,0479 \leq 0,05 \quad \notag \\
&F(100;~0,3~;23) = 0,0755 > 0,05 \quad \notag
\end{align*}
Wir nehmen für den kritischen Wert den Wert, der so gerade unterhalb von 0,05 liegt. Daraus folgt für den Ablehnungs- und Annahmebereich:
\begin{align*}
\overline{A}=[0 ; 22] \quad \textrm{und} \quad A=[23 ; 100]
\end{align*}
Denkt daran, die Entscheidungsregeln aufzustellen und auszuformulieren! Wenn von insgesamt 100 Schülern höchstens 22 sagen, dass sie spicken, dann wird die Nullhypothese verworfen.
Wenn insgesamt 23 oder mehr Schüler sagen, dass sie spicken, dann wird die $H_0$-Hypothese beibehalten.
1,99€
Rechtsseitiger Hypothesentest
Vorgehensweise:
1. Hypothesen aufstellen: $H_0: p \leq p_0; \ H_1: p > p_0$
2. Festlegung des Stichprobenumfangs $n$ und des Siginifikanzniveaus $\alpha$
3. Bestimmung des Ablehnungsbereiches: $\overline{A}=[k; n]$
Es muss gelten: $P(X\geq k) \leq \alpha \Leftrightarrow 1- P(X\leq k-1) \leq \alpha$.
4. Entscheidungsregel: Liegt der Stichprobenumfang in $\overline{A}$, wird $H_0$ verworfen, ansonsten wird $H_0$ beibehalten.
Beispiel:
Es wird behauptet, dass höchstens 30% der Schüler bei ihrer Mathe-Abi-Klausur spicken. Um diese These zu überprüfen, werden 100 Schüler einer Schule befragt. Das Signifikanzniveau beträgt $\alpha = 5$%. Leite eine Entscheidungsregel her.
Zunächst stellen wir die Hypothesen auf. Das Signalwort im Aufgabentext ist höchstens, so dass wir direkt wissen, dass die Hypothesen wie folgt lauten:
\begin{align*}
H_0: p_0 \leq 0,3; \quad \textrm{und} \quad H_1: p_1 > 0,3
\end{align*}
Aus dem Aufgabentext können wir noch entnehmen, dass der Stichprobenumfang $n=100$ ist und das Signifikanzniveau bei 5% liegt. Die Irrtungswahrscheinlichkeit ist sehr wichtig, denn sie legt den kritischen Wert fest, ab wann wir die Nullhypothese annehmen.
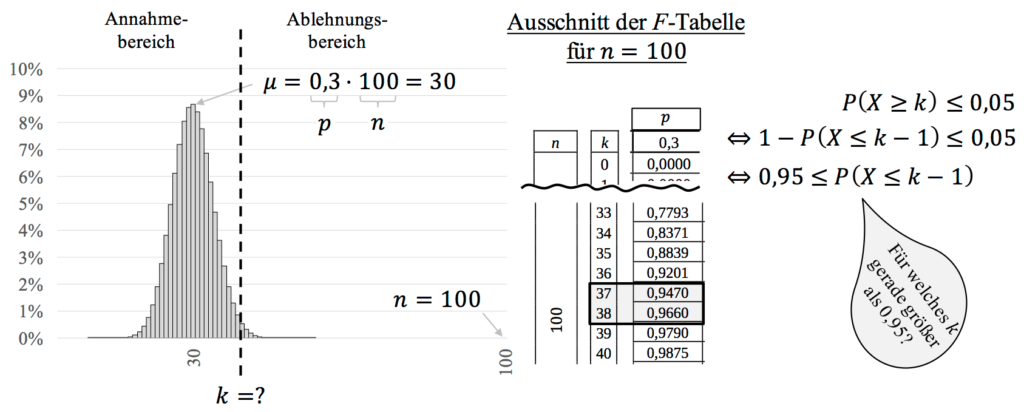
Zur Veranschaulichung ist die Funktion der Binomialverteilung nochmal grafisch dargestellt. Es gilt jetzt also den kritischen Wert mit Hilfe der $F$-Tabelle (das war die mit den kumulierten Wahrscheinlichkeiten) zu bestimmen. Der passende Ausschnitt, den ihr in der Klausur selbst heraussuchen müsst, ist ebenfalls dargestellt. Dieser zeigt die $F$-Tabelle für $n=100$ und $p=0,3$.
Im Gegensatz zum linksseitigen Hypothesentest müssen wir beim Festlegen des Ablehnungsbereichs etwas aufpassen, denn die Bedingung
\begin{align*}
P(X\geq k)\leq \underbrace{0,05}_{\alpha}
\end{align*}
muss zunächst mit der Gegenwahrscheinlichkeit umgeschrieben werden. Warum? Weil wir nur mit Tabellen arbeiten, die die Wahrscheinlichkeiten von 0 bis $k$ summieren und nicht von $k$ bis $n$.
Daher folgt aus der Bedingung:
\begin{align*}
P(X\geq k)\leq 0,05 \ \Leftrightarrow \ 1-P(X\leq k-1)\leq 0,05 \ \Leftrightarrow \ 0,95 \leq P(X\leq k-1)
\end{align*}
Wir suchen in der entsprechenden $F$-Tabelle den Wert, der gerade größer oder gleich 0,95 ist. Für $k=37$ liegen wir gerade noch unter 0,95, aber bei $k=38$ wird der Wert von 0,95 erstmalig überschritten. Das ist der Wert, mit dem wir gleich den Ablehnungsbereich bestimmen. Mathematisch könnt ihr das in der Klausur wiefolgt aufschreiben:
\begin{align*}
0,95 &\leq P(X\leq k-1) \\
0,95 &\leq F(100;~0,3~;k -1) \\
0,95 &\leq F(100;~0,3~;37) = 0,947 \quad \\
0,95 &\leq F(100;~0,3~;\underbrace{38}_{=k-1}) = 0,966 \quad \notag
\end{align*}
Wir nehmen für den kritischen Wert den Wert, der so gerade oberhalb von 0,95 liegt. Jetzt müssen wir noch kurz aufpassen, denn der kritische Wert ist $k-1=38$, also $k=39$.
Damit folgt für den Ablehnungs- und Annahmebereich:
\begin{align*}
\overline{A}=[39; 100] \quad \textrm{und} \quad A=[0; 38].
\end{align*}
Denkt daran, die Entscheidungsregeln aufzustellen und auszuformulieren! Wenn von insgesamt 100 Schülern mindestens 39 sagen, dass sie spicken, dann wird die Nullhypothese verworfen.
Wenn insgesamt 38 oder weniger Schüler sagen, dass sie spicken, dann können wir die $H_0$-Hypothese bestätigen.
1,99€
Beidseitiger Hypothesentest
Vorgehensweise:
1. Hypothesen aufstellen: $H_0: p= p_0; \ H_1: p \neq p_0$
2. Festlegung des Stichprobenumfangs $n$ und des Siginifikanzniveaus $\alpha$
3. Bestimmung des Ablehnungsbereiches: $\overline{A}=[0;k_l] \cup [k_r; n]$
Es muss gelten: $P(X\leq k_l) \leq \alpha/2$ und $P(X\geq k_r) \leq \alpha/2$.
4. Entscheidungsregel: Liegt der Stichprobenumfang in $\overline{A}$, wird $H_0$ verworfen, ansonsten wird $H_0$ beibehalten.
Beispiel:
Es wird behauptet, dass sich die Quote, dass 30% der Schüler bei ihrer Mathe-Abi-Klausur spicken, geändert hat. Um diese These zu überprüfen, werden 100 Schüler einer Schule befragt. Das Signifikanzniveau beträgt $\alpha = 5$%. Leite eine Entscheidungsregel her.
Zunächst stellen wir die Hypothesen auf. Das Signalwort im Aufgabentext ist geändert, so dass wir direkt wissen, dass die Hypothesen wie folgt lauten:
\begin{align}
H_0: p_0 = 0,3 \quad \textrm{und} \quad H_1: p_1 \neq 0,3 \notag
\end{align}
Die restlichen Abläufe sind wie bei dem einseitigen Test. Wir machen quasi einen links- und rechtsseitigen Test in Einem. Einziger Unterschied: Wir müssen beim Signifikanzniveau $\alpha$ aufpassen, da es auf die beiden Ablehnungsbereiche aufgeteilt wird. Die Verteilung ist in der folgenden Abbildung mit den entsprechenden Ausschnitten der $F$-Tabelle dargestellt.
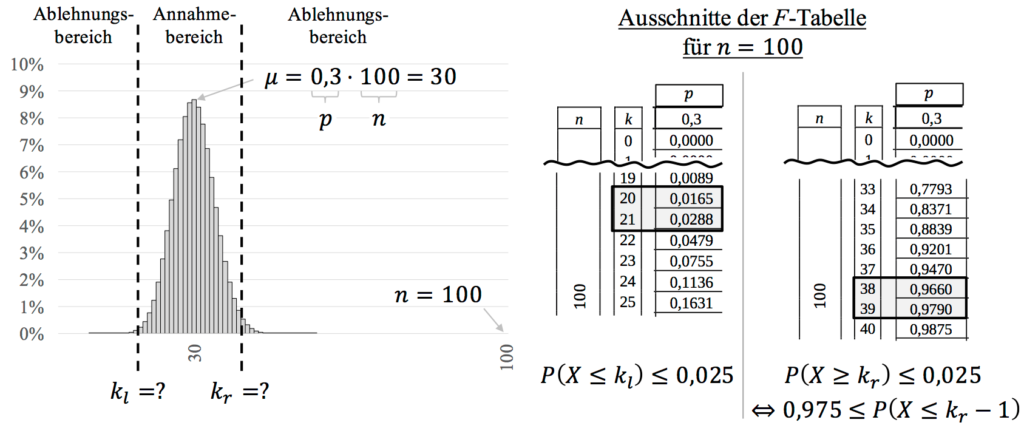
Aus den Bedingungen folgt für die kritischen Werte des Ablehnungsbereichs:
\begin{align*}
F(100;~0,3~;k_l) &\leq 0,025 \notag \\
F(100;~0,3~;20) &= 0,0165 \leq 0,025 \quad \notag \\
F(100;~0,3~;21) &= 0,0288 > 0,025 \quad \notag
\end{align*}
\begin{align*}
0,975 &\leq F(100;~0,3~;k_r-1) \notag \\
0,975 &\leq F(100;~0,3~;38) = 0,966 \quad \notag \\
0,975 &\leq F(100;~0,3~;\underbrace{39}_{k_r-1}) = 0,979 \quad \notag
\end{align*}
Wir nehmen für den kritischen Wert $k_r$ den Wert, der so gerade oberhalb von 0,975 liegt. Jetzt müssen wir noch kurz aufpassen, denn der kritische Wert ist $k_r-1=39$, also $k_r=40$. Damit folgt für den Ablehnungs- und Annahmebereich:
\begin{align*}
\overline{A}=[0; 20] \cup [40; 100] \quad \textrm{und} \quad A=[21; 39]
\end{align*}
Wenn von insgesamt 100 Schülern höchstens 20 und mindestens 40 angeben, sie spicken in der Abi-Klausur, dann würde die Hypothese abgelehnt werden. Wenn im Bereich 21 bis 39 Schüler angeben, dass sie in der Klausur spicken, dann wird die Hypothese bestätigt und wir bleiben dabei.
1,99€
