
Ableiten
In diesem Artikel erklären wir euch schnell und leicht verständlich die Grundlagen fürs Ableiten von Funktionen.
Inhalt auf dieser Seite
- Überblick wichtiger Ableitungsregeln
- Warum bilden wir eine Ableitung?
- Grundlagen zum Ableiten
- Grafisches Ableiten und Aufleiten
- Kettenregel
- Produkteregel
- Quotientenregel
- Weitere Ableitungsregeln
- e- und ln-Funktion ableiten
Neu!
Überblick wichtiger Ableitungsregeln

Warum bilden wir eine Ableitung?
Im Kapitel Kurvendiskussion werden wir sehen, dass die erste Ableitung zum Beispiel ein notwendiges Kriterium zum Vorliegen von Extremwerten ist. Denn wenn die Tangentensteigung an einer Stelle gleich 0 ist, also $f'(x_0)=0$, wissen wir, dass an der Stelle $x_0$ (können auch mehrere Stellen sein) ein Hoch- oder Tiefpunkt (oder Sattelpunkt) vorliegt.
Bevor wir uns jetzt die ganzen Ableitungsregeln anschauen, sollen die Zusammenhänge der Ableitungen untereinander verständlich gemacht werden. Wie diese zusammenhängen sehen wir im nachfolgenden Abschnitt.
Grundlagen zum Ableiten
Was du zunächst zum Thema Ableiten wissen solltets: Geometrisch entspricht die Ableitung einer Funktion der Tangentensteigung. Wie du dir das vorstellen kannst, sehen wir in der Abbildung.
Angenommen die Funktion lautet $f(x)=x^2$, dann lautet die zugehörige erste Ableitung $f'(x)=2x$, welche die Steigung der Tangente an jeder Stelle $x_0$ definiert.
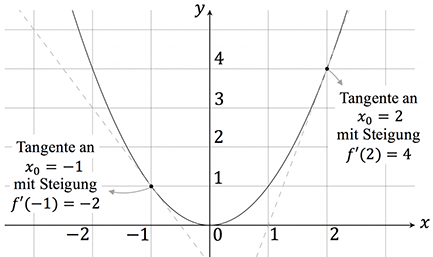
Setzen wir für $x$ Zahlen ein, z.B. $x_0=2$, sehen wir, dass die Tangentensteigung an der Stelle 2 gleich $f'(2)=4$ ist. Wenn wir $x_0=-1$ einsetzen, erhalten wir mit $f'(-1)=-2$ die Steigung der Tangente an der Stelle -1.
Es gilt (was sich leicht aus der obigen Grafik nachvollziehen lässt):
- liegt $x_0$ in einem Bereich, in dem die Kurve steigt, gilt $f'(x)>0$
- liegt $x_0$ in einem Bereich, in dem die Kurve fällt, gilt $f'(x)<0$
Neu!
Grafisches Ableiten und Aufleiten
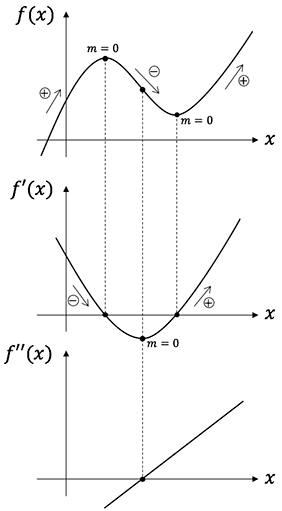
Anhand der folgenden Grafik kann man schön sehen, wie $f(x), f'(x)$ und $f“(x)$ miteinander verbunden sind. Vielleicht kennt ihr diese Eselsbrücke: N steht hierbei für die Nullstelle, E für Extrempunkt und W für den Wendepunkt.
\begin{align*}
\begin{array}{|c|c|c|c|c|c}
f(x) & N & E & W & & \\
f'(x) & & N & E & W & \\
f“(x) & & & N & E & W
\end{array}
\end{align*}
Was soll uns diese Tabelle sagen?
Die Tabelle zeigt zusammenfassend, welche Funktion uns welchen Wert für die jeweilige Ableitung oder Aufleitung liefert.
Gucken wir uns dazu die Abbildung etwas genauer an:
Die Nullstelle der 2. Ableitung $f“(x)$ zeigt uns den $x$-Wert für den Extrempunkt der 1. Ableitung $f'(x)$. Dieser wiederum zeigt uns, wo die Ausgangsfunktion $f(x)$ seinen Wendepunkt hat.
Daniel erklärt dir nochmal in seinem Lernvideo wie man graphisch ableitet!
Kettenregel
Wie der Name schon sagt, muss die Kettenregel immer dann angewendet werden, wenn wir zwei miteinander verkettete Funktionen vorliegen haben. Man spricht dann von einer inneren und von einer äußeren Funktion. Im Allgemeinen hat eine solche Funktion die folgende Form:
\begin{align*}
f(x)&=g(h(x))
\end{align*}
Schauen wir uns dazu ein einfaches Beispiel an:
\begin{align*}
f(x)&=(x^3+2)^2
\end{align*}
Jetzt versuchen wir die innere und die äußere Funktion zu identifizieren. Die äußere Funktion ist $g(h)=h^2$ und die innere Funktion lautet $h(x)=x^3+2$.
Wenn wir diese Funktion nun ableiten müssen, kommt die folgenden Regel zum Tragen:
\begin{align*}
f(x)&=g(h(x))\rightarrow h'(x)\cdot g'(h(x))
\end{align*}
Einfacher formuliert kann man sagen, innere Ableitung multipliziert mit der äußeren Ableitung. Wenn wir diese Regel jetzt auf unser Beispiel anwenden, erhalten wir die folgende Ableitungsfunktion:
\begin{align*}
f'(x)&=3x^2 \ \cdot 2 \cdot(x^3+2)
\end{align*}
An dieser Stelle können wir unsere Ableitungsfunktion noch etwas vereinfachen:
\begin{align*}
f'(x)&=6x^2\cdot (x^3+2)
\end{align*}
Weiteres Beispiel Ableiten mit Kettenregel
\begin{align*}
f(x)= (x^3+5x)^3
\end{align*}
mit $u(v)=v^3 \rightarrow u'(v)=3v^2$ und $v(x)=x^3+5x \rightarrow v'(x)= 3x^2+5$ lautet die erste Ableitung:
\begin{align*}
f'(x)= 3\cdot (x^3+5x)^2\cdot (3x^2+5)
\end{align*}
Klammersetzung nicht vergessen bei $v'(x)$!
Schau dir zur Vertiefung der Kettenregel das passende Lernvideo an!
Regel für die Ableitung von komplizierteren Potenzausdrücken
\begin{align*}
\left((etwas)^p\right)’=p\cdot (etwas)^{p-1} \cdot (etwas)‘
\end{align*}
Das $etwas$ steht für eine beliebige Funktion, wie z.B. $x^3+5x$ oder $e^x$ etc.
Neu!
Produktregel
Die Produktregel wird immer dann angewendet, wenn es sich bei unserer vorhandenen Funktion um ein Produkt handelt. Dazu folgendes Beispiel:
\begin{align*}
&f(x) = 2x\cdot e^x
\end{align*}
Unsere Funktion besteht aus den beiden einzelnen Faktoren $2x$ und $e^x$.
Den ersten Faktor unseres Produkts nennen wir und den zweiten Faktor unseres Produkts nennen wir . Die Produktregel lautet dann ganz allgemein:
\begin{align*}
&f(x)=u(x)\cdot v(x)
\rightarrow f'(x)=u'(x)\cdot v(x) + u(x)\cdot v'(x)
\end{align*}
Also erster Faktor abgeleitet mal zweiter Faktor nicht abgeleitet plus erster Faktor nicht abgeleitet mal zweiter Faktor abgeleitet.
Im nächsten Schritt wollen wir nun die Produktregel auf unser obenstehendes Beispiel anwenden:
\begin{align*}
&f(x)=2x \cdot e^x \quad mit \quad u(x)=2x \quad und \quad v(x)=e^x
\end{align*}
Wir schreiben erstmal die vier benötigten Komponenten auf:
\begin{align*}
&u(x)=2x \\
&u'(x)=2 \\ \\
&v(x)=e^x \\
&v'(x)=e^x \ \textrm{(Die Ableitung von $e^x$ ist immer $e^x$)}
\end{align*}
Jetzt setzen wir diese vier Komponenten nach der obenstehenden Regel wieder zusammen:
\begin{align*}
f'(x)=2\cdot e^x+2x\cdot e^x
\end{align*}
Abschließend fassen wir unseren Term noch zusammen und klammern den gemeinsamen Faktor $e^x$aus:
\begin{align*}
f'(x)=e^x\cdot (2+2x)
\end{align*}
Dieses Vorgehen ist absolut empfehlenswert, da wir jetzt wieder ein Produkt haben und problemlos erneut die Produktregel für die zweite Ableitung anwenden können.
Quotientenregel
Die Quotientenregel wird angewendet, wenn ein Bruch abgeleitet werden soll. Sie hat die allgemeine Form:
\begin{align*}
\left( \frac{u}{v} \right)^{‚} &=\frac{u‘ \cdot v-u \cdot v‘}{v^2}
\end{align*}
Schauen wir uns zum besseren Verständnis folgendes Beispiel mit der Funktion $f(x)= \frac{x^3+2}{x^5}$ an.
Mit $u(x)=x^3+2 \rightarrow u'(x)=3x^2$ und $v(x)=x^5 \rightarrow v'(x)= 5x^4$ lautet die erste Ableitung:
\begin{align*}
f'(x)=\frac{3x^2\cdot x^5-(x^3+2)\cdot 5x^4}{(x^5)^2}= \frac{3x^7-5x^7-10x^4}{x^{10}} = \frac{-2x^7-10x^4}{x^{10}}
\end{align*}
Klammersetzung nicht vergessen bei $u(x)$!
Tipp: Manchmal kann man einen Bruch umformen und benötigt gar nicht die Quotientenregel! Schreibt den Bruch einfach als Produkt und wendet die Produktregel an.
Ableitungsregeln
Um die Ableitung einer Funktion korrekt zu berechnen, muss man einige Ableitungsregeln kennen.
Je nach Aussehen der Funktion kommen dabei eine oder mehrere der nachfolgenden Regeln zum Einsatz:
Ableiten einer Konstanten: $f(x)=C \ \rightarrow f'(x)=0$
Beispiel: $f(x)=5 \rightarrow f'(x)=0 \quad$
Ableiten von x: $f(x)=x \ \rightarrow f'(x)=1 $
Beispiel: $f(x)=x+5 \rightarrow f'(x)=1 \quad$
Potenzregel: $ f(x)=x^p \ \rightarrow f'(x)=px^{p-1}$
Beispiel: $f(x)=x^3 \rightarrow f'(x)=3x^2 \quad$
Faktorregel: $f(x)=c\cdot g(x) \ \rightarrow f'(x)=c\cdot g'(x)$
Beispiel:$f(x)=2 x^3 \rightarrow f'(x)=6x^2 \quad$
Summen-/Differenzregel: $f(x)=g(x) \pm h(x) \rightarrow f'(x)=g'(x)\pm h'(x)$
Beispiel: $ f(x)=x^3 + 2x-5 \rightarrow f'(x)=3x^2+2$.
Neben Potenzfunktionen der Form $f(x)=x^p$ haben wir bereits weitere Funktionen kennengelernt, wie die Exponential- und Logarithmusfunktion.
Bei diesen beiden Funktionen müssen wir uns die Ableitung einfach merken, denn die Ableitung von $f(x)=e^x$ ist z.B. $f'(x)=e^x$. Die Ableitung entspricht also der $e$-Funktion selbst.
Alle wichtigen Ableitungen nochmal im Lernvideo erklärt.
e- und ln-Funktion ableiten
Eine $e$-Funktion wird folgendermaßen abgeleitet: Ihr verwendet „offiziell“ die Kettenregel, aber es geht eigentlich um einiges einfacher. Wir betrachten dafür die Funktion
\begin{align*}
f(x)= e^{5x},
\end{align*}
welche wir nach $x$ ableiten wollen. Dafür schreiben wir einfach den Term mit der $e$-Funktion nochmal hin und multiplizieren das Ding mit dem abgeleiteten Exponenten.
Der Exponent ist hier $5x$ und abgeleitet wäre das einfach $5$. Dann folgt für die Ableitung
\begin{align*}
f'(x)= e^{5x} \cdot 5.
\end{align*}
„Regel“ für die Ableitung von $e$-Funktionen:
\begin{align*}
\left(e^{etwas}\right)’=e^{etwas}\cdot (etwas)‘
\end{align*}
Weitere Beispiele stehen in der Tabelle
\begin{array}{c|c}
f(x) & f'(x)\\ \hline
e^x & e^x\\ \hline
2e^x & 2e^x \\
3e^x & 3e^x \\ \hline
e^{2x} & 2e^{2x} \\
e^{3x} & 3e^{3x} \\
e^{x^2} & 2xe^{x^2} \\
e^{2-4x} & -4e^{2-4x} \\ \hline
20e^{3x} & 3 \cdot 20 e^{3x} \\
x \cdot e^{2x} & Produktregel
\end{array}
Falls eine $e$-Funktion mit anderen Funktionen multipliziert wird, müssen wir die bereits bekannte Produktregel anwenden.
Beispiel e-Funktion ableiten:
\begin{align*}
f(x)&= \underbrace{(x^2-2)}_{u(x)} \cdot \underbrace{e^{-2x}}_{v(x)} \\
\textrm{mit} \quad u(x)&=x^2-2 \quad u'(x)=2x \\
\textrm{und} \quad v(x)&=e^{-2x} \quad \quad v'(x)= -2e^{-2x}
\end{align*}
Somit ergibt sich für die erste Ableitung:
\begin{align*}
f'(x)=2xe^{-2x}+(x^2-2) \cdot (-2e^{-2x})
\end{align*}
Oft ist es hilfreich, die Anteile mit $e$ auszuklammern. Gerade wenn dieser Ausdruck gleich 0 gesetzt wird, z.B. um die Extremstellen zu bestimmen. Vereinfacht folgt:
\begin{align*}
f'(x) &= e^{-2x} (2x+(x^2-2)(-2)) \\
&=e^{-2x}(2x-2x^2+4) \\
&=e^{-2x}(-2x^2+2x+4)
\end{align*}
Wird von uns die Ableitung der $\ln$-Funktion verlangt, müssen wir zunächst wissen, dass die Ableitung von $f(x)=\ln(x) \rightarrow f'(x)=1/x$ ist. Steht statt dem $x$ etwas anderes da, muss die Kettenregel verwenden.
„Regel“ für die Ableitung von $\ln$-Funktionen:
\begin{align*}
\left(\ln(etwas)\right)’=\frac{1}{etwas} \cdot (etwas)‘
\end{align*}
Beispiel Ableiten ln-Funktion
\begin{align*}
f(x)=\ln(5x^2-3x) \rightarrow f'(x)&=\frac{1}{5x^2-3x} \cdot (5x^2-3x)‘ \\ &=\frac{1}{5x^2-3x} \cdot (10x-3)
\end{align*}
Mit den eingeführten „Regeln“ können wir $e$– und $\ln$-Funktionen leicht ableiten.
Neu!

