
Determinante
Die Determinante (Mathematisch auch die Determinantenfunktion genannt) ordnet jeder quadratischen Matrix ${A}\in\mathbb{R}^{n\times n}$ eine Zahl $a\in\mathbb{R}$ zu:
\begin{align*}
&{f}:\mathbb{R}^{n{ x }n}\rightarrow\mathbb{R},\textbf{A}\rightarrow \text{det}(\textbf{A}) \\
\text{oder}\quad&{f}: \mathbb{R}^{n{ x }n}\rightarrow\mathbb{R},\textbf{A}\rightarrow{|\textbf{A}|}
\end{align*}
Inhalt auf dieser Seite
- Was gibt die Determinante an?
- Rechenregeln zu Determinanten
- Berechnung von Determinanten
- Anwendung von Determinanten
Was gibt die Determinante an?
Die Determinante einer Matrix ${A}$ ($\det({A})$ oder $|{A}|$) gibt an, wie sich das Volumen einer aus Eckpunkten zusammengesetzten Geometrie skaliert, wenn diese durch die Matrix $A$ abgebildet wird. Ist die Determinante negativ, so ändert sich zusätzlich die Orientierung der Eckpunkte.
- Das bedeutet, dass die Eckpunkte einer Geometrie in einen Untervektorraum abgebildet werden, der von niedrigerer Dimension ist als der, aus dem die Spaltenvektoren der Matrix stammen, z.B. wenn eine 3$x$3-Matrix Punkte aus dem Raum ($\dim(\mathbb{R}^3)$=3) auf eine zweidimensionale Ebene (oder auf eine 1-dimensionale Gerade) abbildet.
- Das bedeutet dann, dass die Spaltenvektoren der Matrix keine Basis bilden.
- Daraus lässt sich wiederum schließen, dass die Spaltenvektoren linear abhängig sind.
- Also ist die Matrix nicht invertierbar $\ldots$ usw.
\begin{align}
\text{det}(A) \begin{cases} \neq 0 & \Rightarrow \ {A}^{-1}\text{ existiert.} \\
=0 & \Rightarrow \ {A}^{-1} \text{ existiert nicht.}\end{cases}
\end{align}
Hier nochmal ein Grundlagenvideo zur Determinante
Rechenregeln zu Determinanten
Matrix A ist quadratisch ($\textbf{A}\in\mathbb{R}^{n x n}$). Daher gelten die folgenden Rechengesetze:
\begin{align*}
& \text{det}(\textbf{A}\cdot \textbf{B})&&=\text{det}(\textbf{A})\cdot \text{det}(\textbf{B})\\[2mm]
& \text{det}(\textbf{A}^T)&&=\text{det}(\textbf{A})\\[2mm]
& \text{det}(\textbf{A}^{-1})&&=\frac{1}{\text{det}(\textbf{A})}\\[2mm]
& \text{det}(m\cdot\textbf{A})&&=m^n\cdot\text{det}(\textbf{A})\quad\text{mit}\quad m\in\mathbb{R}
\end{align*}
Wenn $\text{det}(\textbf{A})=a$ ist, dann gilt:
- Multiplikation einer Zeile (Spalte) von A mit einer Zahl $\lambda$ $\Rightarrow \text{det}(\textbf{A})=\lambda\cdot a$
- Vertauschen von 2 Zeilen (2 Spalten) von A $\Rightarrow \det(\widetilde{\textbf{A}})=-a$
- Addition eines Vielfachen einer Zeile zu einer anderen Zeile $\Rightarrow \det(\widetilde{\textbf{A}})=a$
- Addition eines Vielfachen einer Spalte zu einer anderen Zeile $\Rightarrow \det(\widetilde{\textbf{A}})=a$
„…zu einer anderen Zeile (Spalte)“‚. Diese Zeile (Spalte) müssen wir bei der veränderten Matrix verändern und nicht die Zeile (Spalte), von der wir ein Vielfaches für die Rechnung genommen haben!
..mit $\widetilde{\textbf{A}}$ als Matrix $\textbf{A}$ nach der jeweiligen Manipulation
Beispiel
Zu 1) Erste Zeile mit 3 multipliziert
\begin{align*}
\text{det}(\textbf{A})=\text{det}
\left(
\begin{matrix} % 3×3
3 & -1 & 2 \\
0 & 3 & 4 \\
1 & -2 & 0
\end{matrix}\right)=-14,\qquad\text{det}(\widetilde{\textbf{A}})=\text{det}
\left(
\begin{matrix} % 3×3
9 & -3 & 6 \\
0 & 3 & 4 \\
1 & -2 & 0
\end{matrix}\right)=3\cdot -14=-42
\end{align*}
Zu 2) Zweite und dritte Spalte getauscht.
\begin{align*}
\text{det}(\textbf{A})=\text{det}
\left(
\begin{matrix} % 3×3
3 & -1 & 2 \\
0 & 3 & 4 \\
1 & -2 & 0
\end{matrix}
\right)=-14,\qquad\text{det}(\widetilde{\textbf{A}})=\text{det}
\left(
\begin{matrix} % 3×3
3 & 2 & -1 \\
0 & 4 & 3 \\
1 & 0 & -2
\end{matrix}
\right)=14
\end{align*}
Zu 3) $3\cdot\text{„dritte Zeile“}-\text{„erste Zeile“}\Rightarrow$ wird neue erste Zeile
\begin{align*}
\text{det}(\textbf{A})=\text{det}
\left(
\begin{matrix} % 3×3
3 & -1 & 2 \\
0 & 3 & 4 \\
1 & -2 & 0
\end{matrix}
\right)=-14,\qquad\text{det}(\widetilde{\textbf{A}})=\text{det}
\left(
\begin{matrix} % 3×3
0 & -5 & -2 \\
0 & 3 & 4 \\
1 & -2 & 0
\end{matrix}
\right)=-14
\end{align*}
Berechnung von Determinanten
Das allgemeine Verfahren zum Berechnen von Determinanten einer $n$ x $n$-Matrix ist der Laplace’sche Entwicklungssatz. Speziell für eine 3 x 3-Matrix gibt es die Regel von Sarrus und das Rechenschema für eine 2 x 2-Matrix solltest du dir auch abseits des Entwicklungssatzes merken.
1 x 1 Matrix
Determinante einer 1 x 1 Matrix entspricht ihrem einzigen Element.
2 x 2 Matrix
\begin{align}
&\text{det}
\left(
\begin{matrix}
a & b \\
c & d
\end{matrix}\right)=a \cdot d \ – \ c \cdot b
\end{align}
3 x 3 Matrix – Regel von Sarrus
\begin{align}
&\text{det}
\left(
\begin{matrix}
a & b & c \\
d & e & f \\
g & h & i \\
\end{matrix}\right) = aei+bfg+cdh-ceg-bdi-afh
\end{align}
n x n Matrix – Laplace’scher Entwicklungssatz (allgemeines Verfahren)
\begin{align}%
\text{Entweder}\quad\text{det}(\textbf{A})&=\sum_{j=1}^n\left[a_{ij}\cdot(-1)^{i+j}\cdot D_{ij}\right]\quad \text{Entwicklung nach $i$-ter Zeile}\\
\text{oder}\quad\text{det}(\textbf{A})&=\sum_{i=1}^n\left[a_{ij}\cdot(-1)^{i+j}\cdot D_{ij}\right]\quad \text{Entwicklung nach $j$-ter Spalte}
\end{align}
Was bedeuten die Formeln bzw. wie sind diese zu lesen?
- Es ist völlig egal, nach welcher Zeile oder Spalte entwickelt wird (möglichst nach der Zeile/Spalte mit den meisten Nullen)
- Term $a_{ij}$: Das Element $a_{ij}$ aus der Matrix A
- Term $(-1)^{i+j}$: „Schachbrettregel für Vorzeichen“.
Merke dir die Matrix mit dem Vorzeichenschema
\begin{align*}
\left(
\begin{matrix}
+ & – & + & – & \cdots \\
– & + & – & + & \cdots \\
+ & – & + & – & \cdots \\
– & + & – & + & \cdots \\
\vdots & \vdots & \vdots & \vdots & \ddots
\end{matrix}
\right)
\end{align*} - Term $D_{ij}$: Die sogenannte Unterdeterminante (oder der Minor) der Matrix A, wenn die $i$-te Zeile und $j$-te Spalte von A heraus gestrichen wird
\begin{align*}
\textbf{A}=
\left(
\begin{matrix} % 3×3
1 & 3 & 8 \\
-2 & 5 & 0 \\
4 & 6 & 7
\end{matrix}\right),\quad D_{32}=
\left|
\begin{matrix} % 2×2
1 & 8 \\
-2 & 0
\end{matrix}\right|,\quad D_{13}=
\left|
\begin{matrix} % 2×2
-2 & 5 \\
4 & 6
\end{matrix}\right|,\quad D_{22}=
\left|
\begin{matrix} % 2×2
1 & 8 \\
4 & 7
\end{matrix}
\right|
\end{align*} - (Terme $(-1)^{i+j}\cdot D_{ij}$ nennen sich Kofaktoren der Matrix A.)
Weiteres Beispiel
\left(\begin{matrix} % 4×4
-4 & 0 & \pmb{-1} & -1 \\
2 & 2 & \pmb{0} & 2 \\
-2 & 3 & \pmb{1} & -5 \\
-1 & 1 & \pmb{0} & -2
\end{matrix}\right)
$
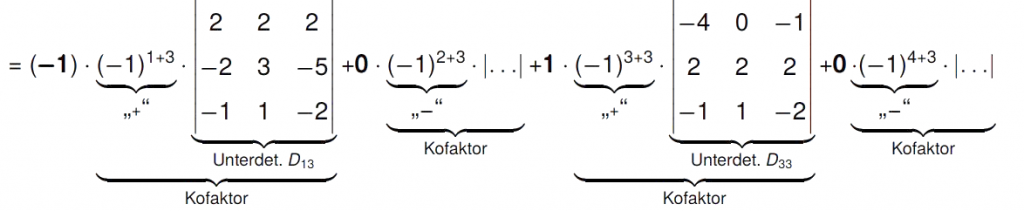
\stackrel{\phantom{Sarrus}}{=}-(2)+(20)=18$
Anwendung von Determinanten
Wozu sollten wir Determinanten berechnen?
Es ist ein „mathematisches Werkzeug“, mit dem wir einfach überprüfen können, ob:
- Eine (quadratische) Matrix invertierbar/regulär ist
- Eine Abbildung ein Automorphismus (und damit auch Iso-, Mono- und Epimorphismus) ist
- Ein gegebenes EZS eine Basis ist
- … usw …
Beispiel
Für welche Parameter $a\in\mathbb{R}$ ist die Abbildung $f_A$ ein Isomorphismus?
\begin{align*}
f_A:{\mathbb{R}^3}\rightarrow\mathbb{R}^3,\overrightarrow{x}\rightarrow\textbf{A}\overrightarrow{x}\quad\text{mit}\quad\textbf{A}=
\left(
\begin{matrix} % 3×3
-1 & 2 & 9+a \\
1+a & 4-a & -3 \\
a & 2 & 4
\end{matrix}
\right)
\end{align*}
Kluges Vorgehen: Wenn $f_A$ ein Isomorphismus ist, ist es auch ein Automorphismus ($f_A$ ist schon ein Endomorphismus, da von $\mathbb{R}^3$ nach $\mathbb{R}^3$ abgebildet wird). Wenn dem so ist, existiert ${A}^{-1}$ und damit muss det(A)=0 sein.
det(A) berechnen: In Matrix A ist kein Eintrag 0. Wir können aber z.B. Zeile $3\cdot(-1)$ nehmen und auf die erste Zeile addieren. So ändert sich die Determinante nicht, Element $a_{12}$ wird Null und wir haben Rechenschritte gespart (Kein Muss!). Danach Entwicklung nach 2. Spalte:
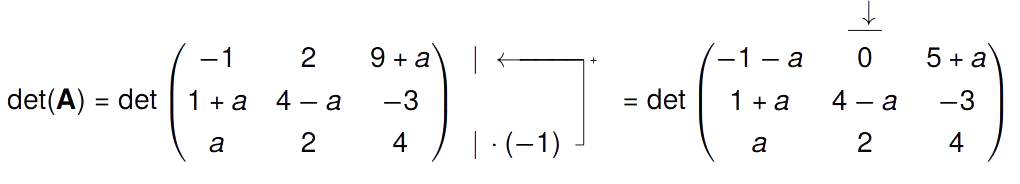
\begin{align*}
&=+(4-a)\Bigl((-1-a)\cdot 4-a(5+a)\Bigr)-2\Bigl((-1-a)(-3)-(1+a)(5+a)\Bigr)\\
&=(4-a)\Bigl(-4-4a-5a-a^2\Bigr)-2\Bigl(3+3a-5-6a-a^2\Bigr)\\
&=(4-a)\Bigl(-a^2-9a-4\Bigr)-2\Bigl(-a^2-3a-2\Bigr)=(a-4)\Bigl(a^2+9a+4\Bigr)+2\Bigl(a^2+3a+2\Bigr)\\
&=a^3+9a^2+4a-4a^2-36a-16+2a^2+6a+4\\
&=a^3+7a^2-26a-12
\end{align*}
Nun det(A)=0 setzen, um die $a$ zu berechnen, die nachher ausgeschlossen werden müssen!
det(A) ist ein Polynom dritten Grades. Wenn eine „schöne“ Lösung für $a$ existiert ($a\in\mathbb{Z}$), dann ist diese Teiler vom Absolutglied (-12). Also $a\in\left\{-12,-6,-4,-3,-2,-1,1,2,3,4,6,12\right\}$. Durch ausprobieren (Empfehlung: Funktionswert durch Horner-Schema ausrechnen) finden wir $a=3$ als eine Lösung. Polynom durch Horner-Schema auftrennen:
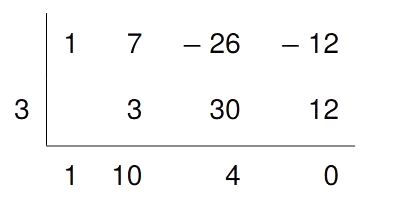
$\Rightarrow a^3+7a^2-26a-12=\underbrace{(a-3)}_{a_1\,=\,3}\underbrace{(a^2+10a+4)}_{a\,=\,?}=0\stackrel{pq}{\quad} a_{2,3}=-5\pm\sqrt{21}$
Also ist $f_A$ ein Isomorphismus, wenn $a\in\mathbb{R}\setminus\left\{3,-5-\sqrt{21},-5+\sqrt{21}\right\}$