
Einaxial belastete Stäbe
Bei diesen Aufgabentypen ist in der Regel nach Längenänderungen oder Spannungen gefragt. Allgemein gilt: Spannung = Kraft pro Fläche!
Lösungsschritte (vgl. Rolf Mahnken, Lehrbuch der Technischen Mechanik – Elastostatik, Springer Verlag, 1. Auflage, 2015)

19,99€
(i) für statisch bestimmte Stäbe
- Statisches System: Idealisierung in $n$ Stäbe. Zusätzliche Balken werden als starr angenommen.
- Gleichgewichtsbedingungen aufstellen
- Spannungen: Für jeden Stab gilt
\begin{align*}
\sigma_i = \frac{N_i}{A_i} \quad \textrm{mit} \quad i=1, \ \dots \ , \ n
\end{align*}
- Längenänderungen:
\begin{align*}
\Delta l_i = \frac{N_i \cdot l_i}{(EA)_i} + \alpha_{T_i} \cdot \Delta T_i \cdot l_i
\end{align*}
- Verschiebung von Stabendpunkten
$\rightarrow$ Grafo-analytisch zur Berücksichtigung der Kompatibilität
- Weitere Aufgabenstellungen: Spannungs- und Verformungsnachweis, Dimensionierung etc.
z.B. 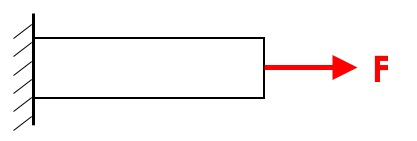
$\rightarrow$ statisch bestimmt, da Auflagerreaktionen über Gleichgewichtsbedingungen ermittelbar sind!
(ii) für statisch unbestimmte Stäbe
- Statisches System
- Gleichgewichtsbedingungen
- Grad der statischen Unbestimmtheit $n_s$
- Vergleich von Anzahl an Unbekannten mit Gleichgewichtsbedingungen
- Kompatibilitätsbedingungen
\begin{align*}
\Delta l_i = \frac{N_i \cdot l_i}{(EA)_i} + \alpha_{T_i} \cdot \Delta T_i \cdot l_i
\end{align*}
und $n_s$ Kompatibilitätsbedingungen mit Hilfe eines Pol- und Verschiebungsplanes, z.B. $\Delta l_i = 2 \Delta l_k$
- Auflösen des Gleichungssystems
- Weitere Aufgabenstellungen: Spannung, Längenänderung, Verdrehung etc.
z.B. 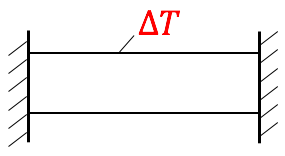
$\rightarrow$ statisch bestimmt, da Auflagerreaktionen über Gleichgewichtsbedingungen ermittelbar sind!
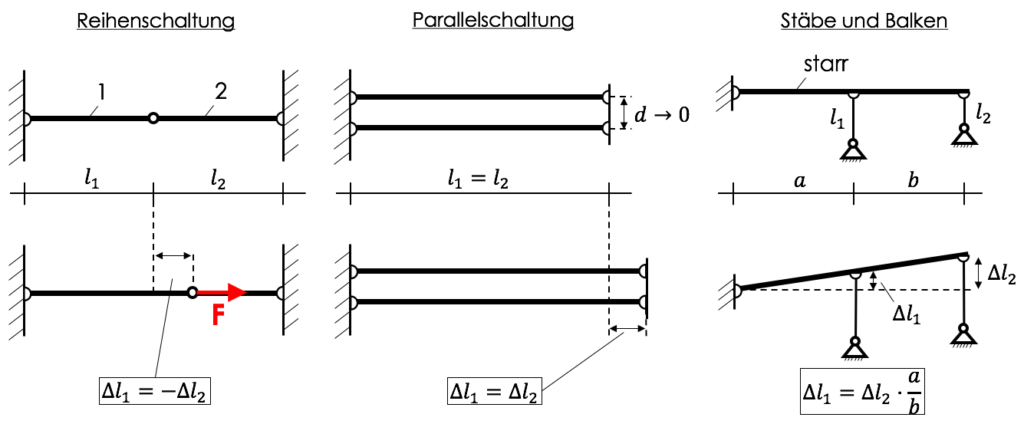
Kompatibilitätsbedingungen für statisch unbestimmte Stäbe
Aufgabe zu einaxial belasteten Stäben
Gegeben ist nebenstehendes System.
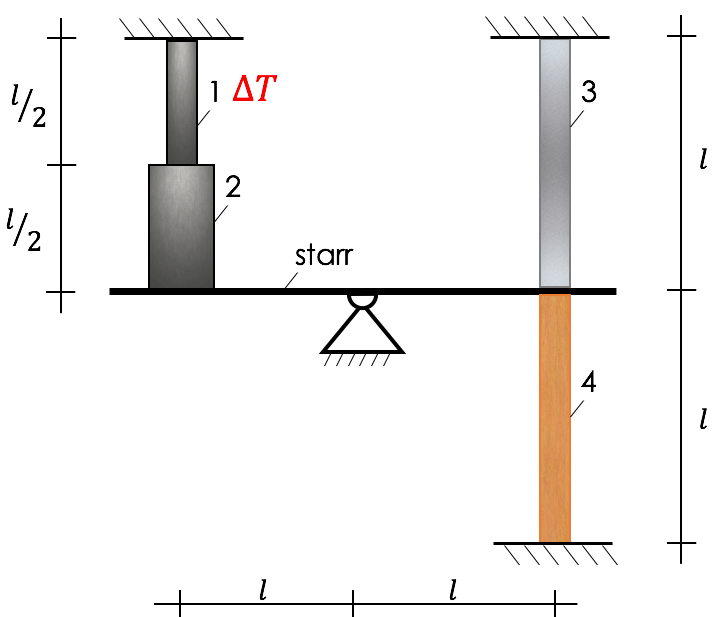
Folgende Aufgaben sind zu erfüllen:
- Erstelle ein statisches Ersatzsystem.
- Berechne alle Stabkräfte.
- Ermittle die Spannungen in allen Stäben.
Bekannt: $A_1 = A_3 = A_4 = 30 \ \textrm{cm}^2, \ A_2 = 2 A_1, \ E_{1,2} = 210 \ \textrm{GPa},$ $E_3 = 70 \ \textrm{GPa}, \ E_4 = 100 \ \textrm{GPa}$, $l=1 \ \textrm{m}, \ \Delta T = 50 \ \textrm{K}$
Video ähnliches Beispiel einaxial belastete Stäbe mit thermischem Anteil
