Der Mohr’sche Spannungskreis
Wenn es um den Mohr’schen Spannungskreis geht, werden in der Regel folgende Aufgabentypen behandelt:
(i) Ermittlung von Hauptspannungen
(ii) Ermittlung der Spannungen in gedrehten Koordinatensystemen
Gegeben sei der ebene Spannungszustand $\underline{\underline{\sigma}} = \begin{pmatrix} \sigma_x & \tau_{xy} \\ \tau_{yx} & \sigma_y \end{pmatrix}$. Zu den typischen Aufgabentypen schauen wir uns folgende Lösungsschritte an (vgl. Rolf Mahnken, Lehrbuch der Technischen Mechanik – Elastostatik, Springer Verlag, 1. Auflage, 2015).
Lösungsschritte zu (i):
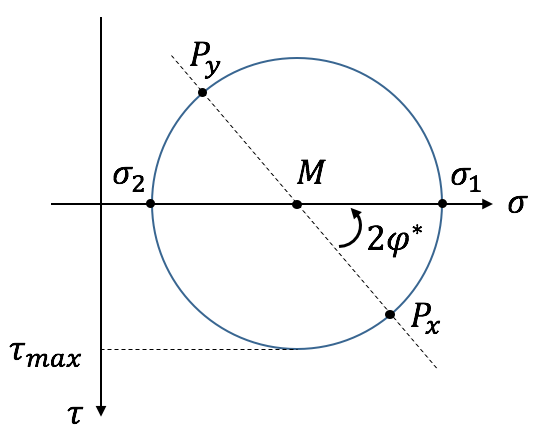
- Achsen $\sigma-\tau$ zeichnen – $\tau$ positiv nach unten!
- Eintragen der Punkte: $P_x = ( \sigma_x; \ \tau_{xy} )$ und $P_y = ( \sigma_y; \ -\tau_{xy} )$
-
Schnittpunkt der Verbindungslinie $\overline{P_xP_y}$ mit $\sigma$-Achse liefert Kreismittelpunkt $M$
- Kreis um $M$ mit Radius $\overline{MP_x}$ zeichnen
- Hauptspannungen $\sigma_1, \ \sigma_2$ aus Schnittpunkt mit $\sigma$-Achse abgreifen
- Doppelten Hauptspannungswinkel ablesen $2\varphi^*$
Lösungsschritte zu (ii):
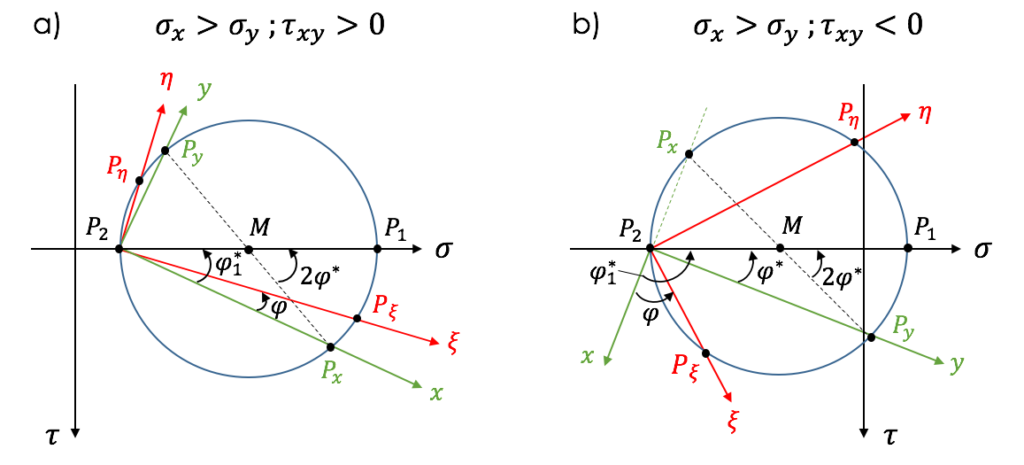
- Verbindungen von $P_2$ mit $P_x$ und $P_y$ legen $x-y$-Achsen fest! Richtungssinn von $x$ beliebig, unter Beachtung eines Rechtssystems folgt der Richtungssinn von $y$.
- Von $x$-Achse ausgehend für gegebenen Winkel $\varphi$ die $\xi$-Achse (\xi = Xi) zeichnen
- Unter Beachtung des Richtungssinnes folgt die $\eta$-Achse ($\eta$= Eta)
$\rightarrow$ Merke: Aus $x$ wird Xi und aus $y$ wird Eta! - Schnittpunkte der $\xi-\eta$-Achse mit Kreis legen Punkte $P_\xi$ und $P_\eta$ fest
- Abgreifen der Spannungen $P_\xi=(\sigma_\xi , \ \tau_{\xi\eta})$ und $P_\eta=(\sigma_\eta , \ -\tau_{\xi\eta})$
Rechnerische Bestimmung:
(i) Hauptnormalspannungen (kurz: Hauptspannungen)
\begin{align*}
1. \ \sigma_1 &= \sigma_{max} = \frac{\sigma_x + \sigma_y}{2} + \sqrt{ \left( \frac{\sigma_x – \sigma_y}{2} \right)^2 + \tau_{xy}^2} \\
2. \ \sigma_2 &= \sigma_{max} = \frac{\sigma_x + \sigma_y}{2} – \sqrt{ \left( \frac{\sigma_x – \sigma_y}{2} \right)^2 + \tau_{xy}^2} \\
3. \ \tau_{12} &= 0
\end{align*}
$\rightarrow$ In Hauptspannungsrichtung verschwindet Schubspannung!
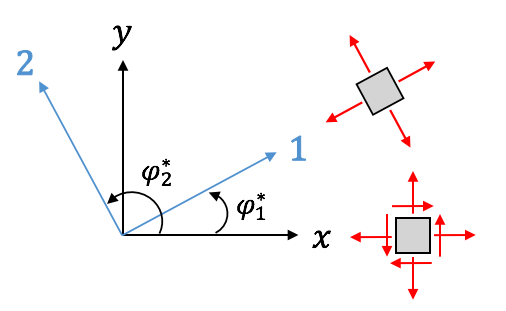
- Winkel der maximalen/minimalen Hauptspannungsrichtung:
\begin{align*}
\tan \varphi_1^* = \frac{\tau_{xy}}{\sigma_1 – \sigma_y} \quad \textrm{und} \quad \varphi_2^*=\varphi_1^*+\frac{\pi}{2}
\end{align*}
- Kontrolle über Invarianten:
\begin{align*}
1. \ J_{1\sigma} = \sigma_x + \sigma_y = \sigma_1 + \sigma_2 \\
2. \ J_{2\sigma} = \sigma_x \cdot \sigma_y -\tau_{xy}^2 = \sigma_1 \cdot \sigma_2
\end{align*}
(ii) Hauptschubspannungen
\begin{align*}
&1. \ \sigma_{\xi} ( \tilde{\varphi} ) = \sigma_{\eta} ( \tilde{\varphi} ) = \frac{\sigma_x + \sigma_y}{2} = \frac{\sigma_1 + \sigma_2}{2} = \sigma_M \\
&2. \ \tau_{max/min} = \pm \sqrt{ \left( \frac{\sigma_x-\sigma_y}{2} \right)^2 + \tau_{xy}} = \pm \frac{\sigma_1-\sigma_2}{2} = \pm \sigma_R
\end{align*}
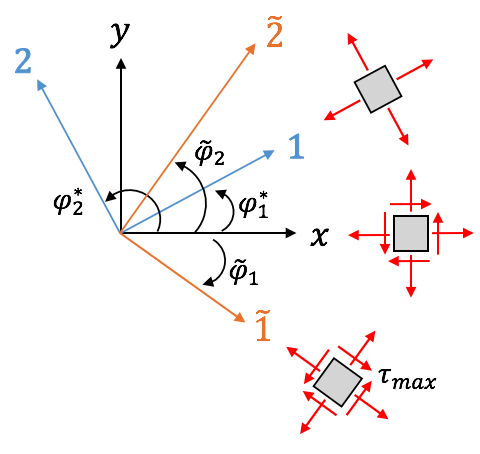
mit den Winkeln der Hauptschubspannungsachsen:
\begin{align*}
\tilde{\varphi}_1 = \varphi_1^*-\frac{\pi}{4} \quad \textrm{und} \quad \tilde{\varphi}_2 = \varphi_1^*+\frac{\pi}{4}
\end{align*}
Video typische Belastungsfälle beim Mohrschen Spannungskreis
Aufgabe zum Mohr’schen Spannungskreis
Gegeben ist der folgende ebene Spannungszustand $\underline{\underline{\sigma}} = \begin{pmatrix} 10& -40 \\ -40 & -80 \end{pmatrix}$.
Bestimme zeichnerisch/rechnerisch
- die Hauptspannungen,
- die maximale Schubspannung,
- den Hauptspannungswinkel,
- die Spannungen für ein um 45° gedrehtes Koordinatensystem.
Welche Vergleichsspannungshypothesen gibt es und in welchen Bereichen finden die jeweiligen Hypothesen Anwendung?
Video Mohrscher Spannungskreis ähnliches Beispiel

19,99€