
Lineare Gleichungssysteme
Wir werden uns in diesem Artikel mit dem Thema Lineare Gleichungssysteme (auch LGS genannt) beschäftigen.
- Was sind lineare Gleichungssysteme?
- Von einer linearen Gleichung zum Gleichungssyslinetem
- LGS lösen mit Einsetzungsverfahren
- LGS lösen mit Gleichsetzungsverfahren
- Sonderfälle
- LGS lösen mit Additionsverfahren
- Gauß-Algorithmus
Weißt du noch was eine lineare Gleichung ist? Dabei handelt es sich um eine Gleichung ersten Grades, d.h. die Variable $x$ kommt in keiner höheren als der ersten Potenz vor. Die Parameter $a$ und $b$ können reelle Zahlen annehmen, wobei $a\neq 0$ gilt.
Allgemeine Form: $ax+b=0$
Neu!
Was sind lineare Gleichungssysteme (LGS)?
Bei linearen Gleichungssystemen befinden sich die Graphen von zwei linearen Funktionen (also Geraden) innerhalb eines Koordinatensystems. In diesem Zusammenhang stellen wir fest, dass zwei Geraden zueinander entweder:
- parallel oder
- identisch sind bzw.
- einen gemeinsamen Schnittpunkt
Es geht also darum, herauszufinden, welcher dieser drei Fälle vorliegt. Das kann auf zwei verschiedene Arten geschehen:
- zeichnerisch oder
- rechnerisch
In diesem Zusammenhang betrachten wir die zwei folgenden Funktionen:
- $y=-x+2$
- $y=2x-1$
Die Darstellung im Koordinatensystem sieht aus wie folgt:
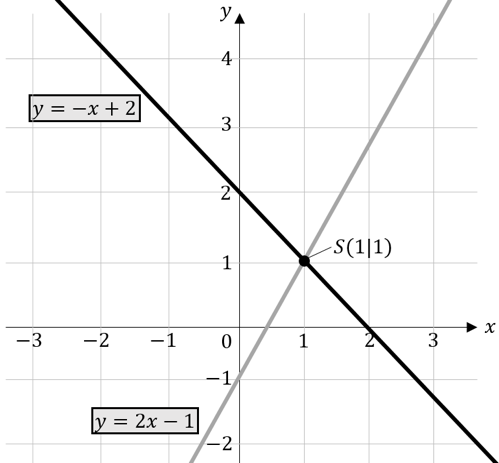
Wir können hier sehr gut erkennen, dass die beiden Geraden sich im Punkt $(1|1)$ schneiden. Des Weiteren fällt uns auf, dass unsere beiden Geraden unterschiedliche Steigungen haben, nämlich $-1$ und $2$.
In diesem Zusammenhang halten wir also fest, dass Geraden mit unterschiedlicher Steigung immer einen gemeinsamen Schnittpunkt haben. Im Umkehrschluss bedeutet das, dass Geraden mit identischer Steigung parallel zueinander verlaufen oder sogar identisch sind. Identisch sind sie aber nur dann, wenn sie ebenfalls den gleichen Schnittpunkt mit der $y$-Achse haben. Wir halten also fest:
- $m_1\neq m_2$ $\Longrightarrow $ gemeinsamer Schnittpunkt
- $m_1=m_2\wedge b_1\neq b_2$ $\Longrightarrow $ parallel
- $m_1=m_2\wedge b_1=b_2$ $\Longrightarrow $ identisch
[$m_1=$ Steigung der ersten Geraden; $m_2=$ Steigung der zweiten Geraden; $b_1=$ Schnittpunkt mit der $y$-Achse der ersten Geraden; $b_2=$ Schnittpunkt mit der $y$-Achse der zweiten Geraden]
Von einer linearen Gleichung zum Gleichungssystem
Als lineares Gleichungssystem bezeichnet man ein System linearer Gleichungen, die mehrere Unbekannte („Variablen“) enthalten.
Schauen wir uns dazu ein kleines Beispiel an
\begin{align*}
3x_1+4x_2&=-1 \\
2x_1+5x_2&=3
\end{align*}
Der Unterschied zwischen einer linearen Gleichung und einem linearen Gleichungssystem ist das Vorhandensein
- mehrerer Gleichungen
- mehrerer Unbekannten
Im Zusammenhang mit Linearen Gleichungs-Systemen wird auch oft die Abkürzung „LGS“ verwendet.
Allgemeine Form:
\begin{align*}
a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n &= b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n &= b_2 \\ \vdots \quad \quad \vdots \quad \quad \qquad & \vdots \\ a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n &= b_m
\end{align*}
Beispiel:
\begin{align*} 3x_1 – 2x_2 + 2x_3 &= 1 \\ -2x_1 + 5x_2 – 6x_3 &= 0 \\ 4x_1 + 3x_2 – 2x_3 &= 3 \end{align*}
Gleichungssysteme mit $m$ Gleichungen und $n$ Unbekannten kann man folgendermaßen kategorisieren
- Quadratisches Gleichungssystem $m=n$, z.B. 3 Gleichungen und 3 Unbekannte
- Unterbestimmtes Gleichungssystem $m<n$, z.B. 2 Gleichungen und 3 Unbekannte
- Überbestimmtes Gleichungssystem $m>n$, z.B. 3 Gleichungen und 2 Unbekannte
Bei dem Thema lineare Gleichungssysteme geht es hauptsächlich darum, diese zu lösen. Dazu bedient man sich sog. Lösungsverfahren, die dir bei der Ermittlung der Lösung helfen sollen. In der Schule beschäftigt man sich in der Regel mit folgenden Verfahren:
- Additionsverfahren
- Einsetzungsverfahren
- Gleichsetzungsverfahren
Jedes Verfahren kann man zum lösen von Gleichungssystemen nutzen. Jedoch ist das Additionsverfahren das Wichtigste, da für lineare Gleichungssysteme mit drei oder mehr Variablen systematische Lösungsverfahren genutzt werden sollten. Hier ist insbesondere das Gauss-Verfahren zu nennen, das auf einem Additionsverfahren beruht.
Es werden 3 Fälle für die Lösungen von Gleichungssystemen unterschieden:
- eine eindeutige Lösung, wenn z.B. als Lösung $x_1=5, x_2=4$ herauskommt.
- keine Lösung, wenn z.B. als Lösung $3=4$ eine falsche Aussage herauskommt.
- unendlich viele Lösungen, wenn z.B. als Lösung $0=0$ eine allgemeingültige Aussage herauskommt.
NEU
LGS lösen mit Einsetzungsverfahren
So gehst du beim Einsetzungsverfahren vor:
- Auflösen einer Gleichung nach einer Variablen.
- Einsetzen des für diese Variable berechneten Terms in die andere Gleichung.
- Auflösen der so entstandenen Gleichung nach der enthaltenen Variablen.
- Einsetzen der Lösung in die Gleichung, die im 1. Schritt berechnet wurde, mit anschließender Berechnung der Variablen.
Beispiel für ein quadratisches Gleichungssystem mit 2 Gleichungen und 2 Unbekannten:
\begin{align*}
\text{I} \ \ 2x_1 + 3x_2 &= 12 \\
\text{II} \quad \ \ x_1 – x_2 &= 1
\end{align*}
Gleichung $\text{II}$ nach $x_1$ umformen:
\begin{align*}
x_1=x_2+1
\end{align*}
nun $x_1$ in Gleichung $\text{I}$ einsetzen und nach der enthaltenden Unbekannten auflösen
\begin{align*}
2(x_2+1)+3x_2&=12 \quad |\ \textrm{zusammenfassen} \\
5x_2+2 &= 12 \quad |-2 \\
5x_2&=10 \quad |:5 \\
x_2&=2
\end{align*}
Die Lösung $x_2 =2$ in die umgeformte Gleichung $x_1=x_2+1$ aus dem ersten Schritt einsetzen und so die andere Variable berechnen. Es folgt $x_1=x_2+1=2+1=3$.
Schau dir zur Vertiefung Daniels Lernvideos zum Thema LGS lösen mit „Einsetzungsverfahren“ an.
LGS lösen mit Gleichsetzungsverfahren
Vorgehen:
- Auflösen beider Gleichungen nach der gleichen Variablen.
- Gleichsetzen der anderen Seiten der Gleichung.
- Auflösen der so entstandenen Gleichung nach der enthaltenen Variablen.
- Einsetzen der Lösung in eine der umgeformten Gleichung aus Schritt 1 mit anschließender Berechnung der Variablen.
Beispiel für ein quadratisches Gleichungssystem mit 2 Gleichungen und 2 Unbekannten:
\begin{align*}
\text{I} \ \ 2x_1 + 3x_2 = 12 \\
\text{II} \quad \ \ \ x_1 – x_2 = 1
\end{align*}
Beide Gleichungen nach der selben Variable umformen, z.B. $x_1$.
\begin{align*}
\text{Ia} \ \ x_1 &= 6 – 1,5x_2 \\
\text{IIa} \ \ x_1 &=x_2 + 1
\end{align*}
Nun Gleichung $\text{Ia}$ und $\text{IIa}$ gleichsetzen, denn es gilt $x_1=x_1$. Es folgt
\begin{align*}
6 – 1,5x_2 = x_2 + 1
\end{align*}
Entstandene Geichung nach $x_2$ auflösen:
\begin{align*}
6 – 1,5x_2 &= x_2 + 1 \quad |+1,5x_2 \ -1 \\
5 &= 2,5x_2 \quad \ |:2,5 \\
2 &=x_2
\end{align*}
Abschließend noch die Lösung in eine der umgeformten Gleichungen aus dem ersten Schritt (also in $\text{Ia}$ oder $\text{IIa}$) einsetzen und die andere Variable berechnen. Wir setzen $x_2=2$ in $\text{IIa}$ ein und erhalten: $x_1=2+1=3$.
Daniel zeigt euch nochmal wie man mit dem Gleichsetzungsverfahren LGS lösen kann.
Sonderfälle
Wie am Anfang schon kurz beschrieben, ist es möglich, dass sich unsere beiden Geraden nicht schneiden, sondern parallel oder sogar identisch sind. Wenn dieser Fall eintritt, bekommen wir natürlich bei unserer Berechnung auch keine Schnittpunktkoordinaten. Wir gucken uns jetzt zu beiden Fällen jeweils eine Aufgabe an, damit ihr nicht verwirrt seid, falls so ein Fall in der Prüfung auftauchen sollte.
Parallele Geraden
Zwei parallele Geraden haben die gleiche Steigung, aber nicht den gleichen Schnittpunkt mit der $y$-Achse. Dazu betrachten wir das folgende lineare Gleichungssystem:
\begin{align*}
\begin{array}{rrcl}
\textrm{I} & y &=&2x-2 \\
\textrm{II} & y &=& 2x-5
\end{array}
\end{align*}
Wir sehen auf den ersten Blick, dass unsere beiden Steigungen identisch sind. Das gilt hier aber nicht für die Schnittpunkte mit der $y$-Achse.
Wir wenden jetzt das Gleichsetzungsverfahren an und gucken was passiert:
\begin{align*}
2x-2&=2x-5 | -2x \\ \\
-2&=-5
\end{align*}
Wir erhalten eine falsche Aussage, denn $-2$ ist eben nicht gleich $-5$. Damit hätten wir gezeigt, dass es keine Lösung gibt, also dass sich die Geraden nicht schneiden und dass unsere Geraden daher parallel zueinander verlaufen.
Identische Geraden
Zwei identische Geraden lassen sich nicht immer gleich auf den ersten Blick erkennen. Dazu das folgende Beispiel:
\begin{align*}
\begin{array}{rrcl}
\textrm{I} & 4x &=&5-y \\
\textrm{II} & 8x &=& 10-2y
\end{array}
\end{align*}
Im ersten Moment sieht es nicht so aus, als wären diese beiden Geraden identisch, denn sowohl die Steigungen als auch die Schnittpunkte mit der $y$-Achse scheinen unterschiedliche Werte zu haben. Doch nehmen wir an, dass wir jetzt das Gleichsetzungsverfahren anwenden wollen würden, müssten wir unsere zweite Gleichung vorher noch durch 2 teilen. Unsere beiden Gleichungen hätten dann die folgende Gestalt:
\begin{align*}
\begin{array}{rrcll}
\textrm{I} & 4x &=&5-y & \\
\textrm{II} & 8x &=& 10-2y & |:2 \\ &&&& \\
\textrm{I} & 4x &=&5-y & \\
\textrm{II} & 4x &=& 5-y &
\end{array}
\end{align*}
Nun sehen wir, dass unsere beiden Gleichungen identisch sind. Trotzdem wollen wir gucken was passiert, wenn wir die Terme gleichsetzen und einfach weiter rechnen:
\begin{align*}
\begin{array}{rcll}
5-y &=&5-y & | -5 \\
-y &=& -y & | +y \\
0 & = & 0 &
\end{array}
\end{align*}
Wir erhalten also eine wahre Aussage, denn 0 ist gleich 0. Falls unsere beiden Geraden identisch sein sollten, muss eine wahre Aussage herauskommen.
LGS lösen mit Additionsverfahren
Vorgehen:
- Entscheide, welche Unbekannte du eliminieren willst.
- Überlege, was du tun musst, damit die Unbekannte wegfällt.
- Berechne die Unbekannten.
Beispiel für ein quadratisches Gleichungssystem mit 2 Gleichungen und 2 Unbekannten:
\begin{align*}
\text{I} \ \ 2x_1 + 3x_2 &= 12 \\
\text{II} \quad \ \ x_1 – x_2 &= 1
\end{align*}
Entscheide, welche Unbekannten elimiert werden soll!
Möglichkeit 1: $x_1$ eliminieren, dass schaffen wir indem wir $\text{I}-2\cdot \text{II}$ rechnen.
Möglichkeit 2: $x_2$ eliminieren, dass schaffen wir indem wir $\text{I}+3\cdot \text{II}$ rechnen.
Hier zeigen wir euch Möglichkeit 1:
\begin{align*}
\begin{array}{rrcll}
\text{I} & 2x_1 + 3x_2 &=& 12 & \\
\text{II} & x_1 – x_2 &=& 1 & |\cdot (-2) \\ &&&& \\
\text{I} & 2x_1 + 3x_2 &=& 12 & \\
\text{IIa} &-2x_1 + 2x_2 &=& -2 & |\text{I}+\text{II}a \\ &&&& \\
\text{I} &2x_1 + 3x_2 &=& 12 & \\
\text{IIb} & 5x_2 &=& 10 & \Rightarrow x_2=2
\end{array}
\end{align*}
Zuletzt setzen wir $x_2=2$ in eine der beiden ursprünglichen Zeilen (also $\text{I}$ oder $\text{II}$) ein, um $x_1$ zu berechnen. Wir setzen in $\text{II}$ ein und erhalten:
\begin{align*}
x_1-x_2 & =1 \quad \textrm{mit}~x_1=3 \\
x_1-2 & =1 \quad |+2 \\
x_1 & =3
\end{align*}
Daniel zeigt dir, wie du mit dem Additionsverfahren LGS lösen kannst.
Gauß-Algorithmus
Gegeben sei das Gleichungssystem
\begin{align*} x_1 – x_2 + 2x_3 &= 0 \\ -2x_1 + x_2 – 6x_3 &= 0 \\ x_1 – 2x_3 &= 3 \\ \end{align*}
Unter dem „Lösen linearer Gleichungssysteme“ versteht man die Berechnung von Unbekannten – in diesem Fall von $x_1$, $x_2$ und $x_3$. Da zum Lösen eines Gleichungssystems meist mehrere Schritte notwendig sind, wird es irgendwann lästig, bei jedem Schritt das ganze Gleichungssystem nochmal abzuschreiben. Aus diesem Grund lassen wir die Unbekannten ($x_1$,$x_2$,$x_3$) weg und schreiben nur die Koeffizienten auf.
Statt
\begin{align*} x_1 – x_2 + 2x_3 &= 0 \\ -2x_1 + x_2 – 6x_3 &= 0 \\ x_1 – 2x_3 &= 3 \\ \end{align*}
schreiben wir
\begin{align*} \begin{array}{rrr|c} x_1 & x_2 & x_3 & r. S. \\ \hline 1 & -1 & 2 & 0\\ -2 & 1 & -6 & 0\\ 1 & 0 & -2 & 3 \end{array} \end{align*}
Dabei steht „r. S.“ für die rechte Seite des Gleichungssystems. Das ist der Teil, der rechts von dem Gleichheitszeichen steht. Wir erhalten also die Koeffizientenschreibweise des LGS.
Ziel des Gauß-Algorithmus ist es, mit Hilfe von zeilenweisen Umformungen (dazu gleich mehr) unter der Hauptdiagonalen Nullen zu erzeugen. Was zunächst sehr abstrakt klingt, ist eigentlich gar nicht so schwierig. Nach einigen Umformungen sieht das Gleichungssystem so aus:
\begin{align*}
\begin{array}{rrr|c} x_1 & x_2 & x_3 & r. S. \\ \hline 1 & -1 & 2 & 0\\ 0& -1 & -2 & 0\\ 0& 0 & -6 & 3 \end{array}
\end{align*}
Doch was hat uns diese Umformung gebracht? Erst wenn wir wieder unsere Unbekannten einfügen, wird deutlich, was uns diese Nullen bringen.
\begin{align*} x_1 – x_2 + 2x_3 &= 0 \\ -x_2 – 2x_3 &= 0 \\ -6x_3 &= 3 \\ \end{align*}
Ist das Gleichungssystem so umgeformt, dass unter der Hauptdiagonalen nur noch Nullen sind, kann man die Unbekannten ganz leicht berechnen.
Wie komme ich aber auf die Nullen? Um die Nullen zu berechnen, darf man Zeilen
- vertauschen
- mit einer Zahl multiplizieren
- durch eine Zahl dividieren
- addieren
- subtrahieren
Hier die schrittweise Lösung unseres Beispiels: Um die Null in der 3. Zeile und 1. Spalte zu erhalten, betrachten wir zunächst unser Ausgangsgleichungssystem.
\begin{align*}\begin{array}{rrr|c} 1 & -1 & 2 & 0\\ -2 & 1 & -6 & 0\\ 1 & 0 & -2 & 3 \end{array} \end{align*}
Scharfes Hinsehen verrät, dass wir unsere dritte Zeile von der ersten Zeile abziehen müssen. Ausführlich:
\begin{align*}
\begin{array}{rrr|l} 1 & 0 & -2 & 3 \qquad \text{3. Zeile}\\ 1 & -1 & 2 & 0 \qquad \text{1. Zeile}\\ \hline 0 & 1 & -4 & 3 \qquad \text{3. Zeile – 1. Zeile} \end{array}
\end{align*}
Unser Gleichungssystem sieht nach dem ersten Schritt also wie folgt aus:
\begin{align*}
\begin{array}{rrr|l} 1 & -1 & 2 & 0 \qquad \text{1. Zeile}\\ -2 & 1 & -6 & 0 \qquad \text{2. Zeile}\\ 0 & 1 & -4 & 3 \qquad \text{3. Zeile*} \end{array}
\end{align*}
Das $*$ zeigt uns, das es sich um eine neue Zeile handelt. Um die Null in der 2. Zeile und 1. Spalte zu erhalten, addieren wir zu der 2. Zeile zweimal die 1. Zeile:
\begin{align*}
\begin{array}{rrr|l} -2 & 1 & -6 & 0 \qquad \text{2. Zeile}\\ 2 & -2 & 4 & 0 \qquad \text{\(2 \cdot\) 1. Zeile}\\ \hline 0 & -1 & -2 & 0 \qquad \text{2. Zeile + \(2 \cdot\) 1. Zeile} \end{array}
\end{align*}
Unser Gleichungssystem sieht nach dem zweiten Schritt also wie folgt aus:
\begin{align*}
\begin{array}{rrr|l} 1 & -1 & 2 & 0 \qquad \text{1. Zeile}\\ 0 & -1 & -2 & 0\qquad \text{2. Zeile*}\\ 0& 1 & -4 & 3 \qquad \text{3. Zeile} \end{array}
\end{align*}
Um die Null in der 3. Zeile und 2. Spalte zu erhalten, addieren wir zu der 3. Zeile die 2. Zeile und es folgt
\begin{align*}
\begin{array}{rrr|l} 1 & -1 & 2 & 0 \qquad \text{1. Zeile}\\ {\color{}0}& -1 & -2 & 0\qquad \text{2. Zeile}\\ {\color{}0}& {\color{}0}& -6 & 3\qquad \text{3. Zeile*} \end{array}
\end{align*}
Da die Nullen unter der Hauptdiagonalen berechnet sind, haben wir unser Ziel erreicht. Wie man jetzt die Unbekannten berechnet, wurde bereits oben erklärt.
Merke:
- Reihenfolge bei der Berechnung der Nullen spielt eine wichtige Rolle.
- Zuerst muss man die beiden Nullen in der ersten Spalte berechnen – welche der beiden Nullen man zuerst berechnet, ist jedoch egal. Anschließend berechnet man die verbleibende Null in der zweiten Spalte.
- Falls in der ersten Zeile (der ersten Spalte!) bereits eine Null vorliegt, lohnt es sich die Zeilen entsprechend zu vertauschen, um sich die Berechnung einer Null zu sparen.
NEU
Textaufgaben zu linearen Gleichungssystemen
Zum Thema lineare Gleichungssysteme wollen wir uns die folgende Textaufgabe angucken:
Auf einem Bauernhof leben Schweine und Hühner. Insgesamt gibt es $180$ Tiere, welche zusammen $520$ Beine haben. Wie viele Schweine bzw. Hühner leben auf dem Bauernhof?
Als erstes machen wir uns klar, dass unsere beiden Variablen $x$ und $y$ eindeutig zugeordnet werden müssen. In diesem Beispiel ist die folgende Zuordnung hilfreich:
- $x$: Anzahl der Schweine auf dem Bauernhof
- $y$: Anzahl der Hühner auf dem Bauernhof
Durch diese Zuordnung ergibt sich auch schon die erste Gleichung für unser lineares Gleichungssystem, nämlich:
\[x+y=180\]
Zur Erklärung, die Anzahl der Schweine $x$ addiert mit der Anzahl der Hühner $y$ müssen zusammen $180$ ergeben, also die Anzahl aller Tiere auf dem Bauernhof.
Des Weiteren stellen wir fest, dass Schweine Vierbeiner und Hühner Zweibeiner sind. Also ist die Anzahl der Schweine multipliziert mit $4$ und die Anzahl der Hühner multipliziert mit $2$ unsere Gesamtanzahl aller Beine auf dem Bauernhof, nämlich 520. Unsere zweite Gleichung lautet also:
\[4x+2y=520\]
Unsere beiden Gleichungen schreiben wir jetzt noch einmal geordnet direkt untereinander und lösen das lineare Gleichungssystem dann mit Hilfe des Einsetzungsverfahrens:
\begin{align*}
\begin{array}{rrcll}
\text{I} & x + y &=& 180 & \\
\text{II} & 4x+2y &=& 520 &
\end{array}
\end{align*}
Wir stellen die erste Gleichung nach $y$ um und setzen den entstandenen Term in die zweite Gleichung ein:
\begin{align*}
\begin{array}{rrcll}
\text{I} & x + y &=& 180 & | -x \\
\text{II} & 4x+2y &=& 520 & \\ &&&& \\
\text{I} & y &=& 180 – x & \\
\text{IIa} &4x + 2y &=& 520 &
\end{array}
\end{align*}
Jetzt können wir das $y$ aus Gleichung I in Gleichung II einsetzen:
\begin{align*}
\begin{array}{rcll}
4x+2\cdot (180-x) &=& 520 & \\
4x+360-2x &=& 520 & \\
2x+360 &=& 520 & | -360 \\
2x &=& 160 & | :2 \\
x&=&80 &
\end{array}
\end{align*}
Jetzt wissen wir also schon einmal, dass $80$ Schweine auf dem Bauernhof leben. Als nächstes setzen wir $x=80$ in die obere Gleichung (Gleichung I) ein, um unsere Anzahl der Hühner zu berechnen:
\[y=180-80=100\]
Es leben demnach 80 Schweine und 100 Hühner auf dem Bauernhof.
Wir kontrollieren unsere Lösung mit Gleichung II:
$4x+2y=4\cdot 80+2\cdot 100=320+200=520 $ ✔
Beispielaufgabe 1) Lineare Gleichungssysteme
Löse das folgende Gleichungssystem mit einem geeigneten Verfahren:
$I: \ 2y-4x=3$
$II: \ x=y+4$
Schau dir zur Vertiefung Daniels beiden Videos zum LGS lösen mit Gauß-Algorithmus an!


