
ln-Funktion
Eine Funktion heißt Logarithmusfunktion (zur Basis $a$), wenn sie allgemein die Form
\begin{align}
f(x) = log_a(x), \ x \in (0,\infty)
\end{align}
aufweist, wobei $a$ eine beliebige positive Konstante bezeichnet.
In den speziellen Fällen $a = e$, $a = 10$ und $a = 2$ spricht man von
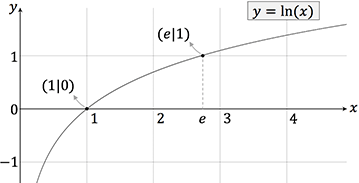
- $f(x)= \ln(x)$, als „natürlichen Logarithmus“,
- $f(x) = lg(x)$, als „dekadischen Logarithmus“ bzw.
- $f(x) = ld(x)$, als „dyadischen Logarithmus“.
In der Regel rechnen wir aber mit dem natürlichen Logarithmus. Falls aber mal der Fall auftreten sollte – und das könnte er – dass kein natürlicher Logarithmus vorliegt, kann dieser mit einfachen Mitteln wie folgt umgeschrieben werden:
\begin{align*}
log_a(x)=\frac{\ln(x)}{\ln(a)}
\end{align*}
Ein weiterer nützlicher Zusammenhang ist
\begin{align*}
e^{\ln(x)}=x \ \textrm{bzw.} \ \ln(e^x)=x,
\end{align*}
der gerade im Bereich „Lösen von Gleichungen“ äußerst wichtig ist.
Neu!
Logarithmengesetze
- $\ln(ab)=\ln(a)+\ln(b)$
- $\ln(\frac{a}{b})=\ln(a)-\ln(b)$
- $\ln(a^b)=b\cdot \ln(a)$
Schau dir zur Vertiefung Daniels Video zum Thema ln-Funktion an.
Untersuchung von ln-Funktion
Bei Logarithmusfunktionen ist oft der maximale Definitionsbereich stark eingeschränkt und das Verhalten der Funktionen
an den Rändern des Definitionsbereiches nicht unmittelbar ersichtlich. Besonders beim Ableiten können Umformungen des Funktionsterms die Anwendung von aufwändigeren Ableitungsregeln vermeiden.
Grundlagen
- Da $\ln(x)$ nur für $x>0$ definiert ist, wird zuerst die Definitionsmenge von $f$ bestimmt.
- Wichtige Punkte der Funktion $\ln(x)$ sind $\ln(1)=0$ und $\ln(e)=1$.
- Den Funktionsterm $f(x)$ kann man mit den Logarithmengesetzen, die wir schon kennengelernt haben,
eventuell vereinfachen. - Für $x \to 0$ strebt $\ln(x) \to – \infty$.
Für $x \to + \infty$ strebt $\ln(x) \to + \infty$.
In Daniels Playlist zur ln-Funktion findest du viele weitere Lernvideos.

