
Schwerpunkt berechnen
Berechnung mit dem Tabellenverfahren
Das Tabellenverfahren ist praktisch bei der Schwerpunktberechnung von zusammengesetzten Flächen. Hinweis: Alle Angaben sind in cm.
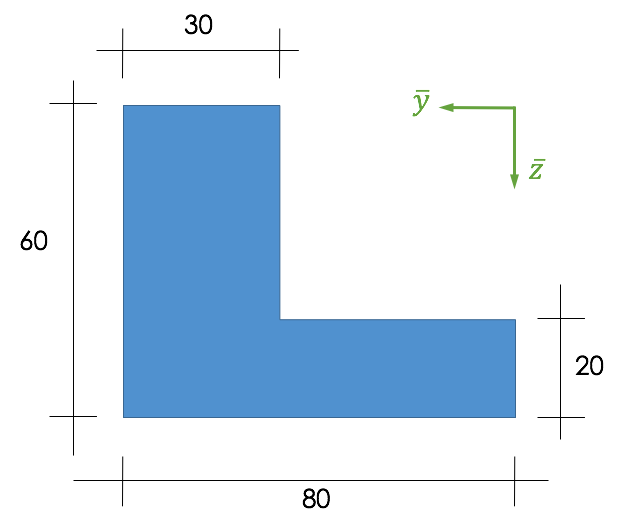
Vorgehen
- Flächenunterteilung in einfache Formen, z.B. Rechtecke, Kreise, Dreiecke
- Teilschwerpunkte bestimmen
- Teilflächen bestimmen
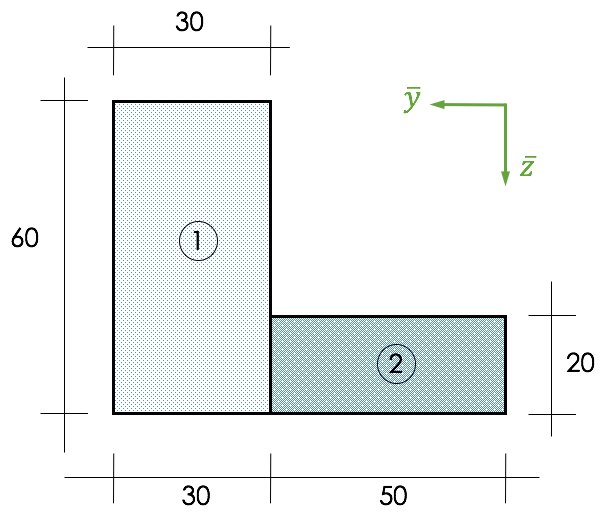
Gleichungen tabellarisch auswerten und Schwerpunkt bestimmen!
Beachte, dass man immer ein Referenzkoordinatensystem (hier: $\bar{y}-\bar{z}$) haben muss, worauf man sich bezieht. Das ist in der Regel gegeben! Das Schwerpunkt-Koordinatensystem wird mit $y-z$ bezeichnet.

19,99€
Warum $y-z$ und nicht $x-y$? In der Regel liegt die $x$-Achse entlang des Bauteils. Stellt euch einen Balken vor und dann guckt ihr euch den Querschnitt des Balkens an. Dann guckt ihr auf die $x$-Achse und seht das $y-z$-Koordinatensystem nach dem Rechtssystem.
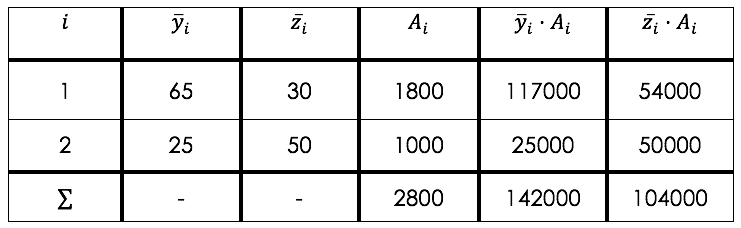
Gleichung für die Berechnung der Schwerpunktkoordinaten:
\begin{align*}
\bar{y}_s = \frac{\sum \bar{y}_i \cdot A_i}{\sum A_i} \quad \textrm{und} \quad \bar{z}_s = \frac{\sum \bar{z}_i \cdot A_i}{\sum A_i}
\end{align*}
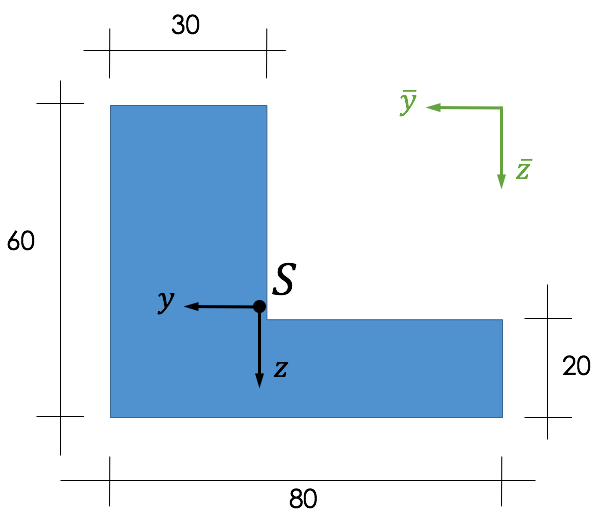
Die Lage des Schwerpunktes ist in diesem Fall bei:
\begin{align*}
\bar{y}_s = \frac{142000}{2800} \approx 50,71 \ \textrm{cm} \quad \textrm{und} \quad \bar{z}_s = \frac{104000}{2800} \approx 37,14 \ \textrm{cm}
\end{align*}
Ausgehend von dem $\bar{y}-\bar{z}$-Koordinatensystem kann der Schwerpunkt eingetragen werden. In dem Schwerpunkt findet sich dann das Schwerpunktkoordinatensystem $y-z$.
Video Schwerpunkt berechnen mit Tabellenverfahren
Video Schwerpunkt berechnen mit Tabellenverfahren (ausgestanzte Fläche
Video Schwerpunkt mit Integral bestimmen

