
Abstandsberechnung
In diesem Artikel zeigen wir dir wie du Abstände in der Vektorrechnung ermittelst:
- Abstand Punkt zu Punkt
- Abstand Punkt zu Gerade
- Berechnung mit der Hilfsebene
- Abstand paralleler Geraden
- Abstand windschiefer Geraden
- Berechnung mit dem Lotverfahren
- Abstand Punkt zu Ebene
- Abstandsberechnung mit Hesseform
1,99€
Abstand Punkt zu Punkt
Vorgehen:
- Vektor $\overrightarrow{AB}$ der beiden gegebenen Punkte $A$ und $B$ berechnen.
- Länge des Vektors $\overrightarrow{AB}$ mit dem Betrag berechnen: Abstand = $|\overrightarrow{AB}|$
Daniel erklärt euch nochmal das Thema Punkt zu Punkt
Abstand Punkt zu Gerade
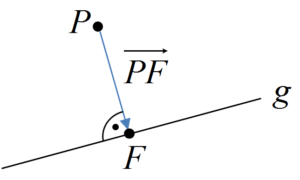
Der Abstand $d$ eines Punktes $P$ von einer Geraden $g$ ist gleich der Länge des Lotes von $P$ auf $g$; d.h. $d$ ist gleich dem Betrag des Vektors $\overrightarrow{PF}$, wobei $F$ der Lotfusspunkt ist.
Hinweis: Unter Umständen ist es sinnvoll vorher zu überprüfen, ob der Punkt auf der Geraden liegt. Der Abstand wäre dann logischerweise 0 und man spart sich viel Rechenarbeit!
Lotverfahren
Gegeben sei eine Gerade $g$ in Parameterform und ein Punkt $P = (3|3|3)$ mit \begin{align*} g:\vec{x} = \left( \begin{array}{c} 2 \\1 \\ 1 \end{array} \right) + t \cdot \left( \begin{array}{c} 2 \\ -1 \\ -1 \end{array} \right) \notag \end{align*}
Wir wissen, dass der Lotfußpunkt auf der Geraden $g$ liegen soll. Also gilt zunächst allgemein $F(2+2t |1-1t|1-1t)$. Die Gerade durch den Punkt $P$ und $F$ muss senkrecht (orthogonal) zur Geraden $g$ sein. Daher muss das Skalarprodukt Null sein!
\begin{align*}
\overrightarrow{PF} \bullet \overrightarrow{RV_g} = 0 \notag
\end{align*}
Es folgt:
\begin{align*}
\overrightarrow{PF} = \left( \begin{array}{c} 2+2t \\ 1-1t \\ 1-1t \end{array} \right) – \left( \begin{array}{c} 3 \\ 3 \\ 3 \end{array} \right) = \left( \begin{array}{c} -1+2t \\ -2-1t \\ -2-1t \end{array} \right) \Rightarrow \left( \begin{array}{c} -1+2t \\ -2-1t \\ -2-1t \end{array} \right) \bullet \left( \begin{array}{c} 2 \\ -1 \\ -1 \end{array} \right) = 0 \notag
\end{align*}
Das Ergebnis lautet $t=-1/3$ und damit kann der Lotfußpunkt $F$ bestimmt werden. Anschließend bestimmen wir den Abstand der beiden Punkte $P$ und $F(4/3|4/3|4/3): d=|\overrightarrow{PF}| \approx 2,89$.
Daniel erklärt euch in seinem Lernvideo das Lotfußpunktverfahren.
Berechnung mit der Hilfsebene
Als Alternative zum Lotverfahren, kann der Abstand des Punktes zu einer Geraden auch mit einer Hilfsebene berechnet werden.
Die Idee: Eine Hilfsebene $E$ konstruieren, die den Abstandspunkt $P$ enthält und von der Geraden $g$ senkrecht durchstoßen wird.
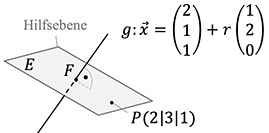
Vorgehen:
- Richtungsvektor der Geraden $g$ ist Normalenvektor $\vec{n}$ der Hilfsebene $E$.
- Koordinatenform von $E$ mit $\vec{n}$ und $P$ aufstellen.
- Durchstoßpunkt $F$ von $g$ und $E$ bestimmen.
- Abstand von $P$ zu Durchstoßpunkt $F$ berechnen.
Für unser Beispiel folgt mit dem Normalenvektor $\vec{n}=(1 \ 2 \ 0)^T$ und dem Ansatz
\begin{align*}
E: \ \vec{n} \bullet \vec{x} = \vec{n} \bullet \vec{p} \quad \Leftrightarrow \quad
\begin{pmatrix}
1 \\ 2 \\ 0
\end{pmatrix} \bullet \begin{pmatrix}
x_1 \\ x_2 \\ x_3
\end{pmatrix} = \begin{pmatrix}
1 \\ 2 \\ 0
\end{pmatrix} \bullet \begin{pmatrix}
2 \\ 3 \\ 1
\end{pmatrix}
\end{align*}
die Koordinatenform der Hilfsebene $x_1 + 2x_2=8$. Um den Durchstoßpunkt (oder Schnittpunkt) zu berechnen, setzen wir die Gerade in die Koordinatenform der Hilfsebene ein und erhalten:
\begin{align*}
(2+r) + 2(1+2r) =8 \quad \Rightarrow \quad r=\frac{4}{5}
\end{align*}
Anschließend setzen wir $r=\frac{4}{5}$ in die Gerade $g$ ein und erhalten den Durchstoßpunkt $F(\frac{14}{5}|\frac{13}{5}|1)$. Der Abstand ist dann $d=|\overrightarrow{PF}| \approx 0,89$.
Schau dir zur Vertiefung Daniels Lernvideo zum Thema Abstand Punkt-Gerade an!
Abstand paralleler Geraden
Mit Abstand ist hier die kürzeste Strecke zwischen zwei Geraden gemeint. Der Abstand zweier paralleler Geraden $g_1$ und $g_2$ ist der Abstand eines beliebigen Punktes $P \in g_2$ von der Geraden $g_1$.
Vorgehen:
- Ortsvektor der Geraden $g_2$ wird als Punkt $P$ festgelegt
- weiter mit dem Vorgehen Abstand Punkt zu Gerade
Abstand windschiefer Geraden
Bei der Berechnung des Abstands zweier windschiefer Geraden werden wir in diesem Abschnitt zwei Verfahren kennenlernen. Zum einen die Verwendung einer Hilfsebene und zum anderen die Verwendung von Lotfußpunkten.
Berechnung mit Hilfsebene
Wir betrachten die beiden windschiefen Geraden $g$ und $h$. Zur Berechnung des Abstands führen wir eine Hilfsebene $E$ ein, wodurch wir später nur noch den Abstand eines Punktes $P$ von der Ebene berechnen müssen.
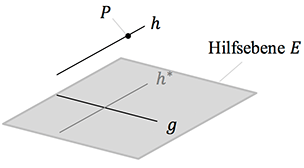
Vorgehen:
- Normalenvektor $\vec{n}$ mit Richtungsvektoren der Geraden $g$ und $h$ bestimmen.
- Koordinatenform von $E$ aufstellen, z.B. mit Punkt von $g$ und $\vec{n}$.
- Abstand des Punktes (Ortsvektor nehmen!) von der Geraden $h$ zur Hilfsebene $E$ bestimmen.
Beispiel
Berechne den Abstand $d$ der beiden windschiefen Geraden
\begin{align*}
g:\ \vec{x} = \begin{pmatrix} -7 \\ 2 \\ -3 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} \quad \textrm{und} \quad
h:\ \vec{x} = \begin{pmatrix} -3 \\ -3 \\ 3 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}
\end{align*}
Zunächst berechnen wir den Normalenvektor mit dem Kreuzprodukt:
\begin{align*}
\begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} \times \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1-4 \\ 2-0 \\ 0-1 \end{pmatrix} = \begin{pmatrix} -3 \\ 2 \\ -1 \end{pmatrix} = \vec{n}
\end{align*}
Die Koordinatenform der Hilfsebene $E$ erhalten wir mit dem Ansatz $\vec{n} \bullet \vec{x} = \vec{n} \bullet \vec{p}$:
\begin{align*}
\begin{pmatrix} -3 \\ 2 \\ -1 \end{pmatrix} \bullet \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} -3 \\ 2 \\ -1 \end{pmatrix} \bullet \begin{pmatrix} -7 \\ 2 \\ -3 \end{pmatrix} \quad \Rightarrow \quad -3x_1 + 2x_2 – x_3 = 28
\end{align*}
Um den gesuchten Abstand zu bestimmen, wählen wir einen beliebigen Punkt $P$ der Geraden $h$ aus. Am einfachsten ist der Ortsvektor, hier $(-3 \ -3 \ 3)^T$. Anschließend berechnen wir den Abstand des Punktes $P$ zur Ebene $E$ mit der Hesseform:
\begin{align*}
d(P;E) &=\left| \frac{-3x_1+2x_2-x_3-28}{|\vec{n}|}\right| = \left| \frac{-3 \cdot (-3) + 2 \cdot (-3) – 3 – 28}{\sqrt{14}} \right| \approx 7,48
\end{align*}
1,99€
Berechnung mit dem Lotverfahren
Gegeben seien die Geraden
\begin{align*}
g: \ \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \quad \textrm{und} \quad
h:\ \vec{x} = \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} + s \cdot \begin{pmatrix} -2 \\ 1 \\ 1 \end{pmatrix},
\end{align*}
welche windschief zueinander sind. Um den kürzesten Abstand der Geraden zu bestimmen, kann man auch mit Hilfe des Lotverfahrens arbeiten. Gesucht ist die Verbindungslinie zwischen zwei Punkten, z.B. $G$ und $H$, welche senkrecht zur Geraden $g$ und gleichzeitig auch senkrecht zu Geraden $h$ verläuft.
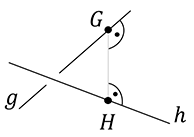
Daraus ergeben sich zwei Bedingungen, denn zwei Vektoren sind senkrecht zueinander, wenn das Skalarprodukt gleich 0 ist. Es muss gelten:
\begin{align*}
\textrm{I} \quad \overrightarrow{GH} \bullet \overrightarrow{RV}_g = 0 \\
\textrm{II} \quad \overrightarrow{GH} \bullet \overrightarrow{RV}_h = 0
\end{align*}
Für die Bestimmung der Verbindungslinie $\overrightarrow{GH}$ (auch möglich: $\overrightarrow{HG}$) merken wir uns: Gerade $h$ minus Gerade $g$.
\begin{align*}
\overrightarrow{GH} = \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} + s \cdot \begin{pmatrix} -2 \\ 1 \\ 1 \end{pmatrix} – \left[ \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \right] = \begin{pmatrix} -1 \\ -1 \\ 1 \end{pmatrix} + s \cdot \begin{pmatrix} -2 \\ 1 \\ 1 \end{pmatrix} – r \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}
\end{align*}
Einsetzen von $\overrightarrow{GH}$ und der Richtungsvektoren von $g$ und $h$ in die Bedingungen I, II liefert folgendes Gleichungssystem:
\begin{align*}
\textrm{I}& \quad -2r-s=0 \\
\textrm{II}& \quad 6s + r =-2
\end{align*}
Wir erhalten nach dem Lösen des Gleichungssystems für $r=2/11$ und $s=-4/11$. Die Werte setzen wir anschließend in die Geradengleichungen von $g$ und $h$ ein und erhalten die Punkte $G=(24/11 \ | \ 1 \ | \ -13/11)$ und $H=(19/11 \ | \ -4/11 \ | \ 18/11)$. Der Abstand ist dann nichts anderes als der Betrag des Vektors $\overrightarrow{GH}= 1,51 [LE]$.
Schau dir dazu das Lernvideo zu „Abstand windschiefer Geraden“ an!
Abstand Punkt zu Ebene
In diesem Abschnitt lernen wir zwei Verfahren, wie die Berechnung des Abstands von einem Punkt zu einer Ebene erfolgen kann.
Zum Einstieg schaust du dir am besten das Lernvideo zum Lotfußpunktverfahren an.
Um den Abstand mit dem Lotverfahren oder Lotfußpunktverfahren zu ermitteln, müssen wir wissen, wie man einen Schnittpunkt oder Durchstoßpunkt von Gerade und Ebene sowie den Abstand zweier Punkte berechnet. Es empfiehlt sich, die Ebenengleichung in Koordinatenform vorliegen zu haben!
Vorgehen:
- Lotgerade $g$ mit Normalenvektor der Ebene und Ortsvektor $\overrightarrow{0P}$ aufstellen.
- Schnittpunkt $F$ von Lotgerade mit Ebene berechnen (Lotfußpunkt).
- Abstand vom Punkt zum Schnittpunkt berechnen (entspricht dem Abstand vom Punkt zur Ebene).
Beispiel
Gegeben sei die Ebene $E: 2x_1 – x_2 + x_3 = 8$ und der Punkt $P(2|1|3)$. Berechne den Abstand mit einer Hilfsgeraden (Lotgerade).
Wir stellen zunächst die Hilfsgerade $g$ auf, die durch Punkt $P$ und senkrecht zur Ebene $E$ verläuft:
\begin{align*}
g: \vec{x} = \underbrace{\left( \begin{array}{c} 2 \\ 1 \\ 3 \end{array} \right)}_{P} + \ t \cdot
\underbrace{\left( \begin{array}{c} 2 \\ -1 \\ 1 \end{array} \right)}_{\vec{n}}, \notag
\end{align*}
wobei der Richtungsvektor dem Normalenvektor $\vec{n}$ der Ebenengleichung entspricht. Nun kann der Lotfußpunkt $F$ bestimmt werden (Thema: Schnittpunkt Gerade und Ebene), indem wir die einzelnen Koordinaten der Gerade rausschreiben und in die Ebenengleichung einsetzen:
\begin{align*}
x_1 &= 2 + 2 \cdot t \\
x_2 &= 1 – 1 \cdot t \quad \quad \Rightarrow 2 \cdot (2 + 2 \cdot t) – 1\cdot (1 – 1 \cdot t) + 1\cdot (3 + 1\cdot t)=8 \\
x_3 &= 3 + 1 \cdot t
\end{align*}
Wir erhalten für $t=1/3$ und setzen diesen Wert in die Geradengleichung ein um den Lotfußpunkt $F=(8/3 \ | \ 2/3 \ | \ 10/3)$ zu erhalten. Anschließend berechnen wir den Abstand der beiden Punkte $P$ und $F$ mit $|\overrightarrow{PF}|\approx 0,82$.
1,99€
Erklärvideo mit Hesseform
Wenn es nur um den Abstand geht und nicht Lotfußpunkte berechnet werden sollen, ist die Abstandsberechnung mit der Hesseform am leichtesten. Hierbei sollte vor allem die Umwandlung von Ebenengleichungen bekannt sein. Dazu betrachten wir das nebenstehende Beispiel.
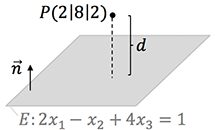
Vorgehen:
- Ebenengleichung auf Koordinatenform bringen, falls nicht schon gegeben. Hier: $2x_1-x_2+4x_3=1$
- Normalenvektor ablesen und Länge bestimmen. Hier: $\vec{n} = (2 \ -1 \ 4)^T$ und $|\vec{n}| = \sqrt{21}$
- Ebenengleichung umstellen: $2x_1-x_2+4x_3-1=0$
- Punkt $P$ und Ebene $E$ in die Hesseform einsetzen: \begin{align*} d(P,E)= \left| \frac{2x_1-x_2+4x_3-1}{\vec{|n|}} \right| = \left| \frac{2 \cdot 2 – 1\cdot 8 +4 \cdot 2 -1}{\sqrt{21}} \right| \approx 0,65 \end{align*}
Lass dir nochmals von Daniel das Thema „Abstand Punkt-Ebene“ erklären!
