
Abbildungen
Ein zentrales Konzept der Mathematik ist die Abbildung, die auch Funktion genannt wird. Abbildungen sind eindeutige Zuordnungen zwischen zwei Mengen $D$ und $Z$. Dies bedeutet, dass jedem Element $x\in D$ durch die Abbildung $f$ genau ein Element $f(x)\in Z$ zugeordnet wird.
themen zu Abbildungen auf dieser Seite
- Mögliche Abbildungen
- Punkte abbilden
- Bildgerade bestimmen
- Fixpunkt bestimmen
- Fixpunktgerade bestimmen
- Fixgeraden bestimmen
- Verkettung von Abbildungen
- Abbildungsgleichung bestimmen
Neu!
Mögliche Abbildungen
Ein bisher in der Schule eher selten behandeltes Thema sind die Abbildungen der Ebene und des Raumes. Darunter versteht man zum Beispiel Drehungen, Verschiebungen und Spiegelungen, die in der Mittelstufe rein zeichnerisch in der Ebene untersucht werden. Diese Abbildungen kann man natürlich auch rechnerisch darstellen, und zwar nicht nur in der Ebene, sondern auch im Raum. Geeignetes Mittel dafür sind Matrizen.
Wir werden uns hier nur lineare Abbildungen ansehen. Im Folgenden werden wir auf die bekanntesten Abbildungen in der Schulmathematik eingehen:
1. Spiegelungen
an einer Koordinatenachse
Wenn man einen Punkt $P(x|y)$ spiegelt, bleibt die $x$-Koordinate wie sie ist, und bei der $y$-Koordinate dreht sich das Vorzeichen um. Bildpunkte bezeichnet man üblicherweise mit $P‘$, die Koordinaten entsprechend mit $x‘$ und $y‘$.
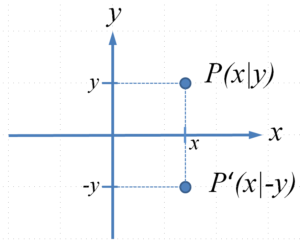
Für die Spiegelung an der $x$-Achse gilt somit
\begin{align*}
x‘ = x \quad \textrm{und} \quad y‘ = y
\end{align*}
Diese Gleichungen bezeichnet man als Abbildungsgleichungen. Sie stellen die Beziehung zwischen den ursprünglichen Koordinaten und den Bildkoordinaten her, genauer: sie geben an, wie man die Koordinaten des Bildpunktes aus den Koordinaten des Urbildpunktes berechnet.
Die Abbildungsgleichungen sollen nun mit Hilfe einer Matrix dargestellt werden. Dazu schreiben wir zunächst etwas ausführlicher:
\begin{align*}
x‘ = 1\cdot x + 0 \cdot y \quad &\textrm{und} \quad y‘ = 0 \cdot x – 1 \cdot y \quad \textrm{bzw. in Matrixform} \\
\begin{pmatrix} x‘ \\ y‘ \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} \quad &\textrm{oder} \quad \vec{x‘} = A \cdot \vec{x} \quad \textrm{mit} \quad A= \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}
\end{align*}
Die Schreibweise inklusive des Vektors $x$ heißt Abbildungsgleichung, die Matrix $A$ Abbildungsmatrix.
am Ursprung
Bei der Punktspiegelung am Ursprung drehen sich die Vorzeichen beider Koordinaten um:
\begin{align*}
x‘ &= -x = -1 \cdot x+ 0\cdot y \\
y‘ &= -y = 0\cdot x – 1\cdot y
\end{align*}
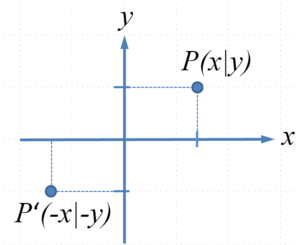
Die Abbildungsmatrix der Punktspiegelung am Ursprung hat damit die Gestalt
\begin{align*}
A= \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}
\end{align*}
an einer beliebigen Ursprungsgeraden
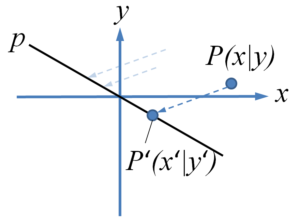
Die Spiegelung wird in der Schule immer orthogonal (rechtwinklig) zur Spiegelachse durchgeführt. Die Zeichnung lässt bereits ahnen, dass man ähnlich wie bei der Projektion vorgeht: man berechnet zunächst den Schnittpunkt mit der Geraden.
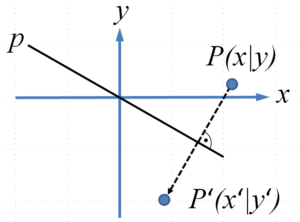
Da man jetzt den Weg vom Urbildpunkt $P$ zur Geraden sozusagen zweimal laufen muss, um den Bildpunkt $P‘$ zu erhalten, verdoppelt man einfach den Parameter aus der Geradengleichung.Der Punkt $P(x|y)$ soll an der Geraden bzw. Achse $p: x + 3y = 0$ gespiegelt werden. Zunächst stellen wir eine Gerade auf. Da unsere Hilfsgerade (gestrichelte Linie im Bild) senkrecht auf der Achse stehen soll, verwendet man als Richtungsvektor den Normalenvektor $\vec{n}=(1,3)^T$ und muss somit den Schnittpunkt von
\begin{align*}
p: x + 3y = 0 \quad \textrm{und} \quad g:\vec{x‘} = \begin{pmatrix} x \\ y \end{pmatrix} + t \cdot \begin{pmatrix} 1\\ 3 \end{pmatrix}
\end{align*}
berechnen.
Die Geradengleichung $g$ schreiben wir um und ersetzen in der Geradengleichung von $p$ die Variable $x$ durch $x+t$ und $y$ durch $y+3t$:
\begin{align*}
x + t + 3\cdot (y+3t) &= 0 \\
x + t + 3y+9t &= 0 \\
10t &= -x-3y \\
t &= -0,1x-0,3y
\end{align*}
Es ist jetzt nicht nötig, den Schnittpunkt zu berechnen, der ja nur ein Hilfspunkt ist. Stattdessen verdoppelt man den Parameter $t$ und erhält sofort die Koordinaten des Bildpunktes.
\begin{align*}
\vec{x‘} = \vec{x} + 2 \cdot (-0,1x-0,3y) \begin{pmatrix} 1 \\ 3 \end{pmatrix} = \begin{pmatrix}0,8 x – 0,6 y \\ -0,6 x – 0,8 y \end{pmatrix}
\end{align*}
und daraus wiederum die Abbildungsmatrix
\begin{align*}
A= \begin{pmatrix} 0,8 & -0,6 \\ -0,6 & -0,8 \end{pmatrix}
\end{align*}
Neu!
2. Projektion
auf eine Koordinatenachse
Eine weitere einfache Abbildung ist die Projektion auf eine Koordinatenachse, in diesem Beispiel auf die $x$-Achse. Die Abbildungsgleichungen lauten:
\begin{align*}
x‘ &= x = 1 \cdot x + 0\cdot y \\
y‘ &= 0 = 0\cdot x + 0\cdot y
\end{align*}
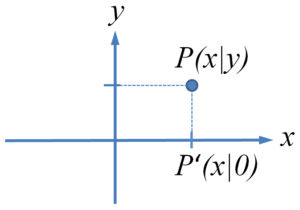
Die Abbildungsmatrix bei Projektion auf die x-Achse lautet also
\begin{align*}
A= \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}
\end{align*}
auf eine beliebige Ursprungsgerade
Die oben vorgeführte Projektion auf die $x$-Achse war senkrecht (orthogonal), aber das ist nicht notwendig. Bei der häufigsten Anwendung in der Schule, dem Schattenwurf, ist das sogar eher die Ausnahme. Dabei wird in eine vorgegebene Richtung auf eine Gerade projiziert. Weil die Strahlen alle parallel verlaufen, nennt man diese Projektion Parallelprojektion.
Die Abbildungsmatrix der Projektion wird in der Schule üblicherweise nicht allgemein angegeben, sondern immer nur für eine spezielle Projektionsgerade und eine spezielle Projektionsrichtung ermittelt. In unserem Beispiel soll ein Punkt $P(x|y)$ in Richtung des Vektors $(2,1)^T$ auf die Gerade $p:x+3y=0$ projiziert werden. Der Punkt $P(x|y)$ muss dennoch die allgemeinen unbekannten Koordinaten behalten, da man für die Berechnung der Abbildungsmatrix die Abbildungsgleichungen in der Form $x‘ = $Zahl$ \cdot x + $Zahl$ \cdot y$ bzw. $y‘ = $Zahl$ \cdot x + $Zahl$ \cdot y$ benötigt.
Der Bildpunkt $P‘$ ist der Schnittpunkt der Projektionsgeraden mit der Geraden durch $P$ in Richtung des vorgegebenen Vektors, also mit
\begin{align*}
g: \vec{x‘} = \begin{pmatrix} x \\ y \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ 1 \end{pmatrix}. n
\end{align*}
Zur Berechnung des Schnittpunktes wird $g$ in die Projektionsgerade $p$ eingesetzt:
\begin{align*}
x + 2t + 3\cdot (y+t) &= 0 \\
x + 2t + 3y+3t &= 0 \\
5t &= -x-3y \\
t &= -0,2x-0,6y
\end{align*}
Setzt man $t$ in die Gerade $g$ ein, so erhält man den Schnittpunkt
\begin{align*}
\begin{pmatrix} x‘ \\ y‘ \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} + (-0,2y-0,6y) \cdot \begin{pmatrix} 2 \\ 1 \end{pmatrix} =
\begin{pmatrix} 0,6x-1,2y \\ -0,2y+0,4y \end{pmatrix}
\end{align*}
und daraus die Abbildungsmatrix $A= \begin{pmatrix} 0,6 & -0,2 \\ -1,2 & 0,4 \end{pmatrix}$.
3. Drehung um den Ursprung
Drehungen erfolgen in der Mathematik immer gegen den Uhrzeigersinn.
Die Herleitung der Drehmatrix soll uns hier nicht interessieren. Sie hat die Gestalt:
\begin{align*}
A=\begin{pmatrix} \cos(\alpha) & -\sin(\alpha) \\ \sin(\alpha) & \cos(\alpha) \end{pmatrix}
\end{align*}
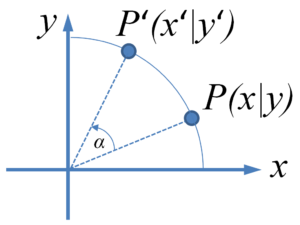
Eine Drehung um den Ursprung um den Winkel $180^\circ$ ist in der Ebene gleichbedeutend mit der Punktspiegelung am Ursprung.
Neu!
Punkte abbilden
Wir wollen einen Punkt $P(2|3)$ mit der Zuordnung
\begin{align*}
\alpha: \vec{x‘} = \begin{pmatrix}
2 & 1 \\ 1 & 3 \end{pmatrix} \cdot \vec{x}
\end{align*}
abbilden. Es gilt
\begin{align*}
\alpha: \vec{x‘} = \begin{pmatrix}
2 & 1 \\ 1 & 3 \end{pmatrix} \cdot \begin{pmatrix}
2 \\ 3
\end{pmatrix} = \begin{pmatrix}
7 \\ 11
\end{pmatrix}.
\end{align*}
Wir erhalten somit den Punkt $P'(7|11)$.
Wir wollen einen Punkt $S(1|4|2)$ mit der Zuordnung
\begin{align*}
\alpha: \vec{x‘} = \begin{pmatrix}
1 & 0 & 1 \\ 2 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \vec{x}
\end{align*}
abbilden. Es gilt
\begin{align*}
\alpha: \vec{x‘} = \begin{pmatrix}
1 & 0 & 1 \\ 2 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix}
1 \\ 4 \\ 2
\end{pmatrix} = \begin{pmatrix}
3 \\ 6 \\ 2
\end{pmatrix}.
\end{align*}
Wir erhalten somit den Punkt $S'(3|6 |2)$.
Schau dir vertiefend dazu Daniels Lernvideo an.
Bildgerade bestimmen
Die Geradengleichung $g$ soll mit $\alpha$ abgebildet werden. Es gilt
\begin{align*}
g: \vec{x} &=\begin{pmatrix} 8 \\ -2 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ 3 \end{pmatrix} \quad \textrm{und} \\
\alpha: \vec{x‘} &=\begin{pmatrix} 3 & -2 \\ 2 & 5 \end{pmatrix} \cdot \vec{x} + \begin{pmatrix} 3 \\ -1 \end{pmatrix}.
\end{align*}
Idee: Wir setzen die Geradengleichung einfach in die Abbildung ein. Es folgt mit
\begin{align*}
\alpha: \vec{x‘} &=\begin{pmatrix} 3 & -2 \\ 2 & 5 \end{pmatrix} \cdot \left( \begin{pmatrix} 8 \\ -2 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ 3 \end{pmatrix} \right) + \begin{pmatrix} 3 \\ -1 \end{pmatrix} \\
&= \begin{pmatrix} 28 \\ 6 \end{pmatrix} + \begin{pmatrix} -9t \\ 13t \end{pmatrix} +\begin{pmatrix} 3 \\ -1 \end{pmatrix} \\
\Rightarrow \quad g‘: \vec{x‘}&= \begin{pmatrix} 31 \\ 5 \end{pmatrix} + t \cdot \begin{pmatrix} -9 \\ 13 \end{pmatrix}
\end{align*}
die Gleichung der Bildgeraden $g‘$.
Lass es dir im Lernvideo nochmal erklären, wie man eine Bildgerade bestimmt.
Fixpunkt bestimmen
Bei Fixpunkten handelt es sich um Punkte, die bei einer Abbildung auf sich selbst abgebildet werden, also „fix“ bleiben. Nicht jede mathematische Abbildung hat einen (oder gar mehrere) Fixpunkte. Die Fixpunkte einer Achsenspiegelung sind die Punkte der Spiegelachse. Eine Punktspiegelung hat nur einen Fixpunkt, nämlich deren Zentrum.
Gegeben sei folgende Abbildung, die auf Fixpunkte untersucht werden soll:
\begin{align*}
\vec{x‘} = \begin{pmatrix}
3 & 0 \\ 0 & 3 \end{pmatrix} \cdot \vec{x} + \begin{pmatrix} -6 \\ -8 \end{pmatrix}
\end{align*}
Wenn Fixpunkte existieren, muss folgende Gleichung erfüllt sein:
\begin{align*}
%\begin{pmatrix}
%3 & 0 \\ 0 & 3 \end{pmatrix} \cdot \vec{x} + \begin{pmatrix} -6 \\ -8 \end{pmatrix} &= \vec{x} \notag \\
\begin{pmatrix}
3 & 0 \\ 0 & 3 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} -6 \\ -8 \end{pmatrix} &= \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \notag
\end{align*}
Es ergibt sich ein LGS mit zwei Gleichungen und zwei Unbekannten:
\begin{align*}
3x_1 – 6 &= x_1 \notag \\
3x_2 – 8 &= x_2 \notag
\end{align*}
Es lässt sich eine eindeutige Lösungen finden mit dem Ergebnissen $x_1=3$ und $x_2=4$. Das bedeutet die Abbildung besitzt einen einzigen Punkt, der auf sich selbst abgebildet wird: den Fixpunkt $F(3|4)$.
Was passiert, wenn wenn wir keine eindeutige Lösung für $x_1$ und $x_2$ erhalten?
Wahre Aussage, wie z.B.
\begin{align*}
0=0 \notag \\
3=3 \notag
\end{align*}
bedeutet, dass wir eine Fixpunktgerade vorliegen haben.
Weiteres Vorgehen siehe Abschnitt Fixpunktgerade bestimmen.v
Falsche Aussage, wie z.B.
\begin{align*}
0&=-9 \notag \\
1&=3 \notag
\end{align*}
bedeutet, dass die Abbildung keinen Punkt hat, der auf sich selbst abgebildet wird. Damit sind wir an dieser Stelle fertig!
Lass dir vertiefend von Daniel erklären, wie man einen Fixpunkt bestimmt.
Fixpunktgerade bestimmen
Die Abbildung
\begin{align*}
\alpha :\vec{x‘} = \begin{pmatrix} 2 & -2 \\ -2 & 5 \end{pmatrix} \cdot \vec{x}+ \begin{pmatrix}-1 \\ 2 \end{pmatrix} \notag
\end{align*}
soll auf Fixpunkte untersucht werden. Wenn es einen Fixpunkt geben soll, muss nachstehende Gleichung gelten. Wir erhalten ein Gleichungssystem, welches wir versuchen zu lösen:
\begin{align*}
\begin{pmatrix} 2 & -2 \\ -2 & 5 \end{pmatrix} \cdot \vec{x}+ \begin{pmatrix}-1 \\ 2 \end{pmatrix} &= \vec{x} \notag \\
\begin{pmatrix} 2 & -2 \\ -2 & 5 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}+ \begin{pmatrix}-1 \\ 2 \end{pmatrix} &= \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \quad \textrm{bzw.}\notag \\ \notag \\
\textrm{I} \quad \quad 2x_1 – 2x_2 – 1 &= x_1 \quad |-x_1 \ |+1 \notag \\
\textrm{II} \quad -2x_1 + 5x_2 +2 &= x_2 \quad |-x_2 \ |-1 \notag \\
\textrm{I} \quad \quad \ \ x_1 – 2x_2 &= 1 \notag \\
\textrm{II} \quad -2x_1 + 4x_2 &= -2. \notag
\end{align*}
Wenn wir Gleichung $\textrm{II}+2\cdot \textrm{I}$ rechnen, erhalten wir die Lösung $0=0$! Jetzt bloß keine Panik! Es liegt eine allgemeingültige Aussage vor – was machen wir? Wir sagen, dass z.B. $x_2=t$ gilt und setzen dieses Ergebnis in $\textrm{I}$ ein und erhalten
\begin{align*}
x_1 – 2t &= 1 \notag \\
x_1 &= 1 +2t \notag
\end{align*}
und somit die Fixpunktgerade
\begin{align*}
g: \vec{x}= \begin{pmatrix} 1 + 2 t \\ 0 + 1 t \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ 1 \end{pmatrix}. \notag
\end{align*}
Alle Punkte, die auf dieser Geraden liegen werden auf sich selbst abgebildet. Wer die Gerade lieber in Koordinatenform vorliegen hat, kann sich nach der wahren Aussagen $0=0$ Gleichung $1$ vornehmen und folgendermaßen umschreiben:
\begin{align*}
\textrm{aus} \ 1 : \quad x_1 – x_2 &= 1 \quad \textrm{mit} \ x_1 = x \ \textrm{und} \ x_2 = y \notag \\
x-2y &= 1 \notag \\
\Rightarrow \quad y &= \frac{1}{2}x- \frac{1}{2} \notag
\end{align*}
Fixgeraden bestimmen
Hat eine affine Abbildung einen Fixpunkt (Berechnung sollte klar sein), dann setzt sich eine Fixgerade wie folgt zusammen:
\begin{align*}
g : \vec{x} = \underbrace{\begin{pmatrix} \ \\ \ \end{pmatrix}}_{\textrm{Fixpunkt}} + t \cdot
\underbrace{\begin{pmatrix} \ \\ \ \end{pmatrix}}_{\textrm{Eigenvektor}}
\end{align*}
Wenn also eine Fixgerade existiert, werden Punkte entlang dieser Graden mit dem Richtungsvektor $\vec{u}$ abgebildet, wofür die Berechnung von Eigenwerten und Eigenvektoren notwendig ist.
Einschub Eigenwerte/Eigenvektoren
Ein Eigenvektor einer Abbildung ist in der linearen Algebra ein vom Nullvektor verschiedener Vektor, dessen Richtung durch die Abbildung nicht verändert wird. Ein Eigenvektor wird also nur skaliert und man bezeichnet den Skalierungsfaktor als Eigenwert der Abbildung.
Gegeben sei die Abbildung
\begin{align*}
\alpha : \vec{x‘} = \begin{pmatrix} 1 & 1 \\ 2 & 0 \end{pmatrix} \cdot \vec{x} + \begin{pmatrix} 3 \\ 4 \end{pmatrix}, \notag
\end{align*}
die auf Eigenwerte untersucht werden soll. Dafür ist nur die Matrix wichtig, die bei $\vec{x}$ steht. Der Rest wird nicht betrachtet. Merkt euch: Nehmt diese Matrix und schreibt immer oben links und unten rechts ein $– \lambda$ hin. Wenn wir von dieser Matrix die Determinante bilden und gleich 0 setzen, können wir die Eigenwerte bestimmen. Es gilt
\begin{align*}
det(A-\lambda \cdot E ) &= 0 \notag \\
\Rightarrow \quad det\left( \begin{pmatrix} 1-\lambda & 1 \\ 2 & 0-\lambda \end{pmatrix}\right) &= 0 \notag \\ \notag \\
\Rightarrow \quad (1-\lambda)\cdot (-\lambda) – 2 \cdot 1 &= 0 \notag \\
\lambda^2 – \lambda – 2 &= 0 \quad |\textrm{TR oder PQ-Formel ergbibt} \notag \\
\lambda_1 = -1 \quad &\wedge \quad \lambda_2 = 2, \notag
\end{align*}
wobei $\lambda_1$ und $\lambda_2$ die Eigenwerte sind. Für den Einheitsvektor werden die Eigenwerte einzeln in die Gleichung
\begin{align*}
\begin{pmatrix} 1-\lambda & 1 \\ 2 & 0-\lambda \end{pmatrix} \cdot \begin{pmatrix} u_1 \\ u_2 \end{pmatrix} = \vec{0} \notag
\end{align*}
eingesetzt und nach $u_1$ und $u_2$ aufgelöst. Für $\lambda_1=-1$ folgt das Gleichungssystem:
\begin{align*}
1 \quad 2 u_1 + u_2 &= 0 \notag \\
2 \quad 2 u_1 + u_2 &= 0 \notag
\end{align*}
$1- 2$ ergibt eine wahre Aussage $0=0$. Sei also $u_2=t$, dann folgt für $u_1 = -t/2$, wenn wir $u_2=t$ in $1$ einsetzen. Damit erhalten wir den Eigenvektor
\begin{align*}
\begin{pmatrix} u_1 \\ u_2 \end{pmatrix} = \begin{pmatrix} -\frac{t}{2} \\ t \end{pmatrix} = t \cdot \begin{pmatrix} -\frac{1}{2} \\ 1 \end{pmatrix}. \notag
\end{align*}
Das gleiche machen wir jetzt nochmal für den Eigenwert $\lambda_2=2$ und es folgt analog für den Einheitsvektor
\begin{align*}
\begin{pmatrix} u_1 \\ u_2 \end{pmatrix} = \begin{pmatrix} t \\ t \end{pmatrix} = t \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix}. \notag
\end{align*}
- Sollte es nur einen $\lambda$-Wert geben: Nur ein Eigenwert = Nur ein Eigenvektor!
- Sollte es keinen $\lambda$-Wert geben: Kein Eigenwert = Kein Eigenvektor!
Kommen wir zurück auf die Berechnung einer Fixgerade. Gegeben sei die Abbildung
\begin{align*}
\alpha: \vec{x‘} = \begin{pmatrix} 1 & 0 \\ 0 & 2 \end{pmatrix} \cdot \vec{x} + \begin{pmatrix} 2 \\ 1 \end{pmatrix}, \notag
\end{align*}
von der wir wissen, dass diese keinen Fixpunkt hat – kommt eine falsche Aussage heraus! Das bedeutet jetzt nicht, dass es keine Fixgerade gibt! Wichtig für die Fixgerade sind die Eigenvektoren.
Als Eigenwerte kommen $\lambda_1 = 1$ und $\lambda_2 = 2$ heraus mit den Eigenvektoren
\begin{align*}
\vec{u_1} = t \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} \quad \textrm{und} \quad \vec{u_2} = t \cdot \begin{pmatrix} 0\\ 1 \end{pmatrix}. \notag
\end{align*}
Beide Eigenvektoren werden nun untersucht. Der Ansatz lautet für $\vec{u_1}$:
\begin{align*}
\begin{pmatrix} 1 & 0 \\ 0 & 2 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 2 \\ 1 \end{pmatrix} – \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} &= \mu \cdot \underbrace{\begin{pmatrix} 1 \\ 0 \end{pmatrix}}_{\vec{u_1}} \notag \\
1 \quad x_1 + 2 – x_1 &= \mu \notag \\
2 \quad 2x_2 + 1 – x_2 &= 0 \notag
\end{align*}
Zwei Gleichungen und drei Unbekannte. $x_1$ fällt in $1$ weg und wir erhalten $\mu=2$. Aus $2$ folgt $x_2=-1$. Unsere Fixgerade lautet also für diesen Eigenvektor
\begin{align*}
g: \vec{x} = \begin{pmatrix} x_1 \\ -1 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix}. \notag
\end{align*}
Für den Eigenvektor $\vec{u_2}$ erhalten wir eine falsche Aussage und damit keine weitere Fixgerade.
Weiteres Beispiel: Gegeben sei die Abbildung
\begin{align*}
\alpha : \vec{x‘} = \begin{pmatrix} 0 & 1 \\ 2 & -1 \end{pmatrix} \cdot \vec{x} + \begin{pmatrix} 0 \\ 2 \end{pmatrix}. \notag
\end{align*}
Zudem wissen wir bereits:
- Abbildung besitzt keinen Fixpunkt
- Zwei Eigenwerte mit $\lambda_1 = -2$ und $\lambda_2= 1$
- Zwei Eigenvektoren mit $\vec{u_1}= t \cdot (1,1)^T, \ \vec{u_2}= t \cdot (1,-2)^T$
Für $\vec{u_2}$ gilt:
\begin{align*}
\begin{pmatrix} 0 & 1 \\ 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 0 \\ 2 \end{pmatrix} – \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} &= \mu \cdot \begin{pmatrix} 1 \\ -2 \end{pmatrix} \quad \textrm{bzw. das LGS} \notag \\ \notag \\
\textrm{I} \quad \quad \quad \quad \quad \ x_2 – x_1 &= \mu \notag \\
\textrm{II} \quad 2x_1 – x_2 + 2 -x_2 &= -2 \mu \notag
\end{align*}
Addition von $\textrm{II}+ 2\cdot \textrm{I}$ liefert die falsche Aussage $2=0$! Hier liegt also keine Fixgerade vor.
Für $\vec{u_1}$ gilt:
\begin{align*}
\begin{pmatrix} 0 & 1 \\ 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 0 \\ 2 \end{pmatrix} – \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} &= \mu \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} \quad \textrm{bzw. das LGS} \notag \\ \notag \\
\textrm{I} \quad \quad \quad \quad \quad \ x_2 – x_1 &= \mu \notag \\
\textrm{II} \quad 2x_1 – x_2 + 2 -x_2 &= \mu \notag
\end{align*}
Addition von $\textrm{II}+ 2\cdot \textrm{I}$ liefert $\mu=2/3$! Einsetzen in Gleichung $\textrm{I}$ bringt
\begin{align*}
-x_1 + x_2 &= \frac{2}{3} \quad \textrm{sei} \ x_2 = t \notag \\
-x_1 + t &= \frac{2}{3} \notag \\
x_1 &= t – \frac{2}{3} \notag
\end{align*}
und damit die Fixgerade
\begin{align*}
g: \vec{x} = \begin{pmatrix} 2/3 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix}.\notag
\end{align*}
Verkettung von Abbildungen
Gegeben seien die Abbildungen
\begin{align*}
\alpha : \vec{x‘} &= \begin{pmatrix} 2 & 1 \\ -1 & 3 \end{pmatrix} \cdot \vec{x} \quad \textrm{und} \notag \\
\beta : \vec{x‘} &= \begin{pmatrix} 4 & -5 \\ 1 & 2 \end{pmatrix} \cdot \vec{x}, \notag
\end{align*}
welche verkettet werden sollen. Es gilt
\begin{align*}
\alpha \circ \beta: \quad \vec{x‘} = \left( \begin{pmatrix} 2 & 1 \\ -1 & 3 \end{pmatrix} \cdot \begin{pmatrix} 4 & -5 \\ 1 & 2 \end{pmatrix} \right) \cdot \vec{x} = \begin{pmatrix} 9 & -8 \\ -1 & 11 \end{pmatrix} \cdot \vec{x}. \notag
\end{align*}
Wichtig: Wenn nach der Reihenfolge der Abbildung gefragt wird, gilt hier: Zuerst wird nach $\beta$ und dann nach $\alpha$ abgebildet! Obwohl $\alpha \circ \beta$ etwas anderes vermuten lässt.
Abbildungsgleichung bestimmen
Gegeben sei
\begin{align*}
M = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \quad \textrm{und} \quad \vec{x} = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \notag
\end{align*}
und die Abbildungsvorschrift
\begin{align*}
f(x‘) = M \cdot \vec{x} \quad \textrm{bzw.} \quad \vec{x‘} = M \cdot \vec{x} \quad \textrm{oder} \quad \begin{pmatrix} x_1′ \\ x_2′ \end{pmatrix} = M \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}. \notag
\end{align*}
Es sei bekannt, dass die Punkte $A(1|2)$ und $B(-3|2)$ auf $A'(10|11)$ und $B'(-6|-1)$ abgebildet werden. Die Aufgabe sei es nun, die Matrix $M$ zu bestimmen. Es gilt
\begin{align*}
\textrm{I*} \quad \quad \begin{pmatrix} a & b \\ c & d \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} &= \begin{pmatrix} 10 \\ 11 \end{pmatrix} \notag \\
\textrm{II*} \quad \begin{pmatrix} a & b \\ c & d \end{pmatrix} \cdot \begin{pmatrix} -3 \\ 2 \end{pmatrix} &= \begin{pmatrix} -6 \\ -1 \end{pmatrix}, \notag
\end{align*}
woraus wir ein LGS mit vier Gleichungen und vier Unbekannten erhalten:
\begin{align*}
\textrm{I} \quad \quad \ \ a + 2 b &= 10 \notag \\
\textrm{II} \quad \quad \ \ c + 2 d &= 11 \notag \\
\textrm{III}\quad -3a + 2 b &= -6 \notag \\
\textrm{IV} \quad -3c + 2 d &= -1 \notag
\end{align*}
Auflösung des Gleichungssystem bringt für die gesuchte Matrix $M$ die Abbildungsgleichung
\begin{align*}
\vec{x‘} = \underbrace{\begin{pmatrix} 4 & 3 \\3 & 4 \end{pmatrix}}_{M} \cdot \vec{x}. \notag
\end{align*}
Lass es dir nochmal von Daniel zeigen, wie man eine Abbildungsgleichung bestimmt.

