Wärme, Arbeit und Energie
Das Verständnis von Wärme, Arbeit und Energie wird für das Verstehen des ersten Hauptsatzes der Thermodynamik vorausgesetzt. In diesem Artikel lernt ihr all diese Themen kennen. Wir erklären euch Schritt für Schritt, begleitend durch Lernvideos, wie Wärme, Arbeit und Energie definiert werden.
Inhaltsverzeichnis
- Energiearten
- Wärme und Arbeit
- Egoistische Vorzeichenregel
- Volumenänderungsanteil verschiedener Zustandsänderungen
- Technische Arbeit
19,99€
Energiearten
Für den ersten Hauptsatz nehmen wir wieder die Kolbenpumpe aus dem Beispiel des Abschnitts „0. Hauptsatz“ zur Hand. Zunächst ist es sinnvoll, zu überlegen, welche Formen von Energie in dieser Pumpe vorliegen können.
Die innere Energie $u$ basiert auf der Wärmeenergie, die auf einem bestimmten Temperaturniveau vorliegt und die wir durch die kalorische Zustandsgleichung beschreiben können.
Halten wir die Kolbenpumpe aus dem Fenster und lassen sie fallen, fällt sie herunter und knallt auf den Boden. Dieser wenig überraschende Umstand offenbart zwei weitere Energieformen, die ein System wie die Kolbenpumpe aufweisen kann.
Die potentielle Energie: Bewegen wir ein System aus einem stabilen Zustand (zum Beispiel auf dem Boden stehend) gegen die Erdbeschleunigung nach oben, steigt die potentielle Energie in diesem System. Sie nimmt proportional mit der geodätischen Höhe $z$ (dem Abstand zum stabilen Zustand, also bspw. der Erdoberfläche) zu
$$E_{pot} = m \cdot g \cdot z$$
Die kinetische Energie: Aus der Bewegung einer Masse resultiert eine Energie, die sich bei einer Änderung der Geschwindigkeit dieser Masse (etwa durch einen Stoß) übertragen kann. Die kinetische Energie berechnet sich mit
$$E_{kin} = \frac{1}{2} \cdot m \cdot v^2$$
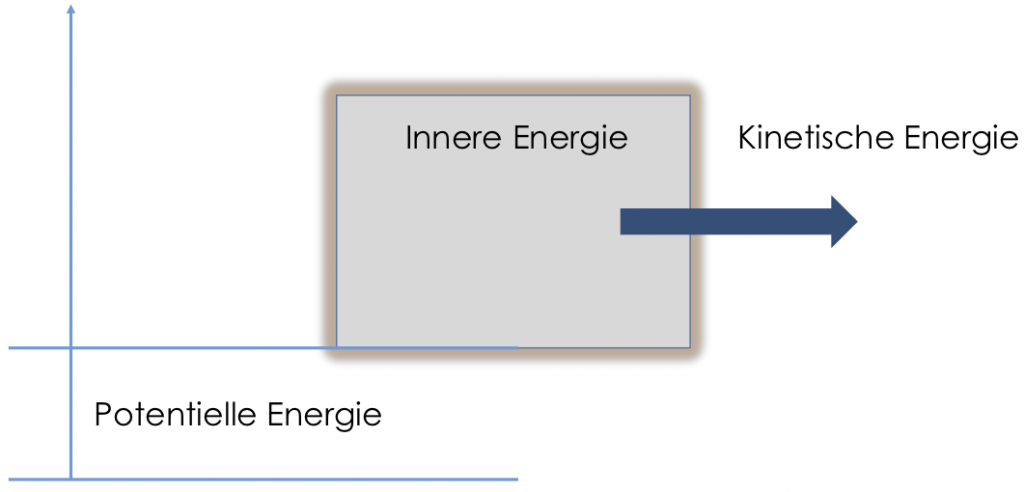
Die Kolbenpumpe beinhaltet also innere Energie und kann zusätzlich kinetische und potentielle Energie innehaben. Wodurch können sich diese Energien ändern?
Wärme und Arbeit
Die Wärme als Energieform, die bei einem bestimmten Temperaturniveau vorliegt, ist uns bereits in „Nochmal die Temperatur“ begegnet. Wärme ist die Energiemenge, die in einem System vorliegen kann. Sie ist aber auch eine Prozessgröße. Wir können Wärme einem System hinzuführen (Wasser auf dem Herd erwärmen) oder entnehmen (warmes Bier in das Eisfach legen).
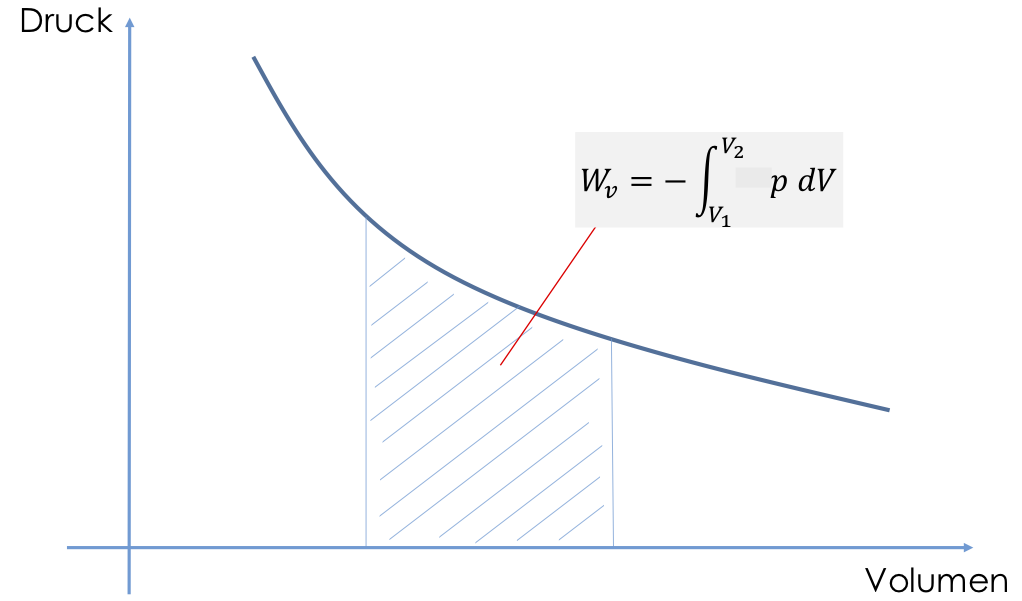
Arbeit ist ein neuer Begriff. Wir verstehen darunter eine Kraft, die an einem System einen bestimmten Weg entlang verrichtet wird, um den Zustand des Systems zu ändern. Wenn ich meinen Reifen aufpumpe, muss ich dafür zunächst den Kolben meiner Kolbenpumpe nach unten drücken. Ich verrichte Arbeit. Arbeit an einem geschlossenen System nennen wir Volumenänderungsarbeit, weil wir durch die ausgeübte Kraft entlang eines bestimmen Weges das Volumen des Systems ändern können. Die Volumenänderungsarbeit ist wie folgt definiert
Volumenänderungsarbeit $W_V = – \displaystyle\int p \ \text{d}V$
Wieso aber ist die Volumenänderungsarbeit negativ definiert?
19,99€
Egoistische Vorzeichenregel
Die Kolbenpumpe hat ein Volumen $V_1$ und wird auf ein Volumen $V_2 < V_1$ komprimiert. Wir gehen davon aus, dass diese Kompression isobar stattfindet. Die durch den Kolben verdrängte Luft kann also entweichen. Dann können wir den Druck als Konstante aus dem Integral ziehen und erhalten
$$W_{V,12} = – p \displaystyle\int_{V_1}^{V_2} \ \text{d}V = \underbrace{-p \cdot \underbrace{(V_2 – V_1)}_{<0}}_{>0}$$
Es gilt ja $V_2 < V_1$, weshalb der Klammerausdruck kleiner als 0 ist. Durch das negative Vorzeichen wird der Ausdruck insgesamt aber positiv.
Egoistische Vorzeichenregel: Wärme oder Arbeit, die einem System zugeführt werden, sind stets größer als Null. Wärme und Arbeit, die einem System entzogen werden, sind kleiner als Null.
Volumenänderungsanteil verschiedener Zustandsänderungen
Für isobare Zustandsänderungen haben wir die Gleichung zur Berechnung der Volumenänderungsarbeit berechnet:
$$W_{V,12} = – p \cdot (V_2 – V_1)$$
Wollen wir diese Gleichung spezifisch darstellen, müssen wir sie durch die Masse m des Systems teilen.
$$w_{v,12} = – p \cdot (v_2 – v_1)$$
Wir werden alle Gleichungen in spezifischer Form herleiten. Wer die andere Darstellung bevorzugt, kann die Gleichungen einfach mit der Masse multiplizieren.
Für die übrigen Zustandsänderungen müssen wir ein bisschen mehr rechnen, weil der Druck nicht einfach als Konstante vor das Integral gezogen werden kann. Schauen wir uns isotherme Zustandsänderungen an. Es sei darauf hingewiesen, dass wir die Zustandsänderungen idealer Gase betrachten.
Die Gleichung zur Berechnung der Volumenänderungsarbeit in spezifischer Form lautet
$$w_{v} = – \displaystyle\int p \ \text{d}v$$
Den Druck müssen wir über die Temperatur umformulieren, um nach dem Volumen integrieren zu können. Da wir nach dem spezifischen Volumen integrieren, nutzen wir das ideale Gasgesetz formuliert nach dem Druck
$$p = \frac{R\cdot T}{v} $$
und erhalten durch Einsetzen in das Integral
$$W_{V} = -R \cdot T \displaystyle\int_{v_1}^{v_2} \frac{1}{v} \ \text{d}v = -R \cdot T \cdot \ln \left( \frac{v_2}{v_1} \right) = R \cdot T \cdot \ln \left( \frac{p_2}{p_1} \right)$$
als Gleichung zur Berechnung der Volumenänderungsarbeit bei isothermen Zustandsänderungen.
Isochore Zustandsänderungen werden bei konstantem Volumen durchgeführt. Die Volumenänderungsarbeit ist dabei konsequenterweise Null.
Für polytrope und reversibel adiabate Zustandsänderungen ist die Herleitung ein bisschen aufwendiger, da zusätzlich die kalorische Zustandsgleichung verwendet werden muss. Die zugehörigen Gleichungen finden sich im Anhang und werden am Ende des Abschnitts in Videos ausführlich erläutert.
Technische Arbeit
Ohne uns dessen bewusst zu sein, haben wir bisher geschlossene Systeme (wie die Kolbenpumpe) betrachtet. Geschlossene Systeme zeichnen sich dadurch aus, dass sie keinen Stoffaustausch mit ihrer Umgebung durchführen können.
In der Thermodynamik haben wir es manchmal mit Kreislaufprozessen zu tun. Diese Kreislaufprozesse bewegen Massenströme $\dot{m}_i$ durch ein System, die Zustandsänderungen durchlaufen. Die Zustandsänderungen in einem Abschnitt des Systems finden also in offenen (Teil-)systemen ab, denen ein Massenstrom $\dot{m}_i$ permanent zu und abgeführt wird.
Solche offenen Systeme haben kein definiertes Volumen $V$, das sich durch eine Volumenänderungsarbeit verändern ließe. Trotzdem kann in einem Kreislaufprozess Arbeit verrichtet werden, die als technische Arbeit bezeichnet wird.
$$w_t = \displaystyle\int v \ \text{d}p$$
Die technische Arbeit wird spezifisch, also pro Masse dargestellt. Wird in einem Kreislaufsystem isochor der Druck verändert, wird hierfür die folgende technische Arbeit benötigt
$$w_t = \displaystyle\int_{p_1}^{p_2} v \ \text{d}p = v \cdot (p_2-p_1)$$
Für isotherme Zustandsänderungen in offenen System ist das Vorgehen analog zur Volumenänderungsarbeit. Das spezifische Volumen wird anhand des idealen Gasgesetzes durch einen Ausdruck der (konstanten) Temperatur ersetzt.
$$w_t = \displaystyle\int_{p_1}^{p_2} v \ \text{d}p = R \cdot T \cdot \displaystyle\int_{p_1}^{p_2} \frac{1}{p}\ \text{d}p = R \cdot T \cdot \ln\left(\frac{p_2}{p_1}\right)$$
Für isobare Zustandsänderungen kann keine technische Arbeit berechnet werden. Der Ausdruck $\text{d}p$ im Integral ist bei isobaren Zustandsänderungen analog zur Volumenänderungsarbeit bei isochoren Zustandsänderungen null. Die technische Arbeit polytroper und reversibler Zustandsänderungen wird in den Videos am Ende des Abschnittes ausführlich hergeleitet und findet sich als Gleichung zusammengefasst im Anhang.
Wir kennen nun also Energieformen geschlossener Systeme und können für jede Zustandsänderung Arbeit an ihnen verrichten. Es wird Zeit, diese neuen Erkenntnisse an einem Beispiel zu vertiefen.
Bevor wir uns dem schon ersten Hauptsatz zuwenden, müssen wir Wärme als Prozessgröße verstehen.
Wärme in geschlossenen und offenen Systemen
Wärme ist wie Arbeit eine Prozessgröße, die Systemen zu- oder abgeführt werden kann. Es ist sinnvoll, Wärme Zu- und Abfuhren berechnen zu können. Wir kennen bereits die isochore und isobare Wärmekapazität aus der Beschäftigung mit der kalorischen Zustandsgleichung.
Spezifische Wärmekapazität: Menge an Wärme, die zu- oder abgeführt werden muss, um ein $\si{kg}$ eines Stoffes um ein Kelvin zu erwärmen oder abzukühlen.
Für isobare Zustandsänderungen muss die isobare Wärmekapazität mit der zu erzielenden Temperaturänderungen multipliziert werden:
$$q_{12,p} = c_p \cdot (T_2-T_1)$$
Wir haben Glück: die Gleichung deckt sich mit der egoistischen Vorzeichenregel: Führen wir Wärme ab, ist $T_2$ kleiner als $T_1$, die Differenz wird negativ und somit ist die abgeführte Wärme kleiner als Null.
Die isochore Wärmezufuhr berechnet sich dann mit
$$q_{12,v} = c_v \cdot (T_2-T_1)$$
Diese Gleichungen gelten jeweils sowohl für offene als auch geschlossene Systeme.
Isotherme Wärmezufuhren sind etwas, auf das wir uns gedanklich einlassen müssen. Führen wir Wärme zu oder ab, ändert sich dadurch die Temperatur. Soll für eine isotherme Wärmezufuhr die Temperatur aber gleich bleiben, müssen wir den Energiemangel oder -überschuss durch die Zu- oder Abfuhr von Arbeit kompensieren. Erwärmen wir Luft in einer Pumpe, steigt die Temperatur der Luft. Es entsteht eine isotherme Zustandsänderung, in die durch die Erwärmung expandiere Luft als Volumenänderungsarbeit genutzt wird.
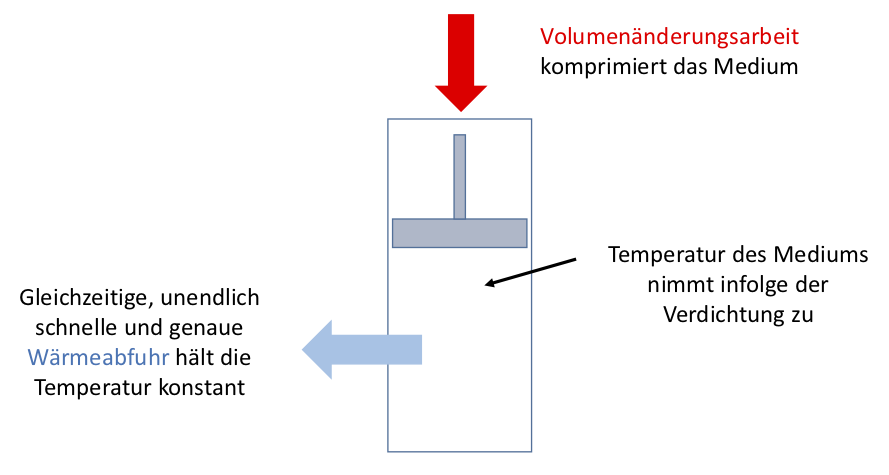
Isotherme Zustandsänderung
Diese Vorstellung ist idealtypisch, weil sie die Zeitabhängigkeit von Wärmeübertragung vernachlässigt. Physikalisch muss der Betrag der zugeführten Wärmemenge für eine isotherme Zustandsänderung gleich der abgeführten Arbeit sein (oder anders herum). Es gilt deshalb für ein geschlossenes System
$$q_{T,12} = -R\cdot T \cdot \ln \left( \frac{v_2}{v_1} \right)$$
und für ein offenes System
$$q_{T,12} = -R\cdot T \cdot \ln \left( \frac{p_2}{p_1} \right)$$
Bei reversibel adiabaten Zustandsänderungen wird keine Wärme zu- oder abgeführt. Deshalb sind sie ja adiabat. Infolgedessen können für diese Zustandsänderungen auch keine Wärmemengen berechnet werden.
Für polytrope Zustandsänderung ist die Gleichung zur Berechnung der Wärme im Anhang angegeben.
In den folgenden Videos erfahrt im mehr über Wärme und Arbeit…
isothermen Zustandsänderung (geschl. System)
reversibel adiabaten Zustandsänderung (geschl. System)
offenes System:
polytrope Zustandsänderung: