
Die Kalorische Zustandsgleichung
Die thermische Zustandsgleichung des idealen Gases liefert uns Informationen über die Zustandsgrößen Druck, spezifisches Volumen und Temperatur. Wir kennen aus dem ersten Kapitel bereits die innere Energie (Formelzeichen $u$), die wir noch nicht berechnen können. Das ideale Gasgesetz wird deshalb um die kalorische Zustandsgleichung des idealen Gases ergänzt.
Inhaltsangabe
- Grundlagen – Die Freiheitsgrade
- Grundlagen – Wärmekapazitäten
- Grundlagen – Zusammenhang der Stoffdaten idealer Gase
- Grundlagen – Wärmekapazitäten
- Kalorische Zustandsgleichung
19,99€
Atome und Moleküle können Energie speichern, die wir als Wärme eines Stoffes wahrnehmen. Diese Wärmeenergie ist abhängig von der Temperatur eines Stoffes, wobei unterschiedliche Stoffe bei gleicher Temperatur unterschiedlich viel Wärme speichern können. Der Grund hierfür ist die molekulare Struktur eines Stoffes. Wir brauchen also ein Modell, dass die Wärme eines Stoffes in Abhängigkeit seiner Temperatur und molekularen Struktur beschreibt. Wir stellen uns vor, dass ein Molekül Energie in Form von Translation, Rotation und Schwingung speichern kann. Wie viel Energie gespeichert werden kann, hängt von der Anzahl der Freiheitsgrade ab, die das Molekül (oder Atom) aufweist.
Grundlagen Kalorische Zustandsgleichung – Die Freiheitsgrade
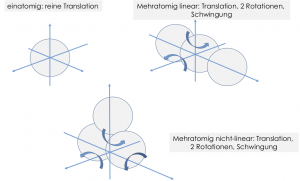
Ein einatomiges Gas besitzt drei translatorische Freiheitsgrade in alle Raumrichtungen. Rotatorische Freiheitsgrade werden berücksichtigt, wenn sich das „Aussehen“ des Atoms oder Moleküls durch die Rotation ändert. In unserer Vorstellung der Atome als Punktmassen ist dies für ein einatomiges Molekül nicht der Fall. Es besitzt als keine rotatorischen Freiheitsgrade. Schwingungsfreiheitsgrade entstehen durch die Schwingung der Atome eines Moleküls untereinander. Für einatomige Moleküle liegen keine Schwingungsfreiheitsgrade vor.
Zweiatomige oder mehratomige Linearmoleküle wie Kohlenstoffdioxid besitzen mehr Freiheitsgrade. Sie können sich um zwei Achsen so drehen, dass sich ihr „Aussehen“ ändert und die einzelnen Atome können zueinander schwingen.
Bei der Schwingung des Atoms eines Moleküls gegen die anderen Atome liegen potentielle und kinetische Energie vor. Ein Schwingungsmodus wird dabei als die Fähigkeit eines Atoms bezeichnet, gegen ein anderes Atom zu schwingen. Pro Schwingungsmodus liegen aufgrund der potentiellen und kinetischen Energie der Atome zwei Schwingungsfreiheitsgrade vor. Dieser Ansatz wird als Gleichverteilungssatz bezeichnet. Wir legen fest:
- ein zweiatomiges Gas besitzt einen Schwingungsmodus, also zwei Schwingungsfreiheitsgrade
- ein dreiatomiges lineares Gas besitzt vier Schwingungsmodi (jedes Atom mit jedem anderen und das mittlere gegen die beiden äußeren), also acht Schwingungsfreiheitsgrade
- ein dreiatomiges nichtlineares Gas besitzt drei Schwingungsmodi (jedes Atom mit jedem anderen)
Für komplexere Moleküle verliert der Gleichverteilungssatz seine Aussagekraft, da er dort nur für sehr hohe Temperaturen gilt. Der hier vorgestellte Ansatz gibt die maximal möglichen Schwingungsfreiheitsgrade an. Tatsächlich sind nicht immer alle Schwingungsmodi angeregt, weshalb in Klausuraufgaben oft explizit vorgegeben wird, mit wie vielen Schwingungsmodi oder -freiheitsgraden zu rechnen ist.
Grundlagen Kalorische Zustandsgleichung – Wärmekapazitäten
Wie können wir die Vorstellung der Speicherung von Energie auf molekularer Ebene nutzen? Wir können beobachten, dass unterschiedliche Stoffe bei gleicher Temperatur unterschiedliche Mengen an Wärme speichern und wissen nun, dass dies in ihrer Molekülstruktur begründet liegt. Wir brauchen also eine stoffspezifische Größe, die beschreibt, wie viel Wärme pro Masse und Erwärmung um ein Kelvin in einem Stoff gespeichert werden kann. Diese Größe ist die sogenannte Wärmekapazität.
Stoffe können bei Temperaturerhöhungen infolge isochorer und isobarer Zustandsänderungen (isotherm würde keinen Sinn ergeben) unterschiedliche Mengen an Wärme speichern. Wir definieren deshalb eine isochore und isobare Wärmekapazität idealer Gase. Die isochore Wärmekapazität $c_v$ kann anhand der oben besprochenen Freiheitsgrade des Moleküls und der spezifischen Gaskonstante berechnet werden.
Beispiel 3
$CO_2$ ist ein lineares dreiatomiges Molekül. Es besitzt folglich drei translatorische und zwei rotatorische Freiheitsgrade. Es liegen vier Schwingungsmodi vor, von denen zwei angeregt sind. Wir rechnen also mit vier Schwingungsfreiheitsgraden. Die spezifische Gaskonstante berechnet sich mit
$$R_{CO_2} = \frac{R_m}{M_{CO_2}} = \frac{8314 \frac{\text{J}}{\text{molK}}}{43{,}99 \cdot \frac{10^{-3} \text{kg}}{\text{mol}}} = 188{,}99 \frac{\text{J}}{\text{kgK}}$$
und damit folgt für die isochore Wärmekapazität von Kohlenstoffdioxid
$$c_{v,CO_2} = \frac{R_m}{M_{CO_2}} = \frac{8314 \frac{\text{J}}{\text{molK}}}{43{,}99 \cdot \frac{10^{-3} \text{kg}}{\text{mol}}} = 188{,}99 \frac{\text{J}}{\text{kgK}}$$
Dieser Wert gilt übrigens für $CO_2$ bei etwa $270°\text{C}$ und Umgebungsdruck.
Grundlagen Kalorische Zustandsgleichung – Zusammenhang der Stoffdaten idealer Gase
Wir können für ein ideales Gas die isochore Wärmekapazität berechnen. Für die isobare Wärmekapazität gilt
$$c_p = c_v + R$$
Die Wärmemenge bei einer isobaren Zustandsänderung muss größer sein als bei einer isochoren Zustandsänderung des gleichen Temperaturintervalls. Die isobare Wärmekapazität ist betragsmäßig größer, es kann also pro kg bei einer Temperaturerhöhung um ein Kelvin mehr Wärme gespeichert werden.
Der Isentropenexponent $\kappa$ zur Berechnung reversibel adiabater Zustandsänderungen wird durch den Quotienten der Wärmekapazitäten berechnet
$$\kappa = \frac{c_p}{c_v}$$
Kalorische Zustandsgleichung
Das Ziel dieses Abschnitts ist eine Gleichung, mit der wir die innere Energie eines Stoffes als Funktion seiner Molekülstruktur und seiner Temperatur berechnen können. Diese Gleichung definieren wir als die kalorische Zustandsgleichung idealer Gase
$$u_2 = u_1 + c_v \cdot (T_2 – T_1)$$
Leider ist diese Gleichung ungenau. Wir haben oben gesehen, dass die Wärmekapazität keine konstante Stoffgröße ist, sondern sich anhand der angeregten Schwingungsmodi mit der Temperatur verändert. Die Wärmekapazität ist also eine Funktion der Temperatur, wodurch sich der Ansatz oben komplexer darstellen lässt. Für Klausuraufgaben wird in der Regel ein Wert vorgegeben oder muss anhand der Gleichungen oben berechnet werden. Der dadurch gemachte Fehler bei der Berechnung der inneren Energie wird toleriert.
Die kalorische Zustandsgleichung unter Verwendung einer konstanten Wärmekapazität ermöglicht uns, Wärme Zu- und Abfuhren zu berechnen.
Ausblick: welche Zustandsgleichungen hier NICHT beschrieben werden
Die Beschäftigung mit der thermischen und kalorischen Zustandsgleichung idealer Gase zeigt, dass diesen Modellen Grenzen gesetzt sind. Komplexe Moleküle, Stoffverhalten bei hohen Drücken und Dichten und nicht-gasförmige Stoffe können nicht beschrieben werden. An dieser Stelle werden einige Modellansätze genannt, die bei Interesse in der Fachliteratur vertieft werden können.
Das ideale Gasgesetz geht von ausdehnungslosen Massepunkten als Teilchen aus. Die Berücksichtigung des Volumens von Teilchen findet sich etwa in kubischen Zustandsgleichungen (van der Waals, 1873 oder Redlich-Kwong, 1949).
Das Verhalten realer Fluide unterliegt Phasenänderungen. Die Gleichung nach Clausius-Clapeyron kann genutzt werden, um den Übergang zwischen den Phasen eines Stoffes zu berechnen.
Die Virialform der Zustandsgleichung erweitert das ideale Gasgesetz, aufgelöst nach dem Realgasfaktor, um einen polynomialen Ansatz. Diese Erweiterung soll den Realgasfaktor jenseits der Gültigkeit des idealen Gasgesetzes modellieren, um Zustandsänderungen berechnen zu können.
Moderne Ansätze versuchen, das Verhalten realer Fluide in allen Phasen ganzheitlich korrekt zu beschreiben. Der Rechenaufwand zur numerischen Lösung der entsprechenden sogenannten Fundamentalgleichungen ist je nach Stoff hoch, sodass die Stoffmodellierung bis heute Aufgabe der thermodynamischen Forschung ist.
19,99€

