
Grundrechenarten
Die Grundrechenarten sind das Fundament der Mathematik. Wir unterscheiden grundsätzlich vier Grundrechenarten, die wir euch auf dieser Seite erklären werden. Macht euch mit den Begrifflichkeiten vertraut, da diese im weiteren Verlauf immer wieder auftauchen und erwähnt werden.
Auf dieser Seite erklären wir diese Grundrechenarten:
- Übersicht der Grundrechenarten
- Zahlenmengen
- Rechengesetze
- Vielfache und Teiler
- Teilbarkeitsregeln
- Runden
- Einheiten
Übersicht zu den Grundrechenarten der Mathematik
Addition : $$ \underbrace{2}_{Summand}+\underbrace{4}_{Summand}=\underbrace{6}_{Summe}$$
Subtraktion : $$ \underbrace{7}_{Minuend}-\underbrace{3}_{Subtrahend}=\underbrace{4}_{Differenz}$$
Multiplikation : $$ \underbrace{2}_{Faktor}\bullet \underbrace{3}_{Faktor}=\underbrace{6}_{Produkt}$$
Division : $$ \underbrace{4}_{Dividend}:\underbrace{2}_{Divisor}=\underbrace{2}_{Quotient}$$
Wir haben für dich eine Playlist zum Thema Grundrechenarten zusammengetellt
Zahlenmengen
Nachfolgend findet ihr neben den Grundrechenarten eine Übersicht der wichtigsten Zahlenmengen.
Natürliche Zahlen
$ \mathbb{N}=\left\{0,\ 1,\ 2,\ 3,\ 4,\ 5\right.\left.\dots \right\}\to $ Natürliche Zahlen sind ganze, positive Zahlen.
Ganze Zahlen
$ \mathbb{Z}=\left\{\dots -2,\ -1,\ 0,\ 1,\ 2\right.\left.\dots \right\}\to$ Ganze Zahlen sind sowohl ganze positive als auch ganze negative Zahlen mit der Null.
Rationale Zahlen
$ \mathbb{Q}=\left\{\dots -1,\ \dots ,\ -\frac{1}{2},\ \dots ,\ \right.-\frac{1}{3},\ \dots ,\ 0,\ \left.\dots ,\ \frac{1}{3},\ \dots ,\ \frac{1}{2},\dots ,\ 1,\ \dots \right\}\to $ Rationale Zahlen sind Zahlen, die sich als Bruch darstellen lassen; ganze Zahlen lassen sich auch als Bruch darstellen.
Reelle Zahlen
$ \mathbb{R}=\left\{\dots ,\ \pi ,\ \dots ,\ \sqrt{2},\ \ \right.\left.\ \dots \right\}\ \to $ Reelle Zahlen sind alle Zahlen.
Rechengesetze
Grundsätzlich gilt immer Punkt- vor Strichrechnung und Potenzieren vor Punktrechnung. Außerdem werden Ausdrücke in Klammern immer zuerst berechnet.
Des Weiteren gelten die folgenden Rechengesetze:
Kommutativgesetz (Vertauschungsgesetz; gilt nur für die Addition und die Multiplikation, nicht für die Subtraktion und Division)
Allgemein: $ a+b=b+a \quad $
Beispiel: $ 7+2=2+7 $
Allgemein: $ a\cdot b=b\cdot a \quad $
Beispiel: $ 2\cdot 7=7\cdot 2 $
Assoziativgesetz (Vereinigungsgesetz; gilt ebenfalls nur für die Addition und die Multiplikation, nicht für die Subtraktion und Division)
Allgemein: $ \left(a+b\right)+c=a+(b+c)$
Beispiel: $\left(7+2\right)+3=7+(2+3)$
Allgemein: $\left(a\cdot b\right)\cdot c=a\cdot (b\cdot c)$
Beispiel: $\left(7\cdot 2\right)\cdot 3=7\cdot (2\cdot 3)$
Distributivgesetz (Verteilungsgesetz)
Allgemein: $\left(a+b\right)\cdot c=a\cdot c+b\cdot c$
Beispiel: $\left(2+3\right)\cdot 7=2\cdot 7+3\cdot 7$
Vielfache und Teiler (kgV und ggT)
Vielfache und Teiler sind euch wahrscheinlich das letzte Mal in der fünften Klasse vorgesetzt worden. Sie spielen aber eine wichtige Rolle und sollten auf keinen Fall vernachlässigt werden. Das Thema Bruchrechnung wird euch wesentlich leichter fallen, wenn ihr mit den Begriffen in diesem Kapitel sicher umgehen könnt.
Vielfache
- $3,\ 6,\ 9,\ 12\dots $ sind Vielfache von $3$: $V_3=\left\{3,\ 6,\ 9,\ 12\right.\left.\dots \right\}$ ist die Vielfachenmenge von $3$
- Die gemeinsamen Vielfachen von 2 und 3 sind die Zahlen, die sowohl zu $V_2=\left\{2,\ 4,\ 6,\ 8,\ 10\right.\left.\dots \right\}$ als auch zu $V_3=\left\{3,\ 6,\ 9,\ 12,\ 15\right.\left.\dots \right\}$ gehören. Das kleinste gemeinsame Vielfache (kgV) von 2 und 3 ist demnach 6.
Teiler
- $1,\ 2,\ 4,\ 5,\ 10,\ 20$ sind die ganzzahligen, positiven Teiler von $20$: $T_{20}=\left\{1,\ 2,\ 4,\ 5,\ 10,\ 20\right\}$ ist die Teilermenge von 20.
- Die gemeinsamen Teiler von 10 und 20 sind die Zahlen, die sowohl zu $T_{10}=\left\{1,\ 2,\ 5,\ 10\right\}$ als auch zu $T_{20}=\left\{1,\ 2,\ 4,\ 5,\ 10,\ 20\right\}$
gehören. Der größte gemeinsame Teiler (ggT) von 10 und 20 ist demnach 10.
Teilbarkeitsregeln
- Eine Zahl ist genau dann durch 2 teilbar, wenn ihre Endziffer eine gerade Zahl ist.
Beispiel: $0,\ 2,\ 4,\ 6,\ 8 \ \dots$
- Eine Zahl ist genau dann durch 3 teilbar, wenn ihre Quersumme durch 3 teilbar ist.
Beispiel: Die Quersumme von 744 ist $7+4+4=15$. $15$ ist durch $3$ teilbar, also ist $744$ auch durch $3$ teilbar.
- Eine Zahl ist genau dann durch 4 teilbar, wenn ihre letzten beiden Ziffern eine durch 4 teilbare Zahl bilden.
Beispiel: 2524; 24 ist durch 4 teilbar, also ist auch 2524 durch 4 teilbar.
- Eine Zahl ist genau dann durch 5 teilbar, wenn ihre Endziffer eine 0 oder 5 ist.
Beispiel: 1255 oder 9870; da die Endziffer eine 5 oder 0 aufweist, sind 1255 und 9870 durch 5 teilbar.
- Eine Zahl ist genau dann durch 6 teilbar, wenn sie sowohl durch 2 als auch durch 3 teilbar ist.
Beispiel: 24 ist sowohl durch 2 als auch durch 3 teilbar, also ist sie auch durch 6 teilbar.
- Eine Zahl ist genau dann durch 8 teilbar, wenn ihre letzten drei Ziffern eine durch 8 teilbare Zahl bilden.
Beispiel: 42976; 976 ist durch 8 teilbar, also ist auch 42976 durch 8 teilbar.
- Eine Zahl ist genau dann durch 9 teilbar, wenn ihre Quersumme durch 9 teilbar ist.
Beispiel: Die Quersumme von 999 ist $9+9+9=27$. Da 27 durch 9 teilbar ist, ist also auch 999 durch 9 teilbar.
Runden
Beim Runden von Zahlen gelten die beiden folgenden Regeln:
- Die Ziffer nach der Rundungsstelle ist eine 0, 1, 2, 3 oder 4 $\rightarrow$ abrunden
- Die Ziffer nach der Rundungsstelle ist eine oder 5, 6, 7 oder 8 $\rightarrow$ aufrunden
Beispiel:
Die Zahl 5356 soll auf Hunderter gerundet werden. Zu diesem Zweck stellen wir die Zahl in einer Stellenwerttafel dar:

Die Stelle rechts von unserer Rundungsstelle (Hunderter) ist die Zehnerstelle. Dort finden wir eine 5, also wird aufgerundet. Aus unserer Zahl 5356 wird jetzt 5400.
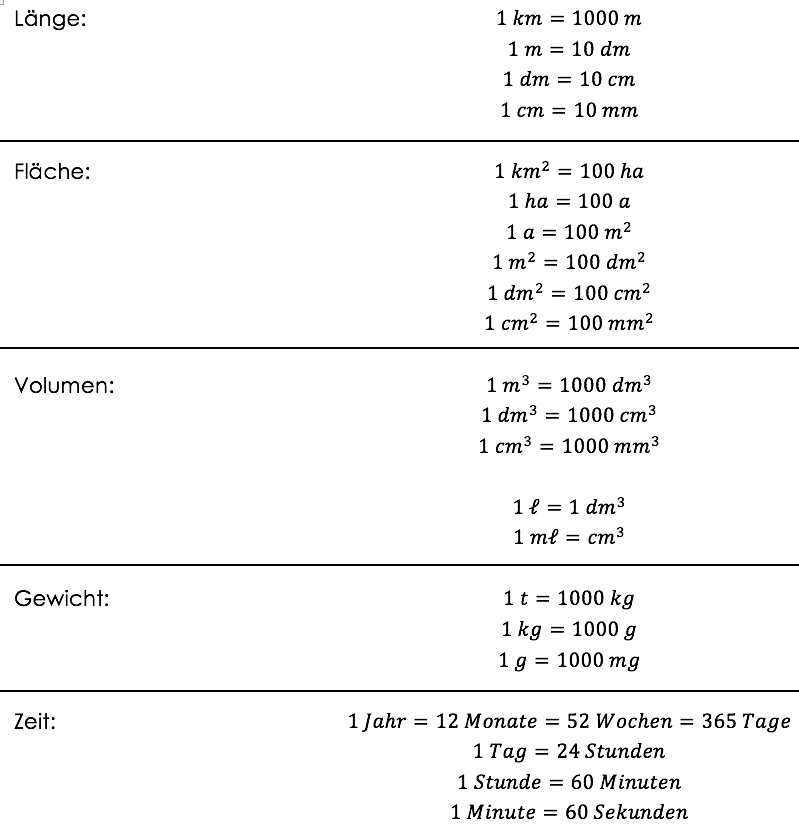
Einheiten
- Bei der Umrechnung in die nächstkleinere Einheit wird multipliziert.
- Bei der Umrechnung in die nächstgrößere Einheit wird dividiert.
Die folgende Darstellung zeigt die wichtigsten Umrechnungen:
Beispielaufgabe zum Thema Einheitenrechnung
Wie hoch ist die durchschnittliche Lebenserwartung eines Mannes ungefähr?
a) 6700 Stunden
b) 67000 Stunden
c) 670000 Stunden
Lösung:
Ein Mann erreicht ein ungefähres Alter von 78 Jahren. Das entspricht 78∙365=28740 Tagen. Das wiederrum sind 28740∙24=683280 Stunden. 670000 Stunden müssen angekreuzt werden.
Bei solchen Aufgaben geht es nicht darum, das genaue Ergebnis herauszufinden. Deswegen steht auch in der Frage das Wort „ungefähr“. Hier gibt es eine Spannweite von Lösungen, welche akzeptiert werden. Man hätte hier auch mit einem durchschnittlichen Alter von 75 oder 80 Jahren anfangen können.
NEU
