
Quadratische Funktionen
Du steckst beim Lernen fest und brauchst Hilfe beim Thema „Quadratische Funktionen“? In diesem Artikel erklären wir dir alles zu folgenden Themen:
- Was sind quadratische Funktionen?
- Nullstellen einer Parabel
- Allgemeine Form und Scheitelpunktform
- Allgemeine Form in Scheitelpunktform
- Scheitelpunktform in die allgemeine Form
Schaut euch zu Beginn das Einführungsvideo zu Parabeln und quadratischen Funktionen von Daniel an!
Was sind quadratische Funktionen?
Der Graph von quadratischen Funktionen ist immer eine Parabel. Zu Beginn wollen wir uns einmal die sogenannte Normalparabel $f\left(x\right)=x^2$ angucken:
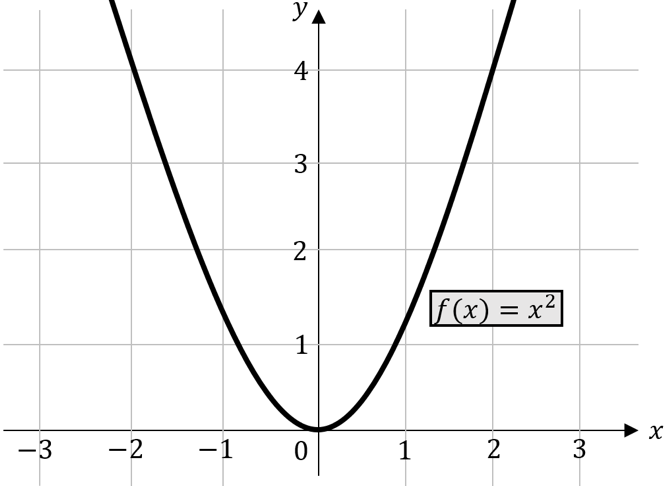
Wir sehen, dass unsere Normalparabel ihren Scheitelpunkt im Punkt $(0|0)$ hat. Der Scheitelpunkt ist der tiefste oder höchste Punkt einer Parabel. Diese Normalparabel können wir auf verschiedene Arten und Weisen transformieren (verändern oder manipulieren). Das bedeutet, dass wir:
- ihren Scheitelpunkt in $x$-Richtung verschieben können (nach links oder nach rechts) oder
- in $y$-Richtung verschieben (nach oben oder nach unten)
- Außerdem können wir sie strecken (schmaler machen) oder stauchen (breiter machen) oder
- wir können sie an der $x$-Achse spiegeln, so dass ihre Öffnung nach unten zeigt.
Verschiebung in $x$-Richtung
Die Verschiebung in $x$-Richtung können wir in unserer Funktionsgleichung wie folgt berücksichtigen. Dazu werfen wir einen Blick auf das nachfolgende Koordinatensystem.
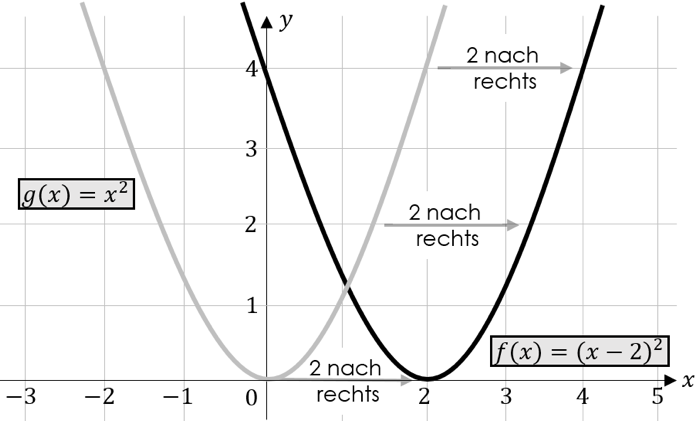
Der Scheitelpunkt dieser Parabel und alle anderen Punkte wurden ausgehend von der Normalparabel (hier: $g\left(x\right)=x^2$) um $2$ Einheiten nach rechts verschoben.
Wenn wir einen Blick auf die Funktionsgleichung werfen, sehen wir, dass sie wie folgt lautet:
\[f\left(x\right)={(x-2)}^2\]
Eine Verschiebung in $x$-Richtung kann man immer daran erkennen, dass der Wert, um welchen die Parabel verschoben wurde, mit umgekehrten Vorzeichen in der Klammer auftaucht.
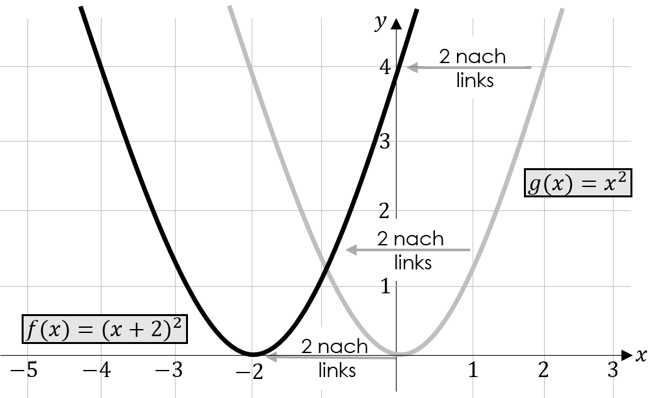
Dazu wollen wir uns ebenfalls eine Parabel angucken, welche nach links verschoben wurde. Die Funktionsgleichung dieser Parabel lautet:
\[f\left(x\right)={(x+2)}^2\]
Die Parabel wurde um $2$ Einheiten nach links verschoben. Das erkennen wir daran, dass die $-2$ in unserer Gleichung innerhalb der Klammer mit einem umgekehrten Vorzeichen auftaucht.
NEU
Verschiebung in $y$-Richtung
Die Verschiebung in $y$-Richtung erkennt ihr daran, dass der Wert, um den die Parabel in $y$-Richtung verschoben wurde ohne Klammer mit dem korrekten Vorzeichen angehängt wird.
Betrachten wir die untenstehende Parabel. Diese Parabel wurde um $2$ Einheiten nach oben verschoben.
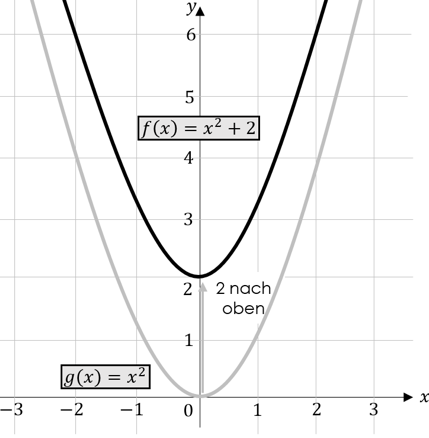
Die zugehörige Funktionsgleichung muss also $f\left(x\right)=x^2+2$ lauten.
Als nächstes wollen wir eine Parabel angucken, welche nach unten verschoben wurde.
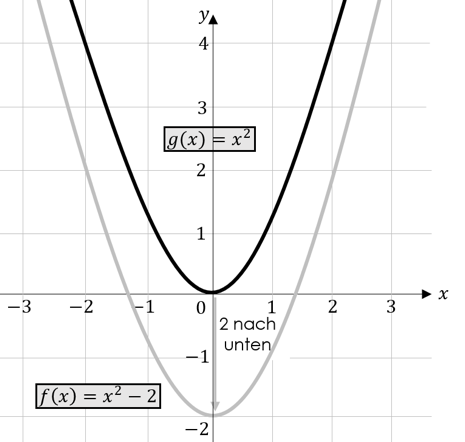
Wir erkennen wieder an unserer Funktionsgleichung $f\left(x\right)=x^2-2$, dass unsere Parabel nach unten verschoben wurde.
Natürlich ist es auch möglich, sowohl eine Verschiebung in $x$-Richtung als auch eine Verschiebung in $y$-Richtung gleichzeitig durchzuführen. Dazu betrachten wir die folgende Parabel.
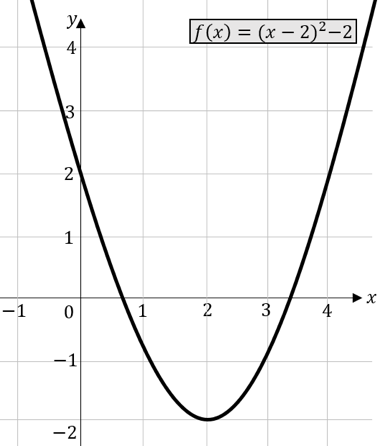
Diese Parabel wurde um $2$ Einheiten nach rechts und um $2$ Einheiten nach unten verschoben. Die Funktionsgleichung lautet: $f\left(x\right)={(x-2)}^2-2$
In der Klammer erkennen wir die Verschiebung um $2$ Einheiten nach rechts und hinter der Klammer erkennen wir die Verschiebung um $2$ Einheiten nach unten. Eine Funktionsgleichung, welche in der obigen Form vorliegt, wird Scheitelpunktform genannt, da es direkt möglich ist die Koordinaten des Scheitelpunktes abzulesen. In unserem Fall also $S(2|-2)$.
Streckung/Stauchung
Wenn wir eine Parabel strecken oder stauchen wollen, müssen wir die Funktionen mit einem Faktor $a$ multiplizieren.
Aus $f\left(x\right)=x^2$ wird dann $f\left(x\right)=a\cdot x^2$. Dabei gelten die folgenden Regeln:
- $1<a$: Streckung
- $0<a<1$: Stauchung
Der Faktor $a$ gibt also an, ob es sich um eine Streckung oder um eine Stauchung handelt. Der Faktor $a$ befindet sich entweder direkt vor dem $x^2$ oder, falls unsere Funktionsgleichung in der Scheitelpunktform vorliegen sollte, direkt vor der Klammer. Dazu wollen wir uns den folgenden Sachverhalt kurz vor Augen halten.
Die Normalparabel $f\left(x\right)=x^2$ hat den Faktor $a=1$. Diesen schreiben wir aus Gründen der mathematischen Faulheit aber nicht hin. Die Normalparabel ist also weder gestreckt noch gestaucht.
Ebenso ist unsere Parabel mit der Funktionsgleichung $f\left(x\right)={(x-2)}^2-2$ weder gestreckt noch gestaucht, da der Faktor $a$ direkt vor der Klammer ebenfalls den Wert $a=1$ hat.
Eine gestreckte Parabel könnte die folgende Gleichung haben:
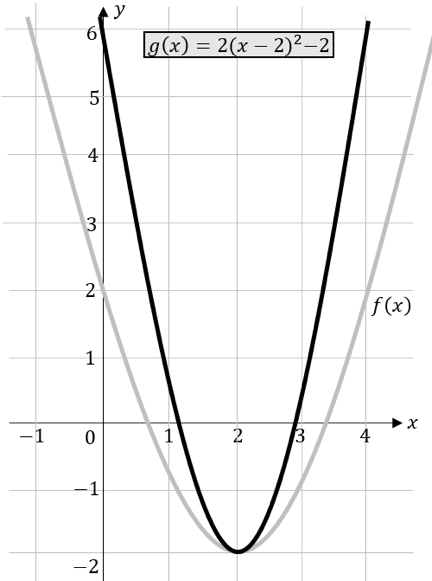
\[g\left(x\right)=2{(x-2)}^2-2\]
Wir erkennen, dass für unseren Faktor $a$ jetzt $a=2$ gilt. Da $a$ größer als 1 ist, müsste die Parabel gestreckt werden. Dazu betrachten wir die die Funktionen $f(x)={\left(x-2\right)}^2-2$ und $g(x)$ in der nebenstehenden Abbildung. Wir sehen, dass unsere Parabel $g$ im Verhältnis zur Parabel $f$ wesentlich schmaler aussieht. Sie ist also gestreckt.
Im Gegensatz dazu wollen wir uns auch eine gestauchte Parabel angucken. Wir betrachten die nachfolgende Darstellung.
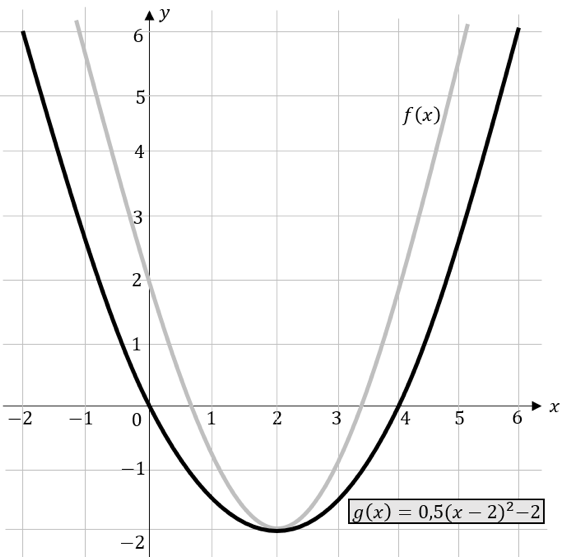
Die Funktionsgleichungen unserer beiden Parabeln lauten:
\[f\left(x\right)={(x-2)}^2-2\] und \[g\left(x\right)=0,5{(x-2)}^2-2\]
Wir sehen, dass unsere Parabel $g$ breiter ist als unsere Parabel $f$. Sie ist also gestaucht.
Spiegelung an der $x$-Achse
Wir erkennen eine an der $x$-Achse gespiegelte (nach unten geöffnete) Parabel daran, dass der Faktor $a$ negativ ist. Dazu betrachten wir die folgende Darstellung: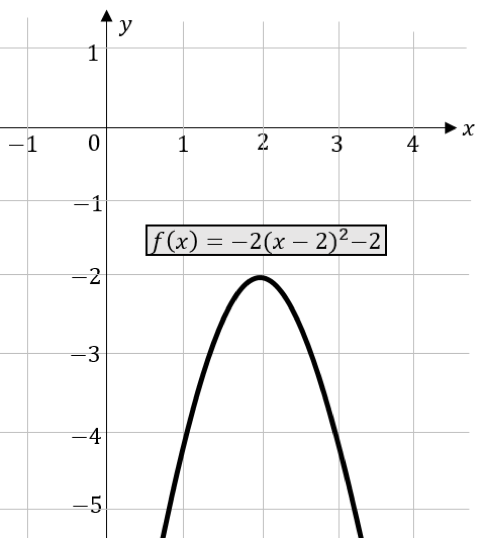
Die Funktionsgleichung unserer Parabel lautet $f\left(x\right)=-2{\left(x-2\right)}^2-2$. Der Faktor $a$ hat den Wert $a=-2$, er ist also negativ. Insgesamt wurden an dieser Parabel also die folgenden Transformationen durchgeführt:
- Verschiebung um 2 Einheiten nach rechts
- Verschiebung um 2 Einheiten nach unten
- Streckung mit dem Faktor $a=2$
- Spiegelung an der $x$-Achse (Öffnung zeigt nach unten)
NEU
Nullstellen einer Parabel
Die Nullstellen (Schnittpunkte mit der -Achse) kann man mit den in den vorherigen Kapiteln angesprochenen Verfahren herausfinden. Welches Verfahren am ehesten geeignet ist, hängt natürlich davon ab, in welcher Form die Funktionsgleichung angegeben ist. Macht euch an dieser Stelle bitte klar, dass eine Parabel entweder zwei Nullstellen, eine oder eventuell sogar keine Nullstelle besitzt.
Daniel erklärt euch die Nullstellen einer Parabel nochmal im Lernvideo.
Allgemeine Form und Scheitelpunktform
Die Funktionsgleichungen von Parabeln können in zwei verschiedenen Formen vorliegen:
Allgemeine Form: $f\left(x\right)=a\cdot x^2+b\cdot x+c$
Scheitelpunktform: $f\left(x\right)=a\cdot {\left(x-d\right)}^2+e$
Man kann die allgemeine Form in die Scheitelpunktform und die Scheitelpunktform in die allgemeine Form überführen.
Schau dir das Lernvideo zum Thema Scheitepunkt erkennen an!
Allgemeine Form in Scheitelpunktform
Wir gehen davon aus, dass wir die folgende Funktionsgleichung vorliegen haben. Im ersten Schritt klammern wir den Faktor $a$ vor dem $x^2$ (hier also die 2) aus und erhalten:
\[f\left(x\right)=2x^2+4x-3=2(x^2+2x-1,5)\]
Als nächstes wenden wir die erste binomische Formel auf die ersten drei Summanden an und erhalten:
\[f\left(x\right)=2[{\left(x+1\right)}^2-2,5]\]
Jetzt multiplizieren wir noch den Faktor $a$ mit der konstanten Zahl am Ende der Funktionsgleichung:
\[f\left(x\right)=2{(x+1)}^2-5\]
Jetzt können wir erneut die Koordinaten unseres Scheitelpunkts ablesen: $S\ (-1|-5)$.
Scheitelpunktform in die allgemeine Form umwandeln
Wir gehen davon aus, dass wir die folgende Funktionsgleichung vorliegen haben:
\[f\left(x\right)=3{(x-2)}^2+5\]
Als erstes wenden wir die zweite binomische Formel an um die Klammer aufzulösen. Denkt daran, dass der Term, der durch die Anwendung der binomischen Formel entsteht, in Klammern gesetzt werden muss.
\[f\left(x\right)=3\left(x^2-4x+4\right)+5\]
Anschließend wird der Klammerausdruck mit dem Faktor $a$ (hier 3) multipliziert.
\[f\left(x\right)=3x^2-12x+12+5\]
Zum Schluss fassen wir zusammen und erhalten unsere Funktionsgleichung in allgemeiner Form:
\[f\left(x\right)=3x^2-12x+17\]
Beispielaufgabe Quadratische Funktionen
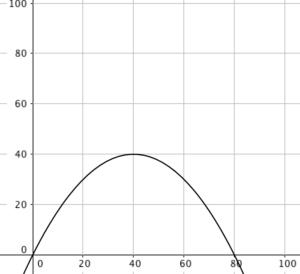
Der unten abgebildete Graph der Funktion $f(x)=-0,025x^2+2x$ beschreibt die Flugbahn eines Golfballs nach dem Abschlag. Die -Achse gibt die horizontale Entfernung vom Abschlagspunkt an, die -Achse die Höhe des Golfballs.
- Welche maximale Höhe erreicht der Golfball auf seiner Flugbahn?
- In welcher Höhe befindet sich der Golfball bei einer horizontalen Entfernung von 20m?
- Wie weit ist der Landepunkt des Golfballs vom Abschlagspunkt entfernt?
Lösung:
Aufgabenteil 1:
Die maximale Höhe lässt sich bei nach unten geöffneten Parabeln direkt an der y-Koordinate des Scheitelpunkts erkennen. Der Scheitelpunkt unserer Parabel hat die Koordinaten $S(40|40)$. Die maximale Höhe unseres Golfballs beträgt demnach $40$.
Aufgabenteil 2:
Im ersten Aufgabenteil wurde bereits beschrieben, dass die jeweiligen ?-Koordinaten die Höhe des Golfballs angeben. Wir suchen jetzt nach der Höhe über der $20$-Markierung. Diese lässt sich nicht genau direkt am Graphen der Funktion ablesen. Deswegen benötigen wir nun unsere Funktionsvorschrift und setzen den Wert $20$ ein. Wir erhalten:
\begin{align*}
f(20)=−0,025 \cdot 20^2+2 \cdot 20=30
\end{align*}
Der Golfball erreicht eine Höhe von $30$ Metern ab der $20$-Markierung.
Aufgabenteil 3:
Der Landepunkt des Golfballs wird durch die rechte Nullstelle unseres Graphen dargestellt. Diese kann man hier problemlos ablesen. Unsere rechte Nullstelle hat die Koordinaten $N_2(80|0)$. Die Entfernung zum Abschlagspunkt beträgt also genau $80$.
An dieser Stelle werden wir auf einen alternativen Lösungsweg eingehen, falls man durch die Aufgabenstellung gezwungen ist, diese rechnerisch bestimmen zu müssen. Zunächst setzen wir unsere Funktionsvorschrift gleich 0 und erhalten:
\begin{align*}
−0,025x^2+2x=0
\end{align*}
Diese Gleichung lösen wir nun nach $x$ auf, indem wir zunächst ein $x$ ausklammern:
\begin{align*}
x \cdot (−0,025x+2)=0
\end{align*}
Jetzt können wir den Satz vom Nullprodukt anwenden und erhalten:
\begin{align*}
x=0 \vee −0,025x+2=0
\end{align*}
Wir erhalten also sofort unsere linke Nullstelle, nämlich an der Stelle $0$ im Ursprung. Unsere rechte Nullstelle erhalten wir, indem wir die übriggebliebene Gleichung nach $x$ auflösen:
\begin{align*}
\begin{array}{rrcll}
& −0,025 \cdot x + 2 & =& 0 &|- 2 \\
\Leftrightarrow & −0,025 \cdot x & =& -2 & |:(−0,025) \\
\Leftrightarrow & x & =&80 & \end{array}
\end{align*}
Wir erhalten unser erwartetes Ergebnis und haben damit gezeigt, dass der Landepunkt 80 Meter entfernt vom Abschlagspunkt liegt.
Daniel zeigt dir, wie du die Scheitelpunktform in die allgemeine Form bringst.
Hier Merkzettel zum Thema Quadratische Funktionen herunterladen!
