
Die Hardy-Weinberg-Gleichung
Mithilfe der Hardy-Weinberg-Gleichung kann die Allelhäufigkeit einer Population (mit zwei verschiedenen Allelen für ein Gen) in den folgenden Generationen berechnet werden.
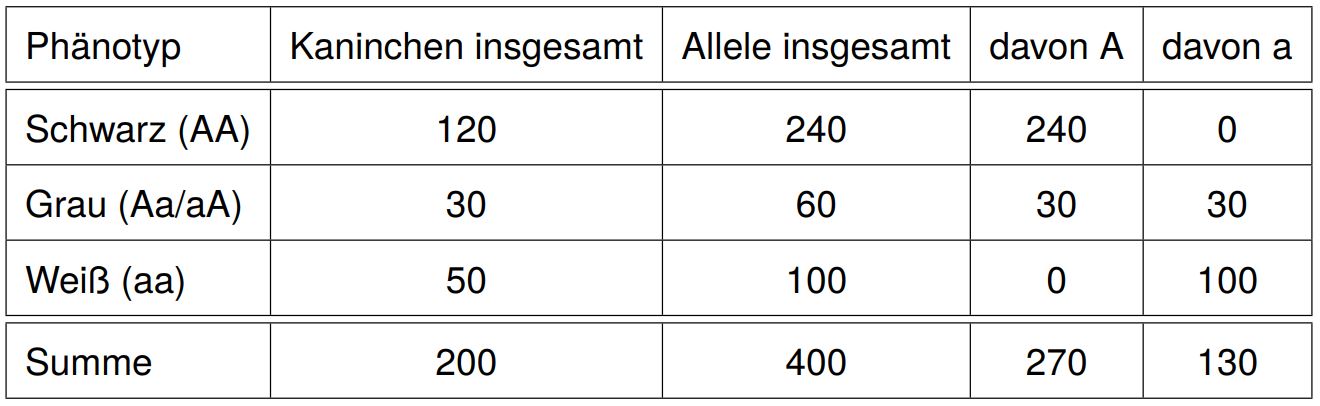
Beispielhaft wird die Hardy-Weinberg-Gleichung hier anhand einer Kaninchenpopulation erläutert, in der für das Gen „Fellfarbe“ die Allele Schwarz (dominant, A) und Weiß (rezessiv, a) vorkommen. Heterozygote Träger der Allele, also Individuen mit dem Genotypen Aa, haben graues Fell. In unserer Beispielpopulation gibt es insgesamt 200 Individuen. 120 davon sind schwarz (AA), 50 sind weiß (aa) und 30 sind grau (Aa/aA). Anhand dieser Angaben kann man nun auszählen, wie viele dominante (A) und wie viele rezessive (a) Allele in der Population vorhanden sind
14,99€
Nun müssen die relativen Häufigkeiten von beiden Allelen zu der Gesamtheit der Allele berechnet werden. Dazu teilt man die Allelhäufigkeit A bzw. a durch alle Allele:
\begin{align*}
\textbf{Allel A:} \quad \frac{270}{400} \ = \ {0,675} \text{(= 67, 5%)} \quad \textbf{bzw. Allel a:} \quad \frac{130}{400} \ = \ {0,325} \text{(= 32, 5%)}
\end{align*}
Jetzt kommt die Gleichung ins Spiel, mit der die Häufigkeiten der Allele für die nächste Generation berechnet werden kann:
\begin{align*}
p^2 \ + \ 2pq \ + \ q^2 \ = \ 1
\end{align*}
mit p als relative Häufigkeit (in %) des Allels A im Genpool, q als relative Häufigkeit (in %) des Allels a im Genpool und 1 als Gesamtheit der Population, also 100%.
Diese Formel in Wörter übersetzt: homozygot (AA) + heterozygot (Aa/aA) + homozygot (aa) = 1
Möchte man nun die Häufigkeiten der verschiedenen Allele in der nächsten Generation berechnen, so muss man für alle drei möglichen Genotypen (AA, Aa, aa) die Wahrscheinlichkeiten berechnen. Dies tut man, indem man die oben berechneten relativen Häufigkeiten in die Formel einsetzt. Heraus kommt eine Prozentangabe dazu, wie viele Kaninchen der nächsten Generation mit diesem Genotypen existieren.
\begin{align*}
\begin{array}{llll}
\text{Genotyp AA:} \quad & p^2 = p \cdot p = 0{,}675 \cdot 0{,}675 \approx 0{,}455 & \ (\approx 45{,}5\%)
\\
\text{Genotyp aa:}\quad & q^2 = q \cdot q = 0{,}325 \cdot 0{,}325 \approx 0{,}105 &\ (\approx 10{,}5\%)
\\
\text{Genotyp Aa/aA:}\quad & 2 pq = 2 \cdot 0,675 \cdot 0{,}325 \approx 0{,}438 &\ (\approx 43{,}8\%)
\end{array}
\end{align*}
Das Hardy-Weinberg-Gesetz lässt sich nur bei idealen Populationen anwenden. Diese zeichnen sich durch Folgendes aus:
- es gibt keine Mutationen
- es gibt keine Migration zwischen verschiedenen Populationen
- es gibt keine Zufallseffekte
- es herrscht Panmixie (jeder paart sich mit jedem)
- kein Genotyp hat Selektionsnachteile.
Man bemerkt schnell, dass diese Merkmale in der freien Natur nicht vorkommen. Daher ist die Anwendung des Hardy-Weinberg-Gesetzes lediglich auf theoretische Überlegungen limitiert und kann für reale, natürliche Populationen nicht eins zu eins übernommen werden.
14,99€

