Die Redoxreihe

Um die Redoxreihe zu erklären schauen wir uns zunächst ein interessantes Phänomen an: Wenn wir in eine Kupfersulfat-Lösung ein Zinkblech halten, bildet sich an dem Zinkblech eine elementare Kupferschicht. Halten wir aber in eine Zinksulfat-Lösung ein Kupferblech, bildet sich keine elementare Zinkschicht. Wir können sogar vorhersagen, wann eine solche Reaktion funktioniert und wann nicht. Dafür brauchen wir die elektrochemische Spannungsreihe (auch Redoxreihe genannt).

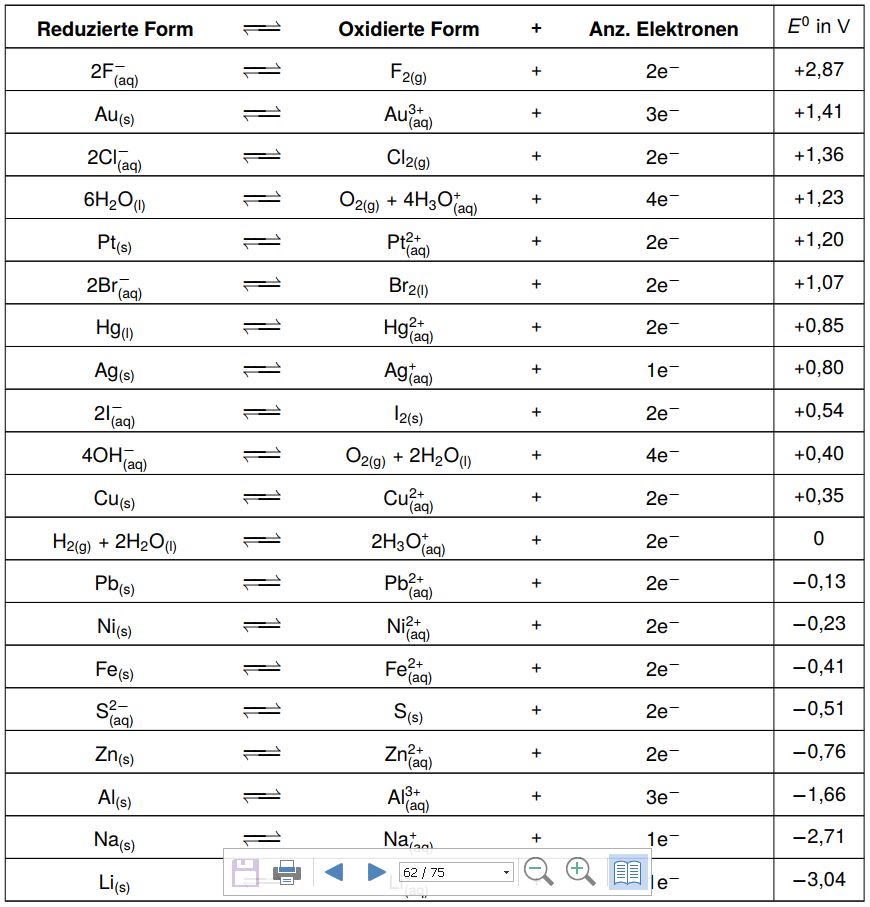
Schauen wir uns diese elektrochemische Spannungsreihe etwas genauer an. Wir haben immer ein korrespondierendes Redoxpaar und die entsprechend beteiligte Elektronenzahl gegeben.

Betrachten wir Kupfer: Die reduzierte Form in der Tabelle ist Cu, das elementare Kupfer. Die oxidierte Form ist Cu2+. Um diese beiden ineinander zu überzuführen, müssen zwei Elektronen abgegeben bzw. aufgenommen werden. Jetzt steht in der letzten Spalte die Zahl +0,35. Dieser Wert ist das sogenannte Standardpotenzial E0. Im Folgenden haben wir einen ganz bestimmten Versuchsaufbau, mit dessen Hilfe das Standardpotenzial bestimmt wird:

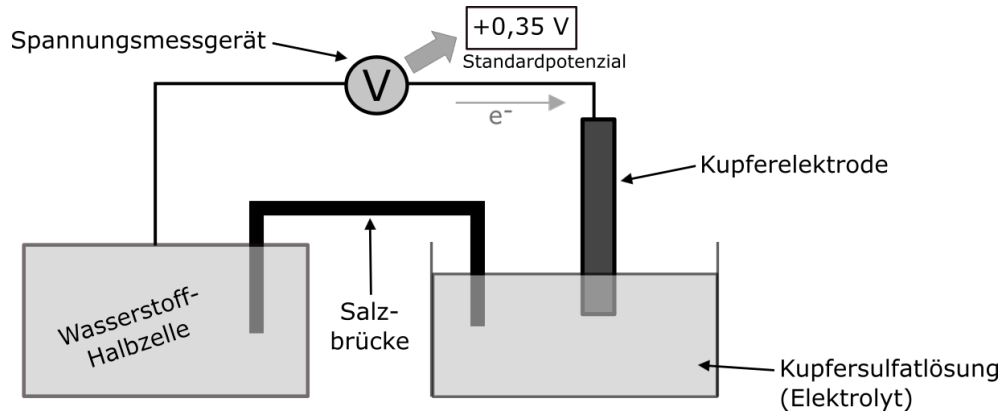
Wir tauchen eine Kupferelektrode in eine Kupfersulfat-Lösung, sodass sich eine Kupferhalbzelle bildet. Die Kupferelektrode verbinden wir über einen Draht mit einer Wasserstoffhalbzelle. Das ist im Prinzip genau das Gleiche wie die Kupferhalbzelle, mit dem Unterschied, dass sie ein bisschen anders aufgebaut werden muss, da Wasserstoff, anders als Kupfer, gasförmig ist.

Die beiden Halbzellen verbinden wir nun mit einer Salzbrücke. Wenn wir nun noch einen Spannungsmesser anschließen, können wir beobachten, dass eine Spannung von +0,35 V anliegt. Das ist genau der Wert, der dann auch in der elektrochemischen Spannungsreihe steht. Jetzt kommen in der Spannungsreihe auch negative Standardpotenziale vor. Das Vorzeichen des Standardpotenzials gibt an, in welche Richtung die Elektronen fließen. Bei der Kupferhalbzelle haben wir ein positives Standardpotenzial, das heißt, die Elektronen fließen zur Kupferhalbzelle hin.

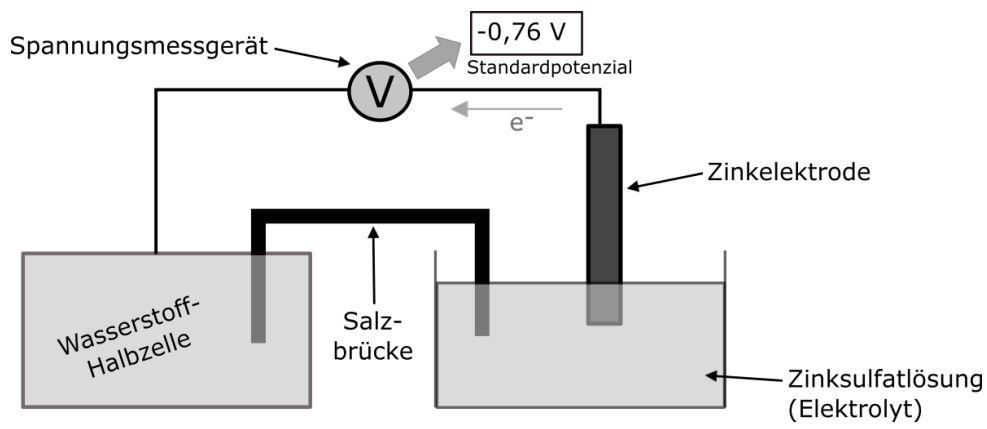
Bei einer Zinkhalbzelle können wir ein Standardpotenzial von −0,76 V beobachten. In diesem Fall fließen die Elektronen von der Zinkhalbzelle weg. Wir sagen auch, dass Zink ein unedles Metall ist, weil es seine Elektronen gerne abgibt. Kupfer hingegen ist ein edles Metall, da es seine Elektronen nicht gerne abgibt und daher eher in der elementaren Form vorliegt.

Bei der elektrochemischen Spannungsreihe ist zu beachten, dass die Werte für das Standardpotenzial für 1 molare Lösung gelten. Bei anderen Konzentrationen ändern sich die Werte ebenfalls.

Jetzt wissen wir, was die Werte in der Tabelle bedeuten. Wozu benötigen wir diese?

Schauen wir uns nochmals das anfängliche Beispiel mit dem Zinkblech in Kupfersulfat-Lösung und dem Kupferblech in Zinksulfat-Lösung an. Mit der Redoxreihe können wir voraussagen, bei welcher Variante die Ionen aus der Lösung zu dem elementaren Metall reagieren und bei welcher Variante nicht.

Schauen wir uns dazu Kupfer und Zink in der Redoxreihe an.

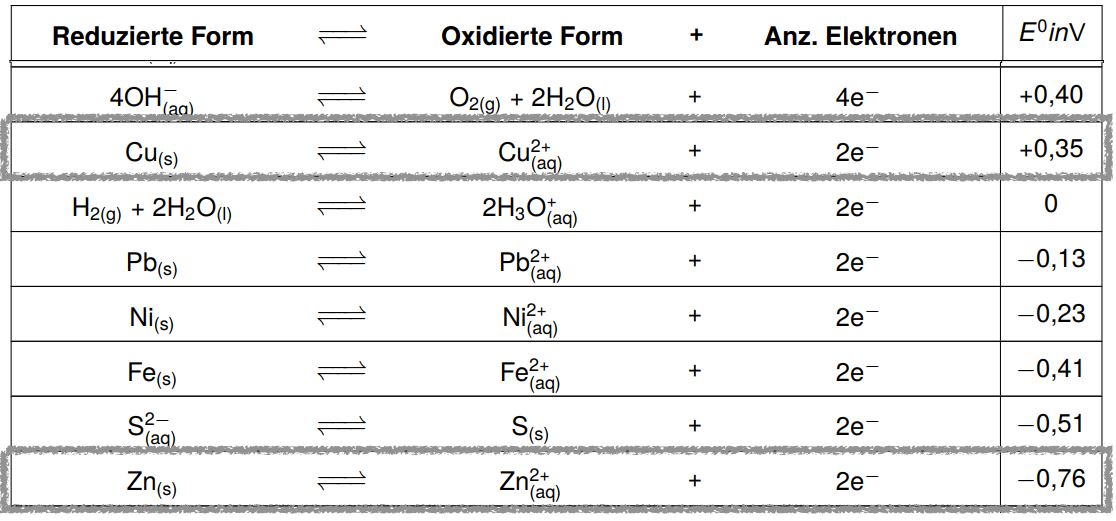
Kupfer steht in der Tabelle höher Zink. Das bedeutet, dass die Reaktion zum elementaren Kupfer hin eher stattfindet als die zum elementaren Zink, da Zink seine Elektronen gerne abgibt, Kupfer aber nicht.

Im Allgemeinen können wir also sagen, dass die Reaktion stattfindet, wenn ein edleres Metall entsteht und dass sie nicht stattfindet, wenn ein unedleres entstehen würde.

Die Werte der Standardpotenziale werden dann also innerhalb der Tabelle nicht kleiner, sondern größer. Dann gilt die Regel natürlich genau umgekehrt!

Wenn wir nun zwei verschiedene Halbzellen, z.B. eine Kupfer- und eine Zinkhalbzelle, zusammenschließen, können wir mithilfe der elektrochemischen Spannungsreihe auch berechnen, wie hoch die Spannung ist, die damit erzeugt werden kann. Dazu ziehen wir den kleineren Wert vom größeren ab:

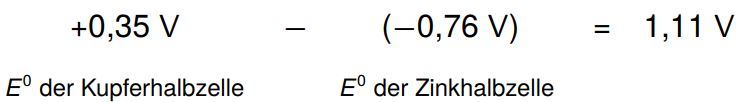
Die 1,11 V entsprechen jetzt der maximalen Spannung, die durch diese galvanische Zelle geliefert werden kann bzw. der minimalen Spannung, die angelegt werden muss, um die Reaktion wieder umzukehren.