
Grundlagen
Wichtige Grundlagen
Vorzeichen:
+ und –
Ganze Zahlen:
2, 3, 4, ..
Brüche:
$\frac{3}{4}, \frac{7}{10}$
Buchstaben:
$a,b,x,…$
Kombination:
$-3x+4a$, $\frac{3}{4}x-2,5$…l>
Potenzen:
- $a \cdot a \cdot a = a^3, x \cdot x \cdot x \cdot x = x^4$
- Merke: $a+a+a=3a$
- Merke: $x^3+x^4$ kann man nicht weiter zusammenfassen!
Klammern ausmultiplizieren:
$2\cdot(x-3)=2x-6$
$(x-4)^2=x^2-8x+16$ oder $(x-4)(x-4)=x^2-4x-4x+16=x^2-8x+16$
Binomische Formeln
1. $(a+b)^2=a^2+2ab+b^2$
2. $(a-b)^2=a^2-2ab+b^2$
3. $(a+b)\cdot (a-b)=a^2-b^2$
Neu!
Potenzen und Potenzgesetze
Erfahrungen besagen, dass ca. 50 % aller Versagensfälle von Klausuren oft auf mangelnde Kenntnisse der Potenzgesetze zurückzuführend sind. Dieses Thema ist also außerordentlich wichtig, da wir mit Hilfe dieser Kenntnisse verschiedenste Ausdrücke umschreiben und gegebenenfalls vereinfachen können.
Ausgangspunkt:
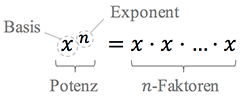
beschreibt die $n$-te Potenz von $x$.
Im Folgenden sollen die drei fundamentalen Potenzgesetze vorgestellt werden.
\begin{align*}
x^m \cdot x^n = x^{m+n}\\
x^n \cdot y^n = (xy)^n\\
(x^n)^m = x^{n \cdot m}
\end{align*}
Zusätzlich sind diese Regeln zum Umschreiben von Potenzen und Wurzeln hilfreich:
\begin{align*}
& x^{-n}= \frac{1}{x^n}, \ \ \ \ \ \ \ \ \ \ x^{\frac{1}{m}} = \sqrt[m]{x}, \\ \\
& x^{\frac{n}{m}} = \sqrt[m]{x^n},\ \ \ \ \ \ \ \ \ \ \frac{x^m}{x^n}=x^{m-n}, \\ \\
& \frac{x^p}{y^p}= \left( \frac{x}{y} \right)^p, \ \ \ \ \ \ \ \ \ \ x^0 =1, \\ \\
& \sqrt[n]{x} \cdot \sqrt[n]{y} = \sqrt[n]{xy}, \ \ \ \ \ \ \ \ \ \ \sqrt[m]{\sqrt[n]{x}} = \sqrt[m\cdot n]{x}
\end{align*}
Diese Zusammenhänge müsst ihr nicht auswendig können, aber ihr solltet sie aus den drei Potenzgesetzen ableiten können.
Hier noch weitere Beispiele zum Umschreiben, die euch das Leben in der Klausur erleichtern werden:
\begin{align*}
&\frac{1}{x} = x^{-1}, \ \ \ \ \ \ \ \frac{1}{x^{2}} = x^{-2},\\ \\
&\frac{1}{x{^3}} = x^{-3} \frac{4}{x^{5}} = 4x^{-5}, \ \ \ \ \ \ \ \frac{7}{3x^{3}} = \frac{7}{3}x^{-3} \\ \\
&\frac{70}{3x^{10}} = \frac{70}{3} x^{-10}, \ \ \ \ \ \ \ \sqrt[3]{x} = x^{\frac{1}{3}} \\ \\
&\sqrt{x} = x^{\frac{1}{2}} = \sqrt[2]{x},\ \ \ \ \ \ \ \sqrt[8]{x^3} = x^{\frac{3}{8}} \\ \\
&\sqrt[4]{x^3} = x^{\frac{3}{4}},\ \ \ \ \ \ \ \sqrt[7]{x^{5}} = x^{\frac{5}{7}}
\end{align*}
Neu!
Kombination der Techniken
Bei dem Ausdruck $\frac{20}{\sqrt[3]{x}}$ sollte zunächst die Wurzel in $\frac{20}{x^{\frac{1}{3}}}$ umgeschrieben werden. Dann kann der Nenner von „unten“ nach „oben“ holen: $20 x^{-\frac{1}{3}}$. So lässt sich meist einfacher Rechnen.
Beispiel
Fasse den Ausdruck so weit wie möglich zusammen:
\begin{align*}
&\frac{7}{x} + \sqrt[3]{x} &= 7x^{-1} + x^{\frac{1}{3}}
\end{align*}
Häufige Stolperfallen:
\begin{align*}
&\frac{x}{2}=\frac{1}{2}x, \ \ \ \ \frac{x}{3}=\frac{1}{3}x, \ \ \ \ \frac{x^3}{7}=\frac{1}{7}x^3 \\ \\
&\frac{x}{a} = \frac{1}{a} x, \ \ \ \ \frac{3x}{a} = \frac{3}{a} x, \ \ \ \ \frac{x^3}{a} = \frac{1}{a} x^3
\end{align*}
Daniel erklärt euch das Thema Potenzen nochmal in seinem Video

