
Austauschprozesse
In diesem Artikel erfährst du alles zum Thema Austauschprozesse:
- Übergangsgraph/-diagramm
- Übergangsmatrix ablesen
- Zeitlich Vorwärtsrechnen
- Zeitlich Rückwärtsrechnen (mit LGS oder inverser Matrix)
- Begriff Fixvektor, stabiler Vektor
Austauschprozesse sind ein beliebtes Thema für eine Klausuraufgabe. Hierbei gibt es einige Dinge, die ihr beachten müsst.
In der Regel ist ein Übergangsgraph gegeben, aus dem ihr eine Matrix erstellen sollt. Achtet immer auf den Zeitraum, der angegeben ist. Das ist wichtig für eure Antworten (z.B. monatlich, Woche zu Woche etc.)!
Es kann auch sein, dass die Matrix gegeben ist und ihr den Übergangsgraphen zeichnen sollt. Am sinnvollsten ist es, als Zwischenschritt eine Tabelle aufzustellen, damit das Fehlerrisiko reduziert wird.
Im Folgenden werden wir die einzelnen Komponenten zum Thema Austauschprozesse erläutern.
Neu!
Übergangsgraph/-diagramm
Übergangsgraphen sind spezielle gerichtete Graphen mit sogenannten Kantengewichten, die eine Verbindung zwischen Stochastik und Graphentheorie schlagen. In der folgenden Abbildung ist ein Übergangsgraph bzw. ein Übergangsdiagramm dargestellt, der die wöchentliche Wahl des Lieblingsfaches darstellen soll. Wichtig ist die zeitliche Angabe – hier: wöchentlich! Aus diesem Graphen lässt sich eine Tabelle erstellen. Achte auf die Zuordnung: von – nach!
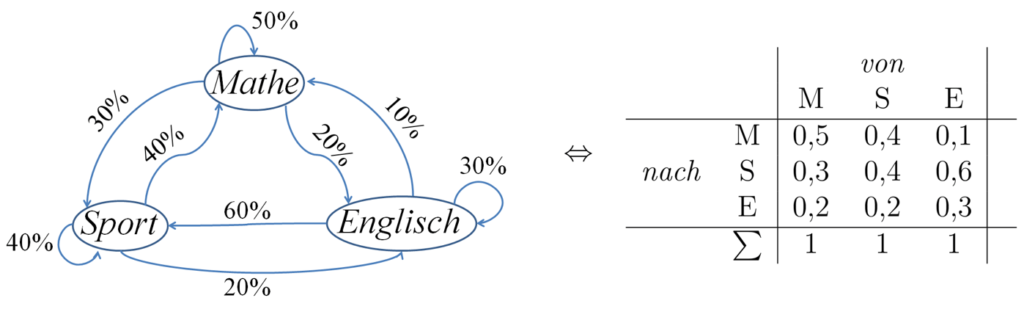
Wichtig hierbei ist, dass die Spaltensumme immer 1 ergeben muss! Wenn nicht, kontrolliert dann nochmal, ob ihr alles richtig gemacht habt.
Übergangsmatrix ablesen
Aus der Tabellenform nun auf die Übergangsmatrix $M$ kommen – die Matrix steht da quasi schon! Einfach die Zahlenwerte hinschreiben, Klammer drum und fertig!
Doch wie werden die Koeffizienten der Übergangsmatrix interpretiert? Wir betrachten die Koeffizienten $m_{11}$ und $m_{23}$ und versuchen diese zu interpretieren.

- $m_{11}$ – von Mathe zu Mathe: Schüler, die Mathe als Lieblingsfach gewählt hat, werden in der nächsten Woche mit einer 50-prozentigen Wahrscheinlichkeit wieder Mathe als Lieblingsfach wählen.
- $m_{23}$ – von Englisch zu Sport: Schüler, die Englisch als Lieblingsfach gewählt hat, werden in der nächsten Woche mit einer 20-prozentigen Wahrscheinlichkeit Sport als Lieblingsfach wählen.
Zeitlich Vorwärtsrechnen
Wenn wir nun wissen wollen, was in der nächsten Woche passiert, stellen wir folgende Gleichung auf:
\begin{align*}
\left( \begin{array}{ccc} 0,5 & 0,4 & 0,1 \\ 0,3 & 0,4 & 0,6 \\ 0,2 & 0,2 & 0,3 \end{array} \right) \cdot
\underbrace{\left( \begin{array}{c} m \\ s \\ e \end{array} \right)}_{{\textrm{Verteilung JETZT}}} =
\underbrace{\left( \begin{array}{c} m‘ \\ s‘ \\ e‘ \end{array} \right)}_{{\textrm{Verteilung beim nächsten Mal}}} \quad (1)
\end{align*}
Der Vektor $(m,s,e)^T$ gibt die Verteilung der Lieblingsfächer Mathe, Sport und Englisch zum Zeitpunkt „jetzt“ an. Oft findet ihr in Büchern oder Aufgaben eine allgemeinere Form:
\begin{align*}
\left( \begin{array}{ccc} \cdots & & \\ \vdots & \ddots & \\ & & \end{array} \right) \cdot
\left( \begin{array}{c} x \\ y \\ z \end{array} \right) =
\left( \begin{array}{c} x‘ \\ y‘ \\ z‘ \end{array} \right) \notag
\end{align*}
Wichtig ist, dass der Vektor $(x,y,z)^T$ die gleiche Reihenfolge wie in der Tabelle hat!
Was passiert, wenn wir die Verteilung beim übernächsten Mal $(x“ \ y“ \ z“)^T$ bestimmen wollen? Hier gibt es zwei Möglichkeiten:
- Möglichkeit
\begin{align*}M \cdot\left( \begin{array}{c} x \\ y \\ z \end{array} \right) =\left( \begin{array}{c} x‘ \\ y‘ \\ z‘ \end{array} \right) \quad \textrm{und dann} \cdot\left( \begin{array}{c} x‘ \\ y‘ \\ z‘ \end{array} \right) =\left( \begin{array}{c} x“ \\ y“ \\ z“ \end{array} \right) \notag\end{align*} - Möglichkeit – Übergangsmatrix $M$ im Vorfeld multiplizieren (siehe Abschnitt Matrix mal Matrix).
\begin{align*}M\cdot M = M^2 \quad \Rightarrow ^2 \cdot\left( \begin{array}{c} x \\ y \\ z \end{array} \right) =\left( \begin{array}{c} x“ \\ y“ \\ z“ \end{array} \right), \notag\end{align*}wobei wir bei der Interpretation der Koeffizienten der Übergangsmatrix $M^2$ aufpassen müssen. Diese beschreibt nun nicht mehr die wöchentlichen Übergangswahrscheinlich-keiten zur Wahl des Lieblingsfaches, sondern die für 2 Wochen! Der Zeitraum hat sich geändert.
Daniel fasst alles zum Thema Austauschprozesse nochmals in diesem Lernvideo zusammen.
httpv://www.youtube.com/watch?v=–hyMa4T0yM
Zeitlich Rückwärtsrechnen (mit LGS oder inverser Matrix)
Schau dir zur Wiederholung nochmal das Video zur inversen Matrix an.
Oder das Lernvideo zu Linearen Gleichungssystemen
Wie war es beim letzten Mal? Diese Frage kann theoretisch auch vorkommen und sollte für euch kein Problem darstellen. Bleiben wir bei unserem Beispiel mit dem Lieblingsfach. Die Übergangsmatrix $M$ entnehmen wir von oben, die Verteilung der Lieblingsfächer zum jetzigen Zeitpunkt sei 20 für Mathe, 10 für Sport, 3 bei Englisch. Wir betrachten nun Gl. (1) und tragen die gegebenen Werte wie folgt ein:
\begin{align*}
\left( \begin{array}{ccc} 0,5 & 0,4 & 0,1 \\ 0,3 & 0,4 & 0,6 \\ 0,2 & 0,2 & 0,3 \end{array} \right) \cdot
\underbrace{\left( \begin{array}{c} m \\ s \\ e \end{array} \right)}_{\textrm{Verteilung letzte Woche}} =
\underbrace{\left( \begin{array}{c} 20 \\ 10 \\ 3 \end{array} \right)}_{\textrm{Verteilung in dieser Woche}} \notag
\end{align*}
Wir haben nun folgende Möglichkeiten:
- LGS aufstellen und lösen – am einfachsten mit dem Taschenrechner!
- Gleichung $M \cdot \vec{x}_{vor} = \vec{x}$ umstellen zu $\vec{x}_{vor} = M^{-1} \cdot \vec{x} $! Hierfür benötigen wir die Inverse der Matrix $M$. Anschließend können wir die Verteilung zum letzten Mal sehr einfach ausrechnen.
Einschub: Inverse Matrix bestimmen
Wenn man eine Matrix $A$ mit ihrer inversen Matrix $A^{−1}$ multipliziert, entsteht die Einheitsmatrix. Denkt an die Welt der normalen Zahlen: Multipliziert man eine Zahl mit ihrem Kehrwert, lautet das Ergebnis stets 1. Was für Zahlen funktioniert, geht auch ähnlich bei der Matrix. Es gilt: $A \cdot A^{-1} = A^{-1} \cdot A=1$.
Im Wesentlichen gibt es zwei Verfahren zur Bestimmung der Inversen Matrix:
- Inverse bestimmen mit Hilfe des Gauß-Jordan-Algorithmus
- Invers bestimmen mit Hilfe der Adjunkten – nur sinnvoll bei $2 \times 2$ Matrizen!
\begin{align*}
A^{-1} = \frac{1}{|A|} \cdot Adj(A) \label{eq:InvAdj}
\end{align*}
Vorgehen:
(i) Berechne die Determinante von $A = \begin{pmatrix} {{a}} & {{b}}\\ {{c}} & {{d}} \end{pmatrix}$. Wenn die Determinante von $A$ gleich Null ist, gibt es keine Inverse und du kannst mit dem Rechnen aufhören.
(ii) Ist die Determinante von $A$ ungleich Null, berechne die Adjunkte.
\begin{align*}
\operatorname{adj} (A) = \begin{pmatrix} \,\,\,{{d}} & \!\!{{-b}}\\ {{-c}} & {{a}} \end{pmatrix} \notag
\end{align*}
(iii) Setze die Zwischenergebnisse in die Formel zur Berechnung der inversen Matrix ein
Nur quadratische Matrizen können eine Inverse besitzen. Jedoch existiert nicht für jede quadratische Matrix eine Inverse. Falls für eine Matrix $A$ die Inverse existiert, so heißt die Matrix regulär – andernfalls heißt sie singulär.
Rechenregeln:
- $\left(A \cdot B\right)^{-1} = B^{-1} \cdot A^{-1}$
- $\left(A^{T}\right)^{-1} = \left(A^{-1}\right)^{T}$
- $\left(A^{-1}\right)^{-1} = A$
- $\left(k \cdot A\right)^{-1} = k^{-1} \cdot A^{-1}$
Wenn wir eine $3 \times 3$ Matrix vorliegen haben, sollte man entweder seinen Taschenrechner bedienen können, oder den guten Gauß-Jordan-Algorithmus beherrschen.
Hier ein Beispiel:
Bestimme die Inverse zur reellen Matrix
\begin{align*}
A = \begin{pmatrix} 1 & 2 & 0 \\ 2 & 4 & 1 \\ 2 & 1 & 0 \end{pmatrix} \quad \Rightarrow \quad
\begin{array}{c} \textrm{I} \\ \textrm{II} \\ \textrm{III} \end{array}
\left(\begin{array}{ccc|ccc} 1 & 2 & 0 \, & \, 1 & 0 & 0 \\ { 2} & 4 & 1 \, & \, 0 & 1 & 0 \\ { 2} & 1 & 0 \, & \, 0 & 0 & 1 \end{array}\right) \notag
\end{align*}
Die Idee ist es, die Einheitsmatrix von der rechten Seite auf die linke Seite zu bringen. Das schaffen wir, in dem wir die linke Seite mit dem Additionsverfahren so zu verändern, dass nur auf der Diagonalen 1en stehen und sonst 0en.
Zunächst werden hier die beiden 2-en in der ersten Spalte eliminiert, indem wir $\textrm{II} – 2 \cdot \textrm{I}$ und $\textrm{III} – 2 \cdot \textrm{I}$ rechnen. Nachdem in der zweiten Spalte nun eine 0 steht, wird zur Elimination der -3 die zweite mit der dritten Zeile vertauscht und man erhält die obere Dreiecksform:
\begin{align*}
\rightarrow \left(\begin{array}{ccc|ccc} 1 & 2 & 0 \, & \, 1 & 0 & 0 \\ 0 & 0 & 1 \, & \, -2 & 1 & 0 \\ 0 & { -3} & 0 \, & \, -2 & 0 & 1 \end{array}\right) \rightarrow \left(\begin{array}{ccc|ccc} 1 & 2 & 0 \, & \, 1 & 0 & 0 \\ 0 & -3 & 0 \, & \, -2 & 0 & 1 \\ 0 & 0 & 1 \, & \, -2 & 1 & 0 \end{array}\right). \notag
\end{align*}
Nun muss lediglich die verbleibende 2 oberhalb der Diagonalen zu Null gesetzt werden, was durch Addition des Doppelten der zweiten Zeile zum Dreifachen der ersten Zeile geschieht. Schließlich muss noch die erste Zeile durch 3 und die zweite Zeile durch -3 dividiert werden und man erhält als Ergebnis:
\begin{align*}
\left(\begin{array}{ccc|ccc} 1 & 2& 0 \, & \, 1 & 0 & 0 \\ 0 & -3 & 0 \, & \, -2 & 0 & 1 \\ 0 & 0 & 1 \, & \, -2 & 1 & 0 \end{array}\right) \rightarrow \left(\begin{array}{ccc|ccc} { 3} & 0 & 0 \, & \, -1 & 0 & 2 \\ 0 & { -3} & 0 \, & \, -2 & 0 & 1 \\ 0 & 0 & 1 \, & \, -2 & 1 & 0 \end{array}\right) \rightarrow \left(\begin{array}{ccc|ccc} 1 & 0 & 0 \, & \, -\tfrac13 & 0 & \tfrac23 \\ 0 & 1 & 0 \, & \, \tfrac23 & 0 & -\tfrac13 \\ 0 & 0 & 1 \, & \, -2 & 1 & 0 \end{array}\right). \notag
\end{align*}
Die Inverse von $A$ ist demnach:
\begin{align*}
A^{-1} = \begin{pmatrix} -\tfrac13 & 0 & \tfrac23 \\ \tfrac23 & 0 & -\tfrac13 \\ -2 & 1 & 0 \end{pmatrix} = \frac{1}{3} \begin{pmatrix} -1 & 0 & 2 \\ 2 & 0 & -1 \\ -6 & 3 & 0 \end{pmatrix}. \notag
\end{align*}
Neu!
Begriff Fixvektor, stabiler Vektor
Ein Fixvektor beschreibt einen stabilen Zustand, also einen Zustand, der sich durch Anwenden der Übergangsmatrix nicht mehr ändert. Dieser Zustand wird auch „stationärer“ Zustand genannt. Häufig wird in Aufgaben verlangt, den Fixvektor zu einem gegebenem System zu bestimmen bzw. erst seine Existenz zu überprüfen.
Mathematisch betrachtet ist der Vektor $\vec{v}=(a\ b\ c)^T$ gesucht, für den gilt $M\cdot \vec{v} = \vec{v}$. Dieser kann (wenn es ihn denn gibt) aus dem zugehörigen Gleichungssystem allgemein bestimmt werden. In einem zweiten Schritt kann dann der zu einem gegebenen Zustandsvektor $\vec{v_0} = (150\ 240\ 120)^T$ gehörige Fixvektor bestimmt werden.
Beispiel:
Gegeben sei folgende Übergangsmatrix $M$. Der Fixvektor ist gesucht.
\begin{align*}
M = \begin{pmatrix} 0,6 & 0,05 & 0,3 \\ 0,1 & 0,8 & 0,2 \\ 0,3 & 0,15 & 0,5 \end{pmatrix} \notag
\end{align*}
Aus der Bedingung $M\cdot \vec{v} = \vec{v}$ ergibt sich das folgende Gleichungssystem:
\begin{align*}
\begin{array}{rcrcrcll}
0,6 a &+& 0,05 b &+& 0,3 c &= &a & |-a \\
0,1 a &+& 0,8 b &+& 0,2 c &=& b & |-b \\
0,3 a &+& 0,15 b &+& 0,5 c &=& c & |-c
\end{array}
\Leftrightarrow
\begin{array}{rcrcrcl}
-0,4 a &+& 0,05 b &+& 0,3 c &= &0 \\
0,1 a &-& 0,2 b &+& 0,2 c &=&0 \\
0,3 a &+& 0,15 b &-& 0,5 c &=& 0
\end{array}
\end{align*}
Wenn wir versuchen das LGS zu lösen, sei es per Hand oder mit dem TR, bekommen wir keine eindeutige Lösung heraus, sondern alles in Abhängigkeit einer Unbekannten.
Wichtig: Es gibt nur dann eine stationäre Verteilung, wenn die Lösung des Gleichungssystems eine wahre Aussage ist, z.B. $0=0$!
Wir geben die Lösung also in Abhängigkeit eines Parameters, hier $c$, an und erhalten damit den allgemeinen Fixvektor:
\begin{align*}
\vec{v} = \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \begin{pmatrix} \frac{14}{15}~c \\[0.2cm] \frac{22}{15}~c \\ c \end{pmatrix} \notag
\end{align*}
Den zu unserem Zustandsvektor $\vec{v}_0$ gehörende Fixvektor bekommen wir, indem wir die Informationen aus $\vec{v}_0$ als weitere Gleichung dazu nehmen.
Es gilt
\begin{align*}
a + b + c = 150 + 240 + 120 = 510 \quad \textrm{und damit auch} \quad \frac{14}{15}c + \frac{22}{15}c + c = 510 \notag
\end{align*}
Wenn wir die Gleichung nach $c$ auflösen erhalten wir für $c=150$ und damit den Fixvektor $\vec{v}_F$ zum Zustandsvektor $\vec{v}_0$
\begin{align*}
\vec{v_{F}}= \begin{pmatrix}
140 \\ 220 \\ 150
\end{pmatrix}.
\end{align*}
Eine weitere Möglichkeit den Fixvektor zu bestimmen, ist die wiederholte Multiplikation der Übergangsmatrix mit sich selbst. Wenn sich die Werte der Matrix stabilisieren, kann man Spaltenweise den Fixvektor ablesen.
Beispiel:
\begin{align*}
M^{100} = \begin{pmatrix} 0,5 & 0,5 & 0,5 \\ 0,2 & 0,2 & 0,2 \\ 0,3 & 0,3 & 0,3 \end{pmatrix} \quad \Rightarrow \vec{v}=\begin{pmatrix}
0,5 \\ 0,2 \\ 0,3
\end{pmatrix}
\end{align*}
Beispielaufgabe Austauschprozesse:
Eine Personengruppe wird jedes Jahr nach ihrem Lieblingsgetränk zum Frühstück gefragt. Zur Auswahl stehen Kaffee, Tee und Saft. Aus den letzten Jahren wurden folgende Beobachtungen gemacht: Von den Kaffeetrinkern trinken im darauffolgenden Jahr 80% weiter Kaffee, 10% Tee und 10% Saft. Von den Teetrinkern trinken 70% weiter Tee, 20% Kaffee und 10% Saft. Von den Safttrinkern trinken 50% weiter Saft, 30% Kaffee und 20% Tee.
a) Stelle ein Übergangsdiagramm und die dazugehörige Matrix in der Reihenfolge Kaffee $K$, Tee $T$ und Saft $S$ auf.
b) In diesem Jahr haben von 1000 Menschen 650 Kaffee, 200 Tee und 150 Saft getrunken. Wie sieht die Verteilung im nächsten Jahr und im vorherigem Jahr aus?
c) Bestimme den Fixvektor des Austauschprozesses.
Lösungen:
a)
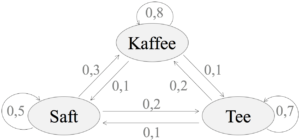
$\Downarrow$
$
\renewcommand{\arraystretch}{1.3}
\begin{array}{r|ccc}
& K & T & S \\
\hline
K & 0,8 & 0,2 & 0,3 \\
T & 0,1 & 0,7 & 0,2 \\
S & 0,1 & 0,1 & 0,5 \\
\end{array}$
$\Downarrow$
$M=\begin{pmatrix}
0,8 & 0,2 & 0,3 \\
0,1 & 0,7 & 0,2 \\
0,1 & 0,1 & 0,5
\end{pmatrix}$
b)
Verteilung in diesem Jahr:
$V= \begin{pmatrix}
650 \\ 200 \\ 150
\end{pmatrix}$
Verteilung im nächsten Jahr:
$V’=M \cdot V= \begin{pmatrix}
0,8 & 0,2 & 0,3 \\
0,1 & 0,7 & 0,2 \\
0,1 & 0,1 & 0,5
\end{pmatrix} \cdot \begin{pmatrix}
650 \\ 200 \\ 150
\end{pmatrix}=\begin{pmatrix}
605 \\ 235 \\ 160
\end{pmatrix}$
Verteilung im vorherigen Jahr, mit dem Ansatz $M\cdot \vec{x}=V$:
\begin{align*} \begin{pmatrix}
0,8 & 0,2 & 0,3 \\
0,1 & 0,7 & 0,2 \\
0,1 & 0,1 & 0,5
\end{pmatrix} \cdot \begin{pmatrix}
x \\ y \\ z
\end{pmatrix}=\begin{pmatrix}
650 \\ 200 \\ 150
\end{pmatrix} \ \Rightarrow \ \begin{array}{rrcrcrcl}
\textrm{I} & 0,8x & + & 0,2y & + & 0,3z & = & 650 \\
\textrm{II} & 0,1x & + & 0,7y & + & 0,2z & = & 200 \\
\textrm{III} & 0,1x & + & 0,1y & + & 0,5z & = & 150
\end{array}
\end{align*}
Das LGS liefert die eindeutige Lösung x=729,17, y=145,83 und z=125. Damit war die Verteilung im vorherigen Jahr $V^*=(729 \ 146 \ 125)^T$.
c)
Der Fixvektor muss die Bedingung $M \cdot \vec{x}=\vec{x}$ erfüllen:
\begin{align*} \begin{pmatrix}
0,8 & 0,2 & 0,3 \\
0,1 & 0,7 & 0,2 \\
0,1 & 0,1 & 0,5
\end{pmatrix} \cdot \begin{pmatrix}
x \\ y \\ z
\end{pmatrix}=\begin{pmatrix}
x \\ y \\ z
\end{pmatrix} \ \Rightarrow \ \begin{array}{rrcrcrcl}
\textrm{I} & 0,8x & + & 0,2y & + & 0,3z & = & x \\
\textrm{II} & 0,1x & + & 0,7y & + & 0,2z & = & y \\
\textrm{III} & 0,1x & + & 0,1y & + & 0,5z & = & z
\end{array} \end{align*}
Wir erhalten keine eindeutige Lösung und geben in Lösung in Abhängigkeit der Variablen z an:
$x=\frac{13}{4} z, \ y=\frac{7}{4}z, \ z=z$
Mit der Bedingung, dass wir 1000 Personen haben, bekommen wir eine zusätzliche Gleichung, mit der wir z bestimmen können:
$x+y+z=1000 \ \Rightarrow \ \frac{13}{4} z + \frac{7}{4}z + z = 1000 \ \Leftrightarrow \ z=166 \frac{2}{3}$
Daraus ergibt sich der Fixvektor:
\begin{align*} \vec{v}_F=\begin{pmatrix}
541\frac{2}{3} \\ 291\frac{2}{3} \\ 166\frac{2}{3}
\end{pmatrix} \end{align*}
Neu!

