
Bedingte Wahrscheinlichkeit und Unabhängigkeit
Du willst mehr erfahren zum Thema Bedingte Wahrscheinlichkeit und Unabhängigkeit? Wir erklären dir auf dieser Seite anhand von Aufgaben und Videos alles was du wissen musst.
Neu!
Bei der Berechnung von Wahrscheinlichkeiten bei Laplace-Experimenten kann man manchmal eine gegebene Zusatzinformation $B$ nutzen. Die mit der Vorinformation $B$ berechnete Wahrscheinlichkeit wird bedingte Wahrscheinlichkeit von $A$ unter der Bedingung $B$ genannt und mit $P(A|B)$ (oft auch $P_B(A)$) abgekürzt.
\begin{align*}
P(A|B)=\frac{P(A \cap B)}{P(B)}, \quad P(B) > 0
\end{align*}
Betrachten wir die Formel etwas genauer und machen uns klar, was diese beinhaltet:
$P$(Was suchen wir $|$ Was wissen wir bzw. was ist schon eingetreten).
In der Aufgabenstellung wird die Bedingung, also das was wir wissen, immer klar durch die Phrasen/Wörter „unter der Bedingung“, „wenn“, „obgleich“.
Analog lässt sich die bedingte Wahrscheinlichkeit P(B|A) gemäß
\begin{align*}
P(B|A)=\frac{P(A\cap B)}{P(A)} \notag
\end{align*}
errechnen.
Wichtig: Nutze zur Vereinfachung eine Vierfeldertafel um die Wahrscheinlichkeiten zu bestimmen.
Vierfeldertafel
Eine Vierfeldertafel eignet sich zur Bestimmung von Wahrscheinlichkeiten der Verknüpfungen zweier Ereignisse $A$ und $B$. Unten sehen wir eine allgemeine Vierfeldertafel.
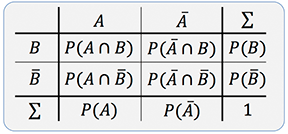
Hinweis: In den Feldern können auch absolute Häufigkeiten stehen.
Satz von Bayes
Zwischen den bedingten Wahrscheinlichkeiten $P(A|B)$ und $P(B|A)$ besteht die auch als Satz von Bayes bezeichnete Beziehung:
\begin{align*}
P(A|B)=\frac{P(B | A) \cdot P(A)}{P(B)}= \frac{P(B | A) \cdot P(A)}{P(A) \cdot P(B|A) + P(\bar{A}) \cdot P(B|\bar{A})} \notag
\end{align*}
Der Satz von Bayes wird verwendet, wenn man das Ergebnis schon kennt und die Wahrscheinlichkeiten für eine mögliche Ursache herausfinden möchte. Wenn man die Gleichung näher betrachtet, sollte uns $P(A|B)= P$(Was suchen wir $|$ Was wissen wir) bekannt vorkommen. Ferner steht im Nenner der Satz der totalen Wahrscheinlichkeit, welcher die Summe der möglichen Ausgänge darstellt.
Stochastische Unabhängigkeit
Zwei zufällige Ereignisse $A$ und $B$ werden als unabhängig oder auch als stochastisch unabhängig bezeichnet, wenn das Eintreten eines Ereignisses keinen Einfluss auf das andere Ereignis hat.
Zwei Ereignisse $A$, $B$ mit $P(A) > 0$ und $P(B) >0$ heißen unabhängig, wenn eine der folgenden äquivalenten Bedingungen gilt:
\begin{align*}
P(A \cap B)=P(A) \cdot P(B)
\end{align*}
Wichtig: Die Unabhängigkeit darf nicht verwechselt werden mit der Unvereinbarkeit zweier Ereignisse:
- Unabhängigkeit: $P(A \cap B) = P(A) \cdot P(B)$
- Unvereinbarkeit: $A \cap B = \{ \}$
In einer Schule werden neben dem Unterricht ein Förderkurs und eine AG angeboten. 70% der Schüler besuchen keinen Förderkurs und 40% der Schüler keine AG. 25% der Schüler nehmen weder an dem Förderkurs noch an der AG teil.
Alle Informationen des Aufgabentextes haben wir zunächst übersichtlich in eine Vierfeldertafel geschrieben. Das ist der erste Schritt, den ihr machen solltet, wenn es um bedingte Wahrscheinlichkeiten geht.
\renewcommand{\arraystretch}{1.3}
\begin{array}{c|c|c|c}
& F & \overline{F} & \sum \\
\hline
AG & 0,15 & 0,45 & 0,6 \\
\hline
\overline{AG} & 0,15 & 0,25 & 0,4 \\
\hline
\sum & 0,3 & 0,7 & 1
\end{array}
$
Wie groß ist die Wahrscheinlichkeit, dass
1. ein Schüler den Förderkurs nicht wählt, unter der Bedingung, dass er auch keine AG besucht?
Aus der Aufgabenstellung müssen wir die Bedingung identifizieren, in dem man auf die Signalwörter („unter der Bedingung“, „wenn“, „obgleich“) achtet. Mit der Kenntnis, welches Ereignis bereits eingetreten ist, folgt:
\begin{align*}
P(\textrm{Was suchen wir}|\textrm{Was wissen wir})=P(\overline{F}|\overline{AG})
\end{align*}
Im nächsten Schritt berechnen wir mit der Formel der bedingten Wahrscheinlichkeit die gesuchte Wahrscheinlichkeit.
\begin{align*}
P(\overline{F}|\overline{AG}) = \frac{P(\overline{F} \cap \overline{AG} )}{P(\overline{AG})}=\frac{0,25}{0,4}=0,625
\end{align*}
2. ein Schüler die AG nicht wählt, unter der Bedingung, dass er auch keinen Förderkurs besucht?
\begin{align*}
P(\overline{AG}|\overline{F}) = \frac{P(\overline{AG} \cap \overline{F} )}{P(\overline{F})}=\frac{0,25}{0,7}=0,3571
\end{align*}
3. ein Schüler die AG wählt, unter der Bedingung, dass er schon den Förderkurs gewählt hat?
\begin{align*}
P(AG|F) = \frac{P(AG \cap F )}{P(F)}=\frac{0,15}{0,3}=0,5
\end{align*}
4. Sind die Ereignisse unabhängig?
Wir verwenden die Formel $P(A \cap B)$=$P(A) \cdot P(B)$ und setzen die für uns passenden Ereginisse ein. Es folgt:
\begin{align*}
P(F \cap AG) &= P(F) \cdot P(AG) \\
0,15 &= 0,3 \cdot 0,6 \\
0,15 &\neq 0,18
\end{align*}
In dem Beispiel sind die beiden Ereignisse voneinander abhängig, also nicht stochastisch unabhängig. Demnach wählt ein Schüler den Förderkurs (Förderkurs nicht) abhängig davon ob er die AG (AG nicht) wählt.
Neu!
Vertiefend findest du in Daniels Playlist weitere Videos zum Thema Bedingte Wahrscheinlichkeit.

