
Dreisatz
Der Dreisatz ist eines der wichtigsten Lösungsverfahren in der Mathematik. Mit dem Dreisatzes können wir Aufgaben lösen, in denen zwei Größen proportional oder antiproportional zueinander sind. Die Bezeichnung Dreisatz ergibt sich aus den drei Rechenschritten die dafür benötigt werden das Ergebnis auszurechnen.
Inhaltsverzeichnis
- Dreisatz – proportionale Zuordnung
- Dreisatz – antiproportionale Zuordnung
- Wann proportionale- und wann antiproportionale Zuordnung?
NEU
Dreisatz – proportionale Zuordnung
Beim Dreisatz wird einer bestimmten Menge oder Größe (z.B. kg Fleisch) eine weitere Menge oder Größe zugeordnet (z.B. Preis pro kg Fleisch). In diesem Fall handelt es sich um einen proportionalen Zusammenhang, denn es gilt: je mehr Fleisch ich kaufe, desto mehr muss ich bezahlen.
Beim umgekehrten Dreisatz wird ebenfalls einer Mege oder Größe eine weitere Menge oder Größe zugeordnet. Hierbei gilt jedoch anders als beim proportionalen zusammenhang folgendes: je mehr Bagger arbeiten, desto weniger Arbeitszeit wird benötigt. Dieser umgekehrte Dreisatz wird auch antiproportionaler Zusammenhang genannt.

Ihr müsst euch die Aufgaben zum Dreisatz sorgfältig durchlesen und entscheiden, ob es sich um einen proportionalen- oder antiproportionalen Zusammenhang handelt.
Dazu wollen wir uns ein paar Beispiele angucken:
Durchschnittliche Geschwindigkeit & Fahrtdauer
Hierbei handelt es sich um den umgekehrter Dreisatz. Es gilt: je höher die durchschnittliche Geschwindigkeit, desto geringer die Fahrtdauer bis zur Ankunft.
Fahrtstrecke & Taxipreis
Hierbei handelt es sich um den klassischen Dreisatz. Es gilt: je länger die zu fahrende Strecke, desto höher wird der Taxipreis.
Lebensalter & Körperlänge
Im ersten Moment könnten wir denken, dass es sich um eine proportionale Zuordnung handelt. Aber manche Menschen wachsen bis zum 14. Lebensjahr vielleicht viel und wiederum andere wenig.
Ebenfalls kann es sein, dass manche Menschen schon ab dem 65. Lebensjahr an Körperlänge verlieren, andere wiederum erst mit dem 80. Lebensjahr.
Es gibt für diese Zuordnung also kein eindeutiges Muster, nach dem wir die Körperlänge für ein bestimmtes Lebensalter bestimmen können. Passt also gut auf, denn hin und wieder kommt es vor, dass man euch eine Falle stellt, indem die ausgesuchte Zuordnung weder proportional noch antiproportional ist.
Du hast den Dreisatz noch nicht ganz verstanden? Lass ihn dir nochmal von Daniel erklären!
Dreisatz Übungsaufgabe
Als nächstes wollen wir uns angucken, wie man Aufgaben zu proportionalen Zuordnungen mit Hilfe des Dreisatz’ lösen kann. Dazu schauen wir uns die folgende Aufgabe an.
Aufgabenstellung:
3kg feinstes Rinderfilet kosten 147€. Peter und Susanne brauchen, weil sie die ganze Familie zum Essen einladen wollen, 7kg Fleisch. Wie teuer sind 7kg feinstes Rinderfilet?
Herangehensweise:
Wir werden uns jetzt verschieden Wege und Schreibweisen angucken, mit denen wir solch eine Aufgabe lösen können. Ihr könnt euch dann den Lösungsweg heraussuchen, welcher für euch am besten geeignet ist.
Die wohl am häufigsten vorkommende Methode ist der Dreisatz innerhalb einer Tabelle.
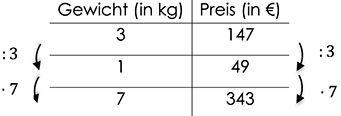
Wir erstellen also eine Tabelle mit zwei Spalten und tragen links das Gewicht- und rechts den Preis ein. Direkt in der Zeile da drunter unsere bekannten Werte:
![]()
Als nächstes überlegen wir uns, wie wir den Preis für 7kg berechnen können. Wir kommen nicht durch eine einfache Multiplikation direkt von den 3kg zu den 7kg. Aber wir könnten ja in einem Zwischenschritt den Preis für 1kg Rinderfilet berechnen. Dazu teilen wir auf beiden Seiten unserer Tabelle durch 3.

Jetzt wissen wir also, dass 1kg Rinderfilet 49€ kostet.
Wir möchten aber wissen, wie teuer 7kg Rinderfilet sind. Dazu multiplizieren wir auf beiden Seiten mit 7:

Lösung:
7kg feinstes Rinderfilet kosten also 343€.
NEU
Rechnen wir ein weiteres Beispiel
Aufgabenstellung:
15kg feinstes Schweinefilet kosten 70€ und Susanne benötigt 9kg. Wie teuer sind die 9kg feinstes Schweinefilet?
Herangehensweise:
Ihr müsst nicht immer die Zahl 1 als Zwischenschritt wählen, unter Umständen kann man mit anderen Werten einfacher rechnen:
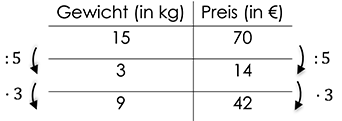
In diesem Beispiel ist der Wert 3 also ein besser geeigneter Zwischenschritt. Hätten wir hier die 1 als Zwischenschritt gewählt, würde die Division auf der rechten Seite $\mathrm{70:15=}\frac{\mathrm{14}}{\mathrm{3}}$ ergeben. 9kg Schweinefilet kosten also 42€.
Es ist ebenfalls möglich, eine solche Aufgabe durch die Zuhilfenahme einer Bruchgleichung zu lösen:
\[\frac{15\ kg}{70\ \textrm{€}}=\frac{9\ kg}{x\ \textrm{€}}\]
Damit unsere Gleichung möglichst einfach aussieht und ihr nicht auf Grund der Einheiten durcheinander kommt, lassen wir die Einheiten ab dem nächsten Schritt weg.
Wir können jetzt unseren vorhin erwähnten Trick anwenden und bilden auf beiden Seiten unserer Gleichung den jeweiligen Kehrwert. Im Anschluss multiplizieren wir direkt mit 9:
\[\frac{70\textrm{€}\ }{15kg\ }=\frac{x\ }{9kg\ } |\cdot 9\]
\[\frac{70\textrm{€}\ \ \cdot \ 9kg\ }{15kg\ }\ =x\]
Jetzt müssen wir den Term auf der linken Seite nur noch ausrechnen und erhalten:
\[42\textrm{€}=x\]
Lösung:
Es kommt das gleiche Ergebnis wie oben raus. 9kg Schweinefilet kosten 42€.
Manchmal ist es hilfreich zu wissen, ob es sich bei einer Zuordnung tatsächlich um eine proportionale Zuordnung handelt.
Zur Überprüfung kann die sogenannte Quotientengleichheit zu Rate gezogen werden. Dabei wird zeilenweise der Quotient gebildet und hinterher geguckt, ob alle Rechnungen denselben Wert ergeben haben.
Wir wollen das jetzt anhand unserer vorherigen Aufgabe überprüfen:
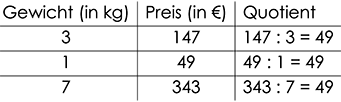
Wir sehen, dass unsere Berechnungen immer das Ergebnis 49 liefern. Es handelt sich also um eine proportionale Zuordnung. Es spielt übrigens keine Rolle, ob ich die linke Seite durch die rechte Seite oder die rechte Seite durch die linke Seite teile.
Schau dir zur Vertiefung direkt nochmal Daniels Video an!
Dreisatz – antiproportionale Zuordnung
Im folgenden Kapitel wollen wir uns angucken, worauf geachtet werden muss, wenn Aufgaben zu antiproportionalen Zuordnungen mit Hilfe des umgekehrten Dreisatz’ gelöst werden sollen. Dazu werfen wir einen Blick auf die folgende Aufgabe.
Aufgabenstellung:
10 Bagger benötigen 20 Stunden um eine bestimmte Menge Erde abzutransportieren. Es stehen jetzt aber lediglich 5 Bagger zur Verfügung. Wie viele Stunden brauchen diese 5 Bagger um die gleiche Menge Erde abzutransportieren?
Herangehensweise:
Wir stellen fest, dass es sich um den umgekehrter Dreisatz handelt, denn je weniger Bagger zur Verfügung stehen, desto mehr Stunden werden zum Abtransport benötigt.
Hier benutzen wir eine Tabelle und den umgekehrten Dreisatz, um unsere Aufgabe zu lösen:

Wir möchten wissen wie viele Stunden 5 Bagger zum Abtransport benötigen. So teilen wir die linke Seite der Tabelle durch 2 und erhalten $10\div 2=5$.
Auf der rechten Seite unserer Tabelle müssen wir mit 2 multiplizieren:

Lösung:
Wir sehen, dass 5 Bagger, also halb so viele Bagger wie ursprünglich, die doppelte Zeit brauchen um die Erde abzutransportieren. Wir merken uns, dass wir bei antiproportionalen Zuordnungen auf der gegenüberliegenden Seite immer mit dem Gegenteil rechnen müssen.
Auch antiproportionale Zuordnungen können auf ihre Richtigkeit überprüft werden. Dazu wird die sogenannte Produktgleichheit zu Rate gezogen. Dabei wird zeilenweise multipliziert und anschließend kontrolliert ob die berechneten Ergebnisse übereinstimmen:

Wir sehen, dass unsere Produkte jeweils den Wert 200 annehmen. Es handelt sich folglich um eine antiproportionale Zuordnung. Auf diese Art und Weise kann jede beliebige antiproportionale Zuordnung auf ihre Richtigkeit untersucht werden.
Beispielaufgabe 1
Aufgabenstellung:
Eine Bürofachangestellte benötigt für das Schreiben eines Briefes 12 Minuten und schreibt dabei durchschnittlich 250 Zeichen pro Minute. Wie lange benötigt eine andere Bürofachangestellte für denselben Brief, wenn sie durchschnittlich 300 Zeichen pro Minute schreibt?
Lösung:
Die Bürofachangestellte schreibt 12 Minuten lang 250 Zeichen. Der Brief hat demnach eine Länge von 12∙250=3000 Zeichen. Eine andere Bürofachangestellte schafft sogar 300 Zeichen pro Minute. Sie benötigt für das Schreiben des Briefes demnach 3000÷300=10 Minuten. Anmerkung: Je mehr Zeichen pro Minute geschrieben werden, desto weniger Zeit wird für das Schreiben des Briefes benötigt.
Beispielaufgabe 2
Aufgabenstellung:
Carlo fährt mit seinem Motorrad von Paderborn nach Beckum. Er benötigt für die 80km lange Strecke normalerweise 64 Minuten. Heute hat er nach 20km eine Panne. Wie viel Zeit ist bis dahin vergangen? Notiere Deine Rechnung.
Lösung:
Zuerst überlegen wir uns, ob es sich um eine proportionale oder eine antiproportionale Zuordnung handelt. Je mehr Kilometer Carlo fährt, desto mehr Zeit benötigt er dafür, es handelt sich also um eine proportionale Zuordnung. Grundsätzlich lassen sich alle Aufgaben zum Thema Zuordnungen immer mit einer Dreisatztabelle lösen. Das ist einfach und übersichtlich. Wir tragen zuerst unsere bekannten Daten in eine Dreisatztabelle ein:
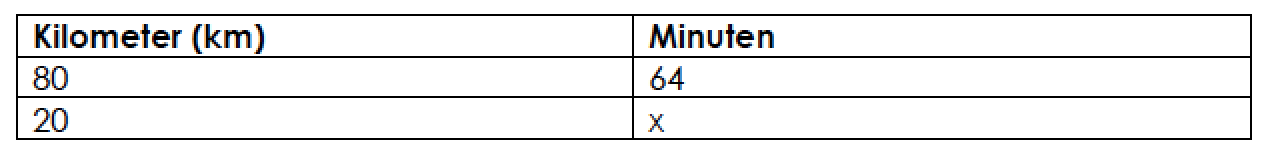
Jetzt überlegen wir uns, mit welcher Rechnung wir ganz einfach auf der linken Seite von der 80 zu der 20 gelangen:
\begin{align*}
80 / 4 = 20
\end{align*}
Da es sich hier um eine proportionale Zuordnung handelt, müssen wir auf beiden Seiten durch 4 teilen:
\begin{align*}
64 / 4 = 16
\end{align*}

Carlo war bis zur Panne bereits 16 Minuten unterwegs.
Schau dir am Ende zur Vertiefung die Playlist von Daniel zum Thema Dreisatz an.
Wann proportionale- und wann antiproportionale Zuordnung?
Der Unterschied zwischen proportionalen und antiproportionalen Zuordnungen wird anhand von praktischen Vergleichen schnell deutlich!
Proportional
- Je mehr V-Bucks ich kaufe, desto mehr Geld muss ich ausgeben.
- Je weniger V-Bucks ich kaufe, desto weniger Geld muss ich ausgeben.
Antiproportional
- Je mehr Leute beim Aufräumen helfen, desto weniger Zeit zum Aufräumen wird benötigt.
- Je weniger Leute beim Aufräumen helfen, desto mehr Zeit zum Aufräumen wird benötigt.
