
Ebenen in der Vektorrechnung
In diesem Artikel behandeln wir das Thema Ebenen in der Vektorrechnung. Du findest in den folgenden Abschnitten leicht verständliche Erklärungen, Beispiele und Lernvideos, mit denen du das Thema Ebenen in der Vektorrechnung schnell verstehen wirst.
Inhaltsverzeichnis
- Parameterdarstellung einer Ebene
- Ebenengleichung aufstellen
- Normalenvektor einer Ebene
- Punktprobe Ebene
- Spurpunkte mit Koordinatenachsen
1,99€
Parameterdarstellung einer Ebene
Die allgemeine Gleichung einer Ebene $E$ mit dem Stützvektor (auch Ortsvektor/Pin) $\vec{p}$ und den Richtungsvektoren (auch Spannvektoren) $\vec{u}$ und $\vec{v}$ lautet:
\begin{align*}
E:\vec{x}= \vec{p} + r \cdot \vec{u} + s \cdot \vec{v} \quad \textrm{mit} \ r,s \in \mathbb{R} \notag
\end{align*}
Für ein konkretes Beispiel sieht das wie folgt aus: Gegeben sind die Punkte $A, \ B$ und $C$ und wir stellen eine Ebene auf. Zunächst suchen wir uns einen Ortsvektor aus – hier sei es $A$! Für die Spannvektoren bilden wir $\overrightarrow{AB}$ und $\overrightarrow{AC}$ und schon haben wir die Parameterdarstellung der gesuchten Ebene.
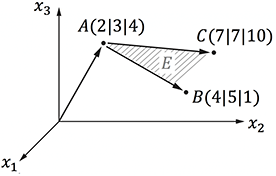
\begin{array}{c} 2 \\ 3 \\ 4
\end{array} \right)}_{\overrightarrow{0A}=\vec{a}} + r \cdot \underbrace{\left(
\begin{array}{c} 2 \\ 2 \\ -3 \end{array} \right)}_{\overrightarrow{AB}} + s \cdot \underbrace{\left( \begin{array}{c} 5 \\ 4 \\ 6
\end{array} \right)}_{\overrightarrow{AC}}$$
Wichtig: Die Richtungsvektoren der Ebene dürfen keine Vielfache voneinander sein, denn dann wäre es nur eine Gerade und keine Ebene!
Schau dir das Lernvideo zu Parameterform einer Ebene an.
Ebenengleichung aufstellen

1,99€
Normalenvektor einer Ebene
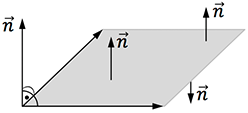
Der Normalenvektor $\vec{n}=(n_1 \ n_2 \ n_3)^T$ verläuft immer senkrecht (orthogonal) zur Ebene. Also senkrecht sowohl zum einen Richtungsvektor als auch zum anderen Richtungsvektor!
Anhand der Ebene $E$ zeigen wir euch zwei Möglichkeiten, wie man den Normalenvektor bestimmen kann.
\begin{align*}
E : \vec{x} = \left( \begin{array}{c} 2 \\ 1 \\ 3 \end{array} \right)
+ r \cdot \left( \begin{array}{c} 1 \\ 2 \\ 1 \end{array} \right)
+ s \cdot \left( \begin{array}{c} 2 \\ 2 \\ -1 \end{array} \right) \notag
\end{align*}
Möglichkeit 1: Skalarprodukt
\begin{align*}
\textrm{I} \quad \left( \begin{array}{c} n_1 \\ n_2 \\ n_3 \end{array} \right) \bullet \left( \begin{array}{c} 1 \\ 2 \\ 1 \end{array} \right) = 0 \quad \textrm{und} \quad
\textrm{II} \quad \left( \begin{array}{c} n_1 \\ n_2 \\ n_3 \end{array} \right) \bullet \left( \begin{array}{c} 2 \\ 2 \\ -1 \end{array} \right) = 0
\end{align*}
Wir erhalten ein lineares Gleichungssystem mit 2 Gleichungen und 3 Unbekannten. Da mehr Unbekannte vorliegen als Gleichungen ist das LGS nicht eindeutig lösbar!
\begin{align*}
\textrm{I} \quad 1n_1 + 2n_2 + 1 n_3 = 0 \notag \\
\textrm{II} \quad 2n_1 + 2n_2 – 1 n_3 = 0 \notag
\end{align*}
Es gibt hier zwei Berechnungsmöglichkeiten – per Hand oder per Taschenrechner. Wollt ihr das Gleichungssystem per Hand lösen, würde es sich in diesem Fall anbieten Gl. $\textrm{I}$ und $\textrm{II}$ zu addieren, damit $n_3$ wegfällt. Wir erhalten mit
\begin{align*}
& \quad & 3n_1 + 4n_2 \ &=0 \quad & |-4n_2 \\
& \Leftrightarrow \quad & 3n_1 \ &= -4n_2 \quad & \ |:(-4) \\
& \Leftrightarrow \quad & -\frac{3}{4} n_1 \ &= n_2 \quad &
\end{align*}
den allgemeinen Normalenvektor in Abhängigkeit von $n_1$: $\vec{n}=(n_1 \ -3/4n_1 \ 1/2n_1)^T$.
Für einen speziellen Normalenvektor wählen wir für $n_1$ eine beliebige Zahl aus. Die wählen wir so, dass insgesamt schöne Zahlen raus kommen. Wenn $n_1=4$ ist, dann folgt für $n_2=-3$ und für $n_3=2$. Daraus folgt für den speziellen Normalenvektor $\vec{n} = (4 \ -3 \ \ 2)^T$.
Möglichkeit 2: Kreuzprodukt
\begin{align*}
\left( \begin{array}{c} 1 \\ 2 \\ 1 \end{array} \right) \times
\left( \begin{array}{c} 2 \\ 2 \\ -1 \end{array} \right) = \left( \begin{array}{rcl} 2\cdot (-1) & – & 1 \cdot 2 \\ 1\cdot 2 & – & 1 \cdot (-1) \\ 1\cdot 2 & – & 2 \cdot 2 \end{array} \right) = \left( \begin{array}{c} -4 \\ 3 \\ -2 \end{array} \right) = \vec{n}
\end{align*}
Merke
Sucht man den Normalenvektor, so erhält man immer unendlich viele Lösungen, weil der Normalenvektor, egal welche Länge er hat, immer noch senkrecht zu den beiden Richtungsvektoren steht. Die verschiedenen Lösungen für $\vec{n}$ kommen also von den verschiedenen Richtungen und Längen von $\vec{n}$. Der Normalenvektor $\vec{n}$ mit Länge 1 heißt normierter Normalenvektor und wird meistens mit $\vec{n}_0$ bezeichnet.
Möglichkeit 3: Ablesen an Koordinatenform
Wenn die Ebenengleichung in Koordinatenform vorliegt, habt ihr die Möglichkeit, den Normalenvektor direkt abzulesen. Die Koordinaten des Normalenvektors sind die Zahlen vor $x_1$, $x_2$ und $x_3$. Wenn in der Ebenengleichung z.B. kein $x_3$ vorkommt, ist dieser Eintrag beim Normalenvektor eine Null.
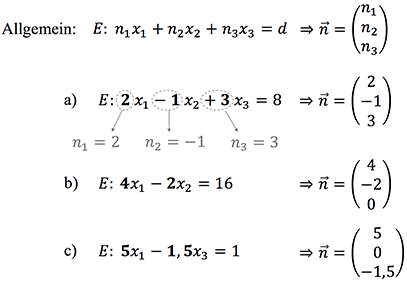
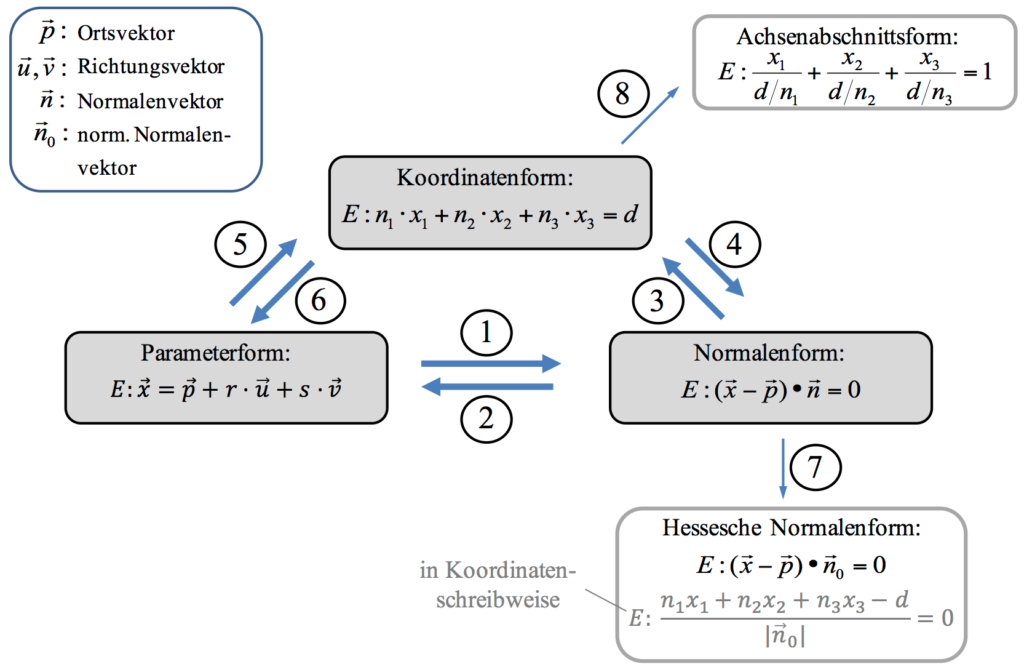
Umwandeln von Ebenengleichungen
Die folgende Abbildung gibt einen Überblick über das Umwandeln von Ebenengleichungen. Für jede Umwandlung werden wir gemäß der Nummerierung 1-8 ein Beispiel zeigen, damit keine Fragen mehr offen bleiben. Wozu müssen wir das können? Entweder weil das in der Aufgabe gefordert wird, oder weil eine andere Form der Ebene eine bestimmte Rechnung vereinfacht.
1,99€
Beispiel zu 1:
Gegeben sei die Ebene in Parameterform
\begin{align*}
E: \vec{x}=\begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ -1 \\ 7 \end{pmatrix} +t \cdot \begin{pmatrix} 3 \\ -1 \\ 6 \end{pmatrix}, \notag
\end{align*}
welche wir in Normalenform umwandeln möchten. Vorgehensweise:
- Normalenvektor $\vec{n}$ berechnen (= Kreuzprodukt der Richtungsvektoren)\begin{align*}
\vec{n}=\begin{pmatrix} 1 \\ -1 \\ 7 \end{pmatrix} \times \begin{pmatrix} 3 \\ -1 \\ 6 \end{pmatrix} = \begin{pmatrix} 1 \\ 15 \\ 2 \end{pmatrix} \notag
\end{align*} - Ortsvektor $\vec{p}=(2\ 1\ 1)^T$ von Parameterform übernehmen
- $\vec{n}$ und $\vec{a}$ in Normalenform einsetzen\begin{align*}
E: \left( \vec{x}- \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} \right) \bullet \begin{pmatrix} 1 \\ 15 \\ 2 \end{pmatrix}=0 \notag
\end{align*}
Beispiel zu 2:
Gegeben sei die Ebene in Normalenform
\begin{align*}
E: \left( \vec{x}- \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} \right) \bullet \begin{pmatrix} 1 \\ 15 \\ 2 \end{pmatrix} = 0\notag
\end{align*}
welche wir in Parameterform umwandeln möchten. Vorgehensweise
1. Ortsvektor $\vec{p}=(2\ 1\ 1)^T$ von Normalenform übernehmen:
\begin{align*}
E: \vec{x}=\begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + s \cdot \vec{u} + t \cdot \vec{v} \notag
\end{align*}
2. Suche nach zwei Richtungsvektoren $\vec{u}$ und $\vec{v}$, die senkrecht zum Normalenvektor $\vec{n}=(n_1 \ n_2 \ n_3)^T$ stehen. Es muss also gelten: $\vec{n} \bullet \vec{u} =0$ und $\vec{n} \bullet \vec{v} =0$.
Wähle
\begin{align*}
\vec{u} = \begin{pmatrix} 0 \\ -n_3 \\ n_2 \end{pmatrix} \quad \textrm{und} \quad \vec{v} = \begin{pmatrix} n_2 \\ -n_1 \\ 0 \end{pmatrix}
\end{align*}
In unserem Beispiel:
\begin{align*}
\vec{u} = \begin{pmatrix} 0 \\ -2 \\ 15 \end{pmatrix} \quad \textrm{und} \quad \vec{v} = \begin{pmatrix} 15 \\ -1 \\ 0 \end{pmatrix}
\end{align*}
Zur Kontrolle:
\begin{align*}
\vec{n} \bullet \vec{u} &= \begin{pmatrix} 1 \\ 15 \\ 2 \end{pmatrix} \bullet \begin{pmatrix} 0 \\ -2 \\ 15 \end{pmatrix} = 1\cdot 0 + 15 \cdot (-2) + 2 \cdot 15 = 0 \quad \\ \vec{n} \bullet \vec{v} &= \begin{pmatrix} 1 \\ 15 \\ 2 \end{pmatrix} \bullet \begin{pmatrix} 15 \\ -1 \\ 0 \end{pmatrix} = 1\cdot 15 + 15 \cdot (-1) + 2 \cdot 0 = 0 \quad
\end{align*}
3. Daraus folgt unsere Ebene in Parameterform
\begin{align*}
E: \vec{x}=
\begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ -2 \\ 15 \end{pmatrix} +t \cdot \begin{pmatrix} 15 \\ -1\\ 0 \end{pmatrix}. \notag
\end{align*}
Beispiel zu 3:
Gegeben sei die Ebene in Normalenform
\begin{align*}
E: \left( \vec{x}- \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} \right) \bullet \begin{pmatrix} 1 \\ 15 \\ 2 \end{pmatrix} = 0 \notag
\end{align*}
welche wir in Koordinatenform umwandeln möchten. Vorgehensweise: Ausmultiplizieren (Distributivgesetz), um auf den Ansatz $\vec{x}\bullet \vec{p}=\vec{n} \bullet \vec{p}$ zu kommen.
\begin{align*}
& \quad & \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \bullet \begin{pmatrix} 1 \\ 15 \\ 2 \end{pmatrix} – \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} \bullet \begin{pmatrix} 1 \\ 15 \\ 2 \end{pmatrix} \ & =0 \\
& \Leftrightarrow \quad & \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \bullet \begin{pmatrix} 1 \\ 15 \\ 2 \end{pmatrix} \ &= \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} \bullet \begin{pmatrix} 1 \\ 15 \\ 2 \end{pmatrix} \\
& \Leftrightarrow \quad & 1\cdot x_1+15\cdot x_2+2\cdot x_3 \ &= 2 \cdot 1 + 1 \cdot 15 + 1 \cdot 2 \\
& \Leftrightarrow \quad & 1\cdot x_1+15\cdot x_2+2\cdot x_3 \ &= 19
\end{align*}
Beispiel zu 4:
Gegeben sei die Ebene in Koordinatenform
\begin{align*}
1\cdot x_1+15\cdot x_2+2\cdot x_3 &= 19 \notag
\end{align*}
welche wir in Normalenform umwandeln möchten.Vorgehensweise:
- Normalenvektor anhand der Vorfaktoren ablesen: $\vec{n}=(1\ 15 \ 2)^T$
- Ortsvektor $\vec{p}$ finden. Dafür wählen wir zwei Variablen frei ($x_2=x_3=0$) und bestimmen die Übrige $x_1$:\begin{align*}\Rightarrow \ x_1 + 15 \cdot 0 + 2 \cdot0 &= 19 \notag \\x_1 &=19 \notag\end{align*}
- Normalenform aufstellen:\begin{align*}
E: \left( \vec{x}- \begin{pmatrix} 19 \\ 0 \\ 0 \end{pmatrix} \right) \bullet \begin{pmatrix} 1 \\ 15 \\ 2 \end{pmatrix} = 0\notag
\end{align*}
Beispiel zu 5:
Gegeben sei die Ebene in Parameterform
\begin{align*}
E: \vec{x}=\begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ -1 \\ 7 \end{pmatrix} +s \cdot \begin{pmatrix} 3 \\ -1 \\ 6 \end{pmatrix} \quad r,s \in \mathbb{R},
\end{align*}
welche wir in Koordinatenform umwandeln möchten.
Möglichkeit 1:
LGS aus Parameterform aufstellen und $r,\ s$ eliminieren.
\begin{align*}
\begin{array}{rccccccc}
\textrm{I} & x_1 & = & 2 & + & r & + & 3s \\
\textrm{II} & x_2 & = & 1 & – & r & – & s \\
\textrm{III} & x_3 & = & 1 & + & 7r &+ & 6s
\end{array}
\quad \textrm{aus III+7II und II+I:} \quad
\begin{array}{rccccccc}
\textrm{IV} & x_1 & + & x_2 & = & 3 & + & 2s \\
\textrm{V} & 7x_2 & + & x_3 & = & 8 & – & s
\end{array}
\end{align*}
Aus $2\textrm{V}+ \textrm{IV}$ folgt dann die gesuchte Koordinatenform:
\begin{align*}
x_1 + 15x_2 + 2x_3 = 19
\end{align*}
Möglichkeit 2:
Umweg über Normalenform. Ansatz:
\begin{align*}
(\vec{x}-\vec{p})\bullet \vec{n} = 0 \quad \Leftrightarrow \quad \vec{x} \bullet \vec{n}=\vec{p} \bullet \vec{n}
\end{align*}
mit $\vec{n}=\vec{u} \times \vec{v} = ( 1 \ 15 \ 2)^T$ folgt für die Koordinatenform
\begin{align*}
\begin{pmatrix}
x_1 \\ x_2 \\ x_3
\end{pmatrix} \bullet \begin{pmatrix}
1 \\ 15 \\ 2
\end{pmatrix} = \begin{pmatrix}
2 \\1 \\ 1
\end{pmatrix} \bullet \begin{pmatrix}
1 \\ 15 \\ 2
\end{pmatrix} \quad \Rightarrow \quad x_1 + 15x_2 + 2x_3 = 19
\end{align*}
Beispiel zu 6:
Gegeben ist die Ebene in Koordinatenform mit $2x_1 + 4x_2+3x_3=12$, welche wir in Paramaterform umwandeln möchten.
Möglichkeit 1:
Spurpunkte bzw. Achsenabschnittsform.
Aus
\begin{align*}
2x_1 + 4x_2+3x_3=12 \quad \textrm{auf AF bringen:} \quad
\frac{x_1}{6} + \frac{x_2}{3} + \frac{x_3}{4}=1
\end{align*}
können die Spurpunkte $S_1(6|0|0), \ S_2(0|3|0)$ und $S_3(0|0|4)$
abgelesen werden. Die Vokabel: Ebene aus drei Punkten aufstellen bringt die gesuchte Parameterform
\begin{align*}
E: \ \vec{x} = \underbrace{\begin{pmatrix} 6 \\ 0 \\ 0 \end{pmatrix}}_{\overrightarrow{0S_1}} + r \cdot \underbrace{\begin{pmatrix} -6 \\ 3 \\ 0 \end{pmatrix}}_{\overrightarrow{S_1S_2}} + s \cdot \underbrace{\begin{pmatrix} -6 \\ 0 \\ 4 \end{pmatrix}}_{\overrightarrow{S_1S_3}} \quad r,s \in \mathbb{R}.
\end{align*}
Möglichkeit 2:
Zwei Koordinaten durch Parameter $r$ und $s$ ersetzen.
\begin{align*}
\begin{array}{cccc}
\textrm{Sei} & x_1 &=& r \\
\textrm{und}& x_2 &=& s
\end{array} \quad \textrm{in Koordinatenform:} \quad
2r + 4s + 3x_3 = 12
\end{align*}
Wenn wir die Gleichung nach $x_3$ umstellen erhalten wir
\begin{align*}
x_3 = 4 – \frac{2}{3}r – \frac{4}{3}s
\end{align*}
und damit die gesuchte Parametergleichung
\begin{align*}
E: \ \vec{x} = \begin{pmatrix}
& r & \\ & & s \\ 4 & – \frac{2}{3}r & – \frac{4}{3}s
\end{pmatrix} = \begin{pmatrix}
0 \\ 0 \\ 4
\end{pmatrix} + r \cdot \begin{pmatrix}
1 \\ 0 \\ -2/3
\end{pmatrix}+ s \cdot \begin{pmatrix}
0 \\ 1 \\ -4/3
\end{pmatrix} \quad r,s \in \mathbb{R}.
\end{align*}
Beispiel zu 7:
Gegeben sei die Ebene in Normalenform
\begin{align*}
E: \left( \vec{x}- \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} \right) \bullet \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} = 0, \notag
\end{align*}
welche wir in die Hessesche Normalenform umwandeln möchten.
Vorgehensweise:
1. Länge des Normalenvektors $\vec{n}$ ausrechnen
\begin{align*}
|\vec{n}|=\sqrt{n_1^2+n_2^2+n_3^2}=\sqrt{2^2+1^2+(-2)^2}=\sqrt{9}=3 \notag
\end{align*}
2. Normierten Normalenvektor $\vec{n}_0$ mit der Formel $\vec{n}_0=\vec{n}/|\vec{n}|$ bestimmen:
\begin{align*}
\vec{n}_0 = \frac{\vec{n}}{|\vec{n}|} = \begin{pmatrix} 2/3 \\ 1 / 3 \\ -2 /3 \end{pmatrix} \notag
\end{align*}
3. In Hessesche Normalenform einsetzen:
\begin{align*}
E: \left( \vec{x}- \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} \right) \bullet \begin{pmatrix} 2/3 \\ 1 / 3 \\ -2 /3 \end{pmatrix} = 0\notag
\end{align*}
Beispiel zu 8:
Gegeben sei die Ebene in Koordinatenform
\begin{align*}
1\cdot x_1+15\cdot x_2+2\cdot x_3 &= 19 \notag
\end{align*}
welche wir in die Achsenabschnittsform umwandeln möchten. Dafür muss auf der rechten Seite des Gleichheitszeichens eine 1 stehen.
\begin{align*}
1\cdot x_1+15\cdot x_2+2\cdot x_3 &= 19 \quad |:19 \notag \\
\Leftrightarrow \quad \frac{x_1}{\frac{19}{1}}+ \frac{x_2}{\frac{19}{15}} +\frac{x_3}{\frac{19}{2}} &= 1 \notag
\end{align*}
Punktprobe Ebene
Beispiel mit Parameterform
Liegt der Punkt $P(1|2|4)$ auf der Ebene mit der Parameterform
\begin{align*}
E: \vec{x} = \left( \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right)
+ r \cdot \left( \begin{array}{c} 2 \\ 1 \\ 4 \end{array} \right)
+ s \cdot \left( \begin{array}{c} 3 \\ 1 \\ 5 \end{array} \right) \notag
\end{align*}
Hierfür muss müssen die Koordinaten der einzelnen Komponenten von $\vec{x}$, also $x_1,x_2,x_3$ durch die Koordinaten des Punktes $P$ ersetzt werden. Man erhält ein LGS mit 3 Gleichungen, welches nach $r$ und $s$ gelöst werden muss. Zur Bestimmung von 2 Unbekannten benötigt man nur 2 Gleichungen. Die dritte Gleichung dient somit der Kontrolle und muss wahr sein, wenn der Punkt auf der Ebene liegt.
Beispiel mit Koordinatenform
Liegt der Punkt $R(2|1|11)$ auf der Ebene mit der Koordinatengleichung $E: \ 3 x_1+7 x_2- x_3=2$?
Für $x_1$, $x_2$ und $x_3$ setzt man die Koordinaten des Punktes $R$ ein. $ 3 \cdot 2+7 \cdot 1 – 11=2$. Dies ist eine wahre Aussage, somit liegt der Punkt $R$ auf der Ebene.
Spurpunkte mit Koordinatenachsen
Ebene liegt in Koordinatenform vor
Spurpunkte einer Ebene sind die Schnittpunkte mit den Koordinatenachsen und die Spurgeraden sind die Verbindungsgeraden der Spurpunkte. Um möglichst einfach eine Aussage über Spurpunkte treffen zu können, sollte die Ebenengleichung in der sogenannten Achsenabschnittsform vorliegen. Hierfür müsst ihr die Koordinatenform einfach durch die Zahl teilen, bei der kein $x$ steht!
Aus der Koordinatenform $E: 3x + y + 2z = 6$ wird, wenn wir die Gleichung durch 6 teilen also die Achsenabschnittsform $E: \ (1/2)x + (1/6)y + (1/3)z = 1$.
Hier lassen sich die Achsenabschnitte leicht ablesen:
Der Schnittpunkt mit der $x$-Achse ist $S_x(2|0|0)$, welchen man erhält, wenn wir für $y$ und $z$ jeweils $0$ einsetzen. Es bleibt dann $(1/2)x = 1$ übrig! Diese Gleichung löst man nach $x$ auf und erhält $x=2$.
Einfacher: Immer die Zahl vor $x,y,z$ als Bruch hinschreiben und die Zahl im Nenner ist der gesuchte Spurpunkt mit der Achse! Analog hierzu erhalten wir für den Schnittpunkt mit der $y$-Achse $S_y(0|6|0)$ und der Schnittpunkt mit der $z$-Achse $S_z(0|0|3)$.
Ebene liegt in Parameterform vor
In diesem Abschnitt liegt die Ebene in Parameterform vor. Ausgehend von dieser Ebene sollen die Spurpunkte berechnet werden. Alternatives Vorgehen: Parameterform in die Achsenabschnittsform bringen (siehe Umwandlung von Ebenengleichungen). Hier wollen wir aber die Spurpunkte mit der Parameterform berechnen.
Bestimme die Spurpunkte der Ebene
\begin{align*}
E: \vec{x} = \left( \begin{array}{c} 1 \\ -1 \\ 3 \end{array} \right)
+ r \cdot \left( \begin{array}{c} 3 \\ 1 \\ 0 \end{array} \right)
+ s \cdot \left( \begin{array}{c} 4 \\ 2 \\ -1 \end{array} \right). \notag
\end{align*}
Zunächst stellen wir ein LGS mit $\vec{x}=(x_1, \ x_2, \ x_3)^T$ aus der Parameterform auf. Es folgt:
\begin{align*}
\textrm{I} \quad x_1 &= 1 + 3r+4s \\
\textrm{II} \quad x_2 &= -1 + 1r+2s \\
\textrm{III} \quad x_3 &= 3+ 0r-1s \\
\end{align*}
Für den Spurpunkt mit $x_1$-Achse setzen wir $x_2=x_3=0$ und erhalten
\begin{align*}
\textrm{II}^* \quad 0 &= -1 + r + 2s \\
\textrm{III}^* \quad 0 &= 3 – s
\end{align*}
Es liegt ein Gleichungssystem mit 2 Gleichungen und 2 Unbekannte vor, welches wir nach $r$ und $s$ mit den von uns bekannten Verfahren lösen. Glücklicherweise ist $s$ in $\textrm{III}^*$ die einzige Unbekannte, so dass wir direkt eine Lösung für $s$ erhalten und $s=3$ in $\textrm{II}^*$ einsetzen. Es folgt:
\begin{align*}
\Rightarrow \quad 0 &= -1 + r + 2\cdot 3 \\
\Leftrightarrow \quad 0 &= 5 + r \\
\Leftrightarrow \quad r &= -5 \\
\end{align*}
Jetzt nur noch die Werte von $r$ und $s$ in Gleichung $\textrm{II}$ einsetzen:
\begin{align*}
x_1=1+3\cdot (-5) +4 \cdot 3 = -2
\end{align*}
Der Spurpunkt mit der $x_1$-Achse lautet $S_1 (-2 | 0|0)$.
Die Berechnung der Spurpunkte mit der $x_2$– und $x_3$-Achse erfolgt analog. Ihr müsst dafür nur die anderen Koordinaten gleich Null setzen. Hier die Spurpunkte zur Kontrolle: $S_2 (0 | 2/3|0), \ S_3 (0 | 0|1)$.
Schau dir zur Vertiefung Daniels Lernvideo zum Thema Spurpunkte an!
