
Extremwertprobleme
Bei Extremwertprobleme (auch Optimierungsaufgaben oder Extremwertaufgaben genannt) geht es darum, Prozesse zu optimieren, minimalen oder maximalen Aufwand, Material oder Volumen zu erhalten.
Man sucht also eine Funktion, die unser Problem beschreibt und nur noch von einer Variablen abhängt. Wenn unsere Funktion von mehreren Variablen abhängt, müssen Variablen durch Nebenbedingungen so eliminiert werden, dass nur noch eine Variable vorliegt.
Wenn z.B. nach maximalen Volumen gefragt wird, ist die Hauptbedingung $V = \dots$. Soll nach minimaler Oberfläche gesucht werden ist die Hauptbedingung $O =\dots$.
Die Nebenbedingung enthält Informationen, wie zum Beispiel ein gegebenes Volumen, wenn die Oberfläche minimal bzw. maximal werden soll.
Vorgehensweise bei Extremwertaufgaben
- Hauptbedingung aufstellen: Was soll maximal/minimal werden?
- Rand- bzw. Nebenbedingung: Angabe im Text!
- Nebenbedingung nach einer Variablen umstellen und in Hauptbedingung einsetzen $\Rightarrow$ Zielfunktion.
- Zielfunktion auf Extremstellen untersuchen.
- Alle fehlenden Werte bestimmen. (Randwerte beachten!)
In diesem Themengebiet kommen zwei Aufgabentypen recht häufig vor: Körperaufgaben und umgangssprachlich Punkt auf Graph-Aufgaben.
Wir möchten an dieser Stelle zunächst auf den zweiten Aufgabentypen eingehen. Oft ist hier eine Funktion $f(x)$ vorgegeben, die sich in einem beliebigen Quadranten des Koordinatensystems befindet und in der sich ein Dreieck befindet, dessen Höhe und Breite abhängig von der Funktion $f$ ist. Genau so ein Fall wird im folgenden Beispiel behandelt.
Beispiel
Gegeben sei die Funktion $f(x)$ im ersten Quadranten. Welche Koordinaten muss der Punkt $P$ besitzen, damit der Flächeninhalt des grau schraffierten Dreiecks maximal ist?
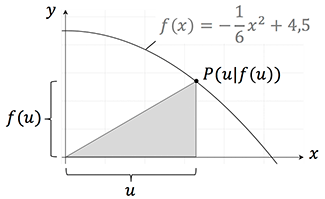
Hauptbedingung:
Unsere Hauptbedingung ist demnach der Flächeninhalt des Dreiecks:
\begin{align*}
A_\Delta=\frac{1}{2}\cdot g \cdot h
\end{align*}
Die Nebenbedingung ist in diesem Fall, dass der Punkt $P$ auf dem Funktionsgraphen liegen muss.
Das ist eine nützliche Information, denn so können wir die Grundseite $g$ und die Höhe $h$ in der Formel durch die Koordinaten von $P$ ersetzen:
Nebenbedingung:
\begin{align*}
g=u \ \ \textrm{und} \ \ h=f(u)=-\frac{1}{6}u^2+4,5
\end{align*}
Anschließend die Nebenbedingung in die Hauptbedingung einsetzen und wir erhalten die Zielfunktion:
\begin{align*}
A_\Delta(u) =\frac{1}{2}\cdot u \cdot\left( -\frac{1}{6}u^2+4,5 \right) =-\frac{1}{12}u^3+2,25 u
\end{align*}
Unsere Zielfunktion ist nur noch abhängig von der Unbekannten $u$. Wir untersuchen die Funktion nun auf Extremstellen.
Die notwendige Bedingung:
\begin{align*}
A’_\Delta(u) = -\frac{1}{4} u^2+2,25=0
\end{align*}
liefert die beiden möglichen Extremstellen $u_1=3$ und $u_2=-3$.
Da wir uns laut Aufgabentext im ersten Quadranten befinden haben wir nur die Lösung $u_1=3$.
Die Prüfung, ob wirklich ein Maximum vorliegt, wird mit der zweiten Ableitung gemacht und liefert $A“_\Delta(u_1=3)=-3/2<0$.
Für $u_1=3$ ist die Zielfunktion, also die Fläche des Dreiecks, wirklich maximal! Den meisten Lehrern reicht dieser Nachweis aus und ihr müsst jetzt noch die restlichen Werte bestimmen, hier die $y$-Koordinate von $P$: $f(3)=3$. Damit lautet der Punkt, der zur maximalen Fläche des Dreiecks führt $P(3|3)$.
Ab und zu wird noch der Nachweis gefordert, ob es sich tatsächlich um ein globales Maximum handelt. Um das zu prüfen, schauen wir uns das Verhalten der Funktion $A(u)$ an den Randwerten an. Doch was sind unsere Randwerte? Da wir uns laut Aufgabenstellung im ersten Quadranten befinden, ist der zulässige Definitionsbereich zwischen 0 und der Nullstelle der Funktion $f(x)$, also: $D = [0; 5{,}2]$. An den Rändern gilt $\lim_{u \to 0} A(u)=\lim_{u \to 5{,}2} A(u) = 0 $. Da $A(u)$ in $D = [0; 5{,}2]$ differenzierbar ist, gibt es in $D $ außer bei $u = 3$ kein weiteres Maximum.
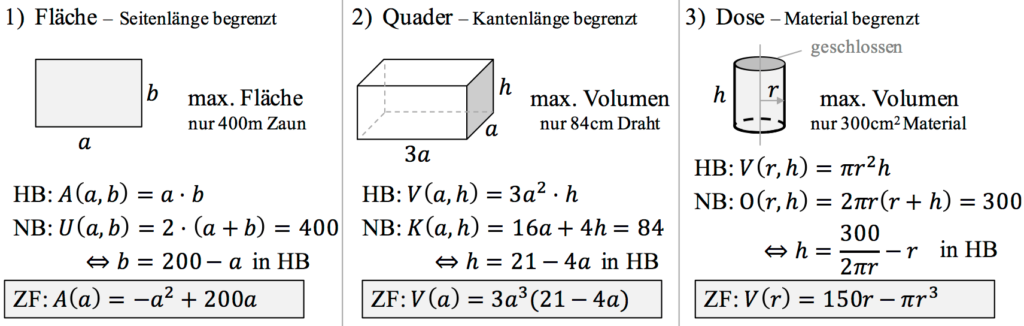
In der folgenden Abbildung findet ihr weitere typische Beispiele zu Extremwertaufgaben mit den dazugehörigen Zielfunktionen.
Die größte Schwierigkeit ist in der Regel, die Zielfunktion zu bestimmen. Diese Funktionen dann auf Extremstellen zu untersuchen, ist dann nicht mehr das Problem.
Hier eine vollständige Playlist mit Lernvideos zum Thema Extremwertprobleme.
