
Funktionen Grundlagen
Auf dieser Seite zum Thema „Grundlagen von Funktionen“ findest du Erklärungen zu folgenden Themen:
Inhaltsverzeichnis
- Lineare Funktion
- Quadratische Funktionen
- Polynomfunktion
- Wurzelfunktion
- Betragsfunktion
- Exponentialfunktion
- Logarithmusfunktion
- Manipulation von Grundfunktionen
- Umkehrfunktion
- Was ist in der Funktion gegeben?
Lineare Funktion
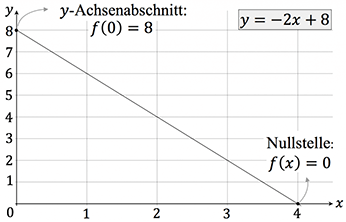
Die allgemeine Form für eine lineare Funktion lautet:
\begin{align*}
y=m \cdot x + b \quad \textrm{mit} \quad m=\frac{y_2-y_1}{x_2-x_1}
\end{align*}
Um die Steigung $m$ zu bestimmen brauchen wir zwei Punkte $P_1(x_1|y_1)$ und $P_2(x_2|y_2)$.
Hier findest du kostenlose Lernvideos zum Thema Lineare Funktionen.
Quadratische Funktionen
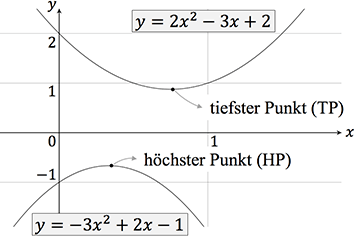
Die allgemeine Form für eine quadratische Funktion lautet:
\begin{align*}
y=ax^2+bx+c
\end{align*}
Die einfachste quadratische Funktion ist die Normalparabel mit $y=x^2$. Der höchste oder tiefste Punkt einer quadratischen Funktion wird auch Scheitelpunkt $S$ genannt. Die Scheitelpunktform lautet:
\begin{align*}
y=a\cdot (x-\boldsymbol{d})^2+e \quad \textrm{mit} \quad S(\boldsymbol{d}|e)
\end{align*}
Vollständige Playlist zum Thema Quadratische Funktionen
Polynomfunktion
Die allgemeine Form für eine Polynomfunktion (auch ganzrationale Funktion genannt)
3. Grades lautet:
$y=ax^3+bx^2+cx+d $
4. Grades lautet:
$y=ax^4+bx^3+cx^2+dx+e $
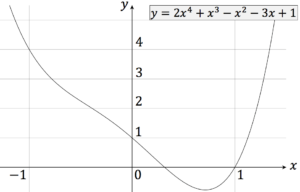
Grad $n$ beschreibt den höchsten Exponent für $x$ für $a\neq 0$. Es gibt maximal so viele Nullstellen, wie der Grad $n$ der Funktion ist.
Wurzelfunktion
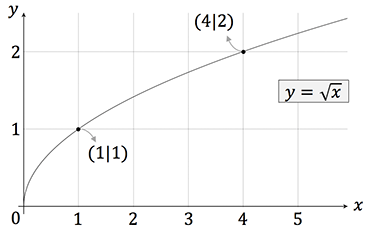
Die allgemeine Form einer Wurzelfunktion lautet:
\begin{align}
f(x)=\sqrt[n]{x} \ \text{für} \ x \geq 0 \notag
\end{align}
mit $n$ als Wurzelexponent. Sie besitzt die einzige Nullstelle bei $x=0$. Je größer $n$ ist, desto flacher verläuft der Graph ab $x=1$. Wenn $n$ gerade bzw. ungerade, ist $x\in [0, \infty)$ bzw. $x \in \mathbb{R}$.
Betragsfunktion
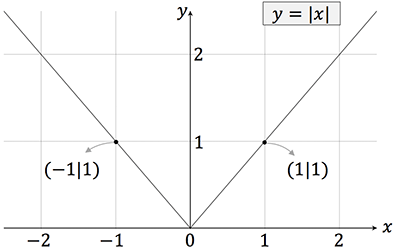
In der Mathematik ordnet die Betragsfunktion einer reellen Zahl ihren Abstand zur Null zu. Der sog. absolute Betrag, Absolutwert oder auch schlicht Betrag, ist immer eine nichtnegative Zahl, also größer oder gleich Null.
Schreibweisen: $f(x)=|x|$ oder $f(x)=abs(x)$.
Für eine beliebige reelle Zahl $x$ gilt:
\begin{align*}
|x| = \left\{ \begin{array}{ll} x&, \ x \geq 0 \\
-x&, \ x < 0 \end{array}\right. .
\end{align*}
Neu!
Exponentialfunktion
Eine Funktion heißt Exponentialfunktion (zur Basis a), wenn sie die Form
\begin{align}
f(x) = a^x = e^{x \cdot \ln(a)} \ \text{mit} \ x \in \mathbb{R}, a >0 \notag
\end{align}
aufweist, wobei $a$ eine beliebige positive Konstante bezeichnet. Falls $a = e$ ist, spricht man im Allgemeinen von der $e$-Funktion. Es handelt sich hierbei um die eulersche Zahl $e\approx 2,72$ – eine irrationale Zahl wie z.B. die Kreiszahl $\pi$. Sie verläuft oberhalb der $x$-Achse und besitzt keine Nullstelle.
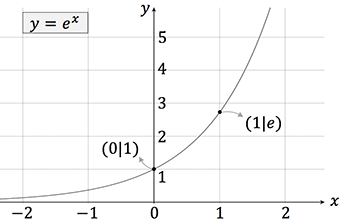
Die Form der Exponentialfunktion erinnert uns an einen Potenzausdruck, wobei die Rolle von Basis und Exponent vertauscht wird! Für den Fall, dass $a=e$ ist, gilt als Folge der Potenzgesetze für die $e$-Funktion: $e^0=1, \ e^1=e, \ e^x \cdot e^y = e^{x+y}$.
\begin{align*}
e^0=1, \ \ e^1=e, \ \ e^x \cdot e^y = e^{x+y}
\end{align*}
Logarithmusfunktion
Eine Funktion heißt Logarithmusfunktion (zur Basis $a$), wenn sie allgemein die Form
\begin{align*}
f(x) = \log_a(x), \ x \in (0,\infty)
\end{align*}
aufweist, wobei $a$ eine beliebige positive Konstante bezeichnet.
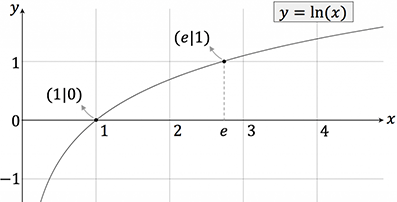
In den speziellen Fällen $a = e$ und $a = 10$ spricht man von
- $f(x)= \ln(x)$, als „natürlichen Logarithmus“ und
- $f(x) = \log(x)$, als „dekadischen Logarithmus“.
In der Regel rechnen wir aber mit dem natürlichen Logarithmus. Falls aber mal der Fall auftreten sollte, dass kein natürlicher Logarithmus vorliegt, kann dieser mit einfachen Mitteln wie folgt umgeschrieben werden:
\begin{align*}
log_a(x)=\frac{\ln(x)}{\ln(a)}
\end{align*}
Ein weiterer nützlicher Zusammenhang ist
\begin{align*}
e^{\ln(x)}=x \ \textrm{bzw.} \ \ln(e^x)=x,
\end{align*}
der im Bereich „Lösen von Gleichungen“ äußerst wichtig ist.
Logarithmengesetze
\begin{align*}
&\ln(ab)=\ln(a)+\ln(b) \\
&\ln(\frac{a}{b})=\ln(a)-\ln(b) \\
&\ln(a^b)=b\cdot \ln(a)
\end{align*}
Manipulation von Grundfunktionen
Auch Graphentransformation genannt. Idee: Aus dem Graphen einer gegebenen Funktion $f(x)$ mit dem Definitionsbereich $D$ und dem Wertebereich $W$ sollen die Graphen „neuer“ Funktionen $g(x)$ mit dem Definitionsbereich $D_g$ und dem Wertebereich $W_g$ durch einfache Operationen gewonnen werden.
Hier ist eine Übersichtstabelle, die die Manipulationen an Funktionen und die Wirkung auf den Graphen, den Definitionsbereich und den Wertebereich beschreibt. „Wirkung“ soll heißen: Bildet man den Term $g(x)$ wie beschrieben, so entsteht der Graph von $g$ aus dem Graphen von $f$ durch…
$
\begin{array}{c|c|c|c}
g(x)= & D_g= & W_g= & \text{Wirkung auf den Graphen} \\
\hline \hline
f(x)+a, \ a \in \mathbb{R} & D & a+W & \text{Verschiebung vertikal um a} \\
\hline
f(x+a), \ a \in \mathbb{R} & -a+D & W & \text{Verschiebung horizontal um -a} \\
\hline
c\cdot f(x), \ c>0 & D & c \cdot W & c>1: \text{Streckung, 0<c<1: Stauchung} \\
\hline
f(c\cdot x), \ c>0 & \frac{1}{c}\cdot D & W & c>1: \text{Stauchung}, 0<c<1: Streckung \\
\hline
-f(x) & D & -W & \text{Spiegelung an y-Achse} \\
\hline
-f(x) & D_f & -W_f & \text{Spiegelung an x-Achse}
\end{array}
$
Änderung innerhalb der Funktion, z.B. $f(x-a)$ $\stackrel{\wedge}{=}$ Horizontale Manipulation
- Definitionsbereich ändert sich
- Wertebereich bleibt gleich
Änderung außerhalb der Funktion, z.B. $f(x)+a$ $\stackrel{\wedge}{=}$ Vertikale Manipulation
- Definitionsbereich bleibt gleich
- Wertebereich ändert sich
Im Folgenden werden wir die am häufigsten vorkommenden Manipulationen bzw. Transformationen anhand eines Beispiels vorstellen. Als Ausgangsfunktion dient die Normalparabel
\begin{align*}
f(x) = x^2, \quad x \in \mathbb{R}.
\end{align*}
Verschiebung in x-Richtung
Die Verschiebung in $x$-Richtung können wir in unserer Funktionsgleichung leicht berücksichtigen. Dazu werfen wir zunächst einen Blick auf die Graphen im folgenden Koordinatensystem.
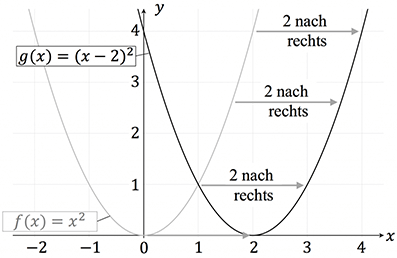
Der Scheitelpunkt dieser Parabel und alle anderen Punkte wurden ausgehend von der Normalparabel um 2 Einheiten nach rechts verschoben. Wenn wir einen Blick auf die Funktionsgleichung werfen, sehen wir, dass sie wie folgt lautet:
\begin{align*}
g(x) = (x-2)^2
\end{align*}
Eine Verschiebung in $x$-Richtung kann man immer daran erkennen, dass der Wert, um welchen die Funktion verschoben wurde, mit umgekehrten Vorzeichen in der Klammer auftaucht.
Dazu wollen wir uns noch eine Parabel angucken, die nach links verschoben werden soll.
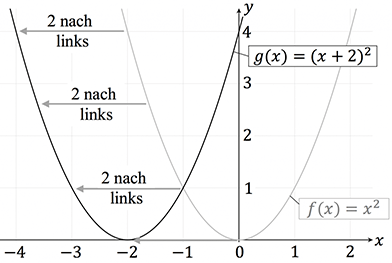
Die Funktionsgleichung dieser Parabel lautet:
\begin{align*}
g(x) = (x+2)^2
\end{align*}
Die Parabel wurde um 2 Einheiten nach links verschoben. Ganz allgemein können wir also sagen: Die Funktion $f(x-a)$ verschiebt sich um $+a$ entlang der $x$-Achse.
Verschiebung in y-Richtung
Die Verschiebung in $y$-Richtung erkennen wir daran, dass der Wert, um den die Funktion in $y$-Richtung verschoben wurde, ohne Klammer mit dem korrekten Vorzeichen angehängt wird.
Ausgehend der Normalparabel betrachten wir die folgenden Funktionen:
\begin{align*}
g(x)=x^2-2 \quad \quad \textrm{und} \quad \quad h(x)=x^2+2
\end{align*}
Dazu gucken wir uns die das nachfolgende Koordinatensystem an.
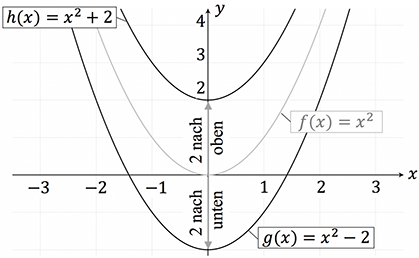
Das $-2$ in der Gleichung von $g(x)$ bedeutet, dass die Normalparabel um 2 Einheiten nach unten verschoben wird. Analog folgt durch das $+2$ eine Verschiebung um 2 Einheiten nach oben. Allgemein können wir sagen: Die Funktion $f(x)+a$ verschiebt sich um $+a$ entlang der $y$-Achse.
Natürlich ist es auch möglich, sowohl eine Verschiebung in $x$-Richtung als auch eine Verschiebung in $y$-Richtung gleichzeitig durchzuführen. Dazu betrachten wir die Parabel in der folgenden Abbildung.
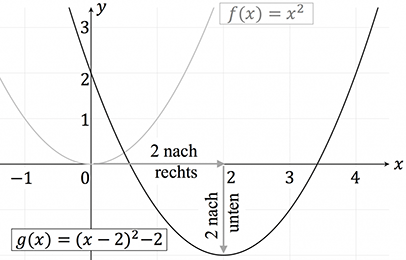
Die Funktionsgleichung lautet:
\begin{align*}
g(x)=(x-2)^2-2
\end{align*}
In der Klammer erkennen wir die Verschiebung um 2 Einheiten nach rechts und hinter der Klammer erkennen wir die Verschiebung um 2 Einheiten nach unten. Eine Funktionsgleichung in der Form wird Scheitelpunktform genannt. Dadurch ist es direkt möglich die Koordinaten des Scheitelpunktes abzulesen. In unserem Fall also $S(2|-2)$.
Neu!
Stauchung und Streckung
Wenn wir eine Funktion strecken oder stauchen wollen, müssen wir die Funktion mit einem Faktor $c$ multiplizieren. In unserem Beispiel mit der Normalparabel wird aus $f(x)=x^2$ dann $g(x)=c\cdot f(x)=c \cdot x^2$. Dabei gilt für den Faktor $c$, wenn
\begin{align*}
c>1 \quad &\Rightarrow \ &\textrm{Streckung} \\
0<c<1 \quad & \Rightarrow \ & \textrm{Stauchung}
\end{align*}
Der Faktor $c$ gibt also an, ob es sich um eine Streckung oder um eine Stauchung handelt und befindet sich entweder direkt vor dem $x^2$ oder, falls unsere Funktionsgleichung in der Scheitelpunktform vorliegen sollte, direkt vor der Klammer.
Die Normalparabel $x^2$ hat den Faktor $c=1$. Diesen schreiben wir aus Gründen der mathematischen Faulheit aber nicht hin. Die Normalparabel ist also weder gestreckt noch gestaucht.
Eine gestreckte Parabel könnte die Gleichung
\begin{align*}
g(x)=2\cdot x^2
\end{align*}
haben.
Da der Vorfaktor $c$ größer als 1 ist, wird die Parabel gestreckt. Der Graph verläuft wesentlich schmaler als die Normalparabel. Jeder $y$-Wert wird mit dem Faktor $c=2$ multipliziert.
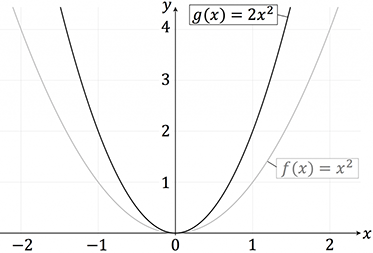
Wenn der Faktor $c$ zwischen 0 und 1 liegt, wird die Funktion gestaucht.Die Funktion
\begin{align*}
g(x)&=0,5\cdot x^2
\end{align*}
beschreibt eine gestauchte Normalparabel, welche breiter ist als die Normalparabel $f(x)=x^2$. Jeder $y$-Wert wird mit dem Faktor $c=0,5$ multipliziert.
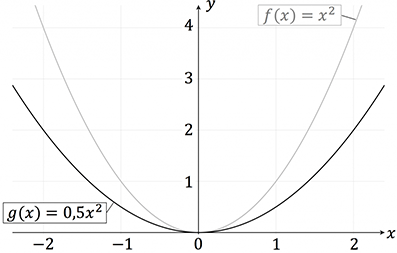
Ganz allgemein können wir sagen: Die Funktion $c\cdot f(x)$ wird gestreckt, wenn $c>1$ und gestaucht, wenn $0<c<1$ ist.
Es kann zwischen vertikaler und horizontaler Stauchung bzw. Streckung unterschieden werden. Das was wir gerade kennengelernt haben, war die vertikale Stauchung und Streckung.
Die horizontale können wir allgemein wie folgt formulieren: Die Funktion $f(c\cdot x)$ wird gestreckt, wenn $0<c<1$ und gestaucht, wenn $c>1$ ist.
Neu!
Spiegelung
Wir erkennen eine an der $x$-Achse gespiegelte Funktion daran, dass ein Minus vor der Funktion steht. In unserem Beispiel lautet die an der $x$-Achse gespiegelte Normalparabel
\begin{align*}
g(x)=-f(x)=-x^2.
\end{align*}
Der Graph von $g$ und $f$ ist in der nachfolgenden Abbildung dargestellt. Jeder $y$-Wert wird mit $(-1)$ multipliziert.
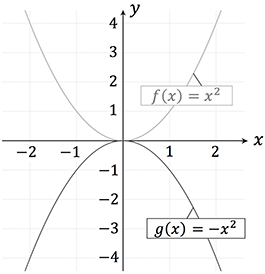
Wie bei der Stauchung und Streckung können wir hier eine Unterteilung in eine vertikale und horizontale Spiegelung vornehmen. Allerdings ist die horizontale Spiegelung, also die Spiegelung an der $y$-Achse, hier nur bedingt möglich. Denn die gespiegelte Funktion $g(x)=f(-x)=(-x)^2=x^2=f(x)$ ist nichts anderes als die Normalparabel selbst. Warum? Weil das Quadrat aus dem Minus ein Plus macht.
Betrachten wir die Funktion $f(x)=x^3$ und möchten diese an der $y$-Achse spiegeln, lautet die transformierte Funktion
\begin{align*}
g(x)=f(-x)=(-x)^3=-x^3
\end{align*}
Jeder $x$-Wert wird mit $(-1)$ multipliziert. Da die Funktion punktsymmetrisch ist, ist die horizontale Spiegelung gleich der Vertikalen. Allgemein können wir sagen: Die Funktion $-f(x)$ bzw. $f(-x)$ wird an der $x$– bzw. $y$-Achse gespiegelt.
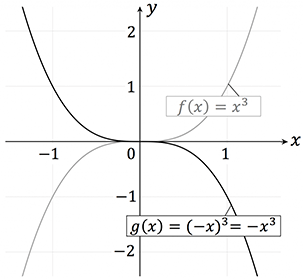
weiteres Beispiel (nicht so ausführlich) Im Folgenden werden wir für jede Operation aus der Tabelle eine kleine Beispielskizze angeben. Als Ausgangsfunktion dient die Funktion
\begin{align*}
f(x) = \sqrt{x}
\end{align*}
mit dem Definitionsbereich $x \in D:=[0;4]$ und dem Wertebereich $W=[0;2]$.
Für die Parameter $a$ und $c$ verwenden wir beispielhaft $a=5$ und $c=2$! Wir werden sehen, wie sich die Graphen der Funktionen ändern und geben zudem den neuen Definitions- und Wertebereich ($D_g$, $W_g$) an. Den Graphen der Ausgangsfunktion sehen wir in der nebenstehenden Abbildung.
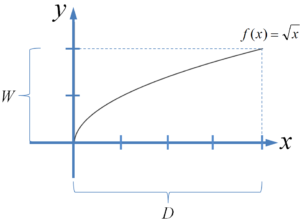
Horizontale Verschiebung: $g(x)=f(x+a)=f(x+5)=\sqrt{x+5}$
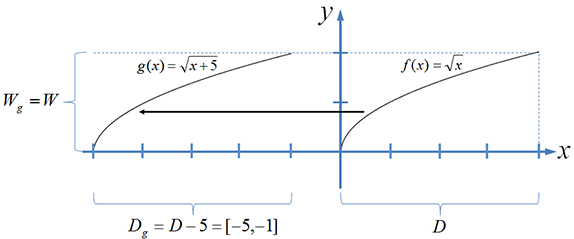
Horizontale Spiegelung: $g(x)=f(- x)=\sqrt{-x} $
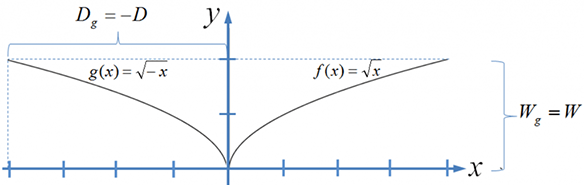
Horizontale Stauchung
$g(x)=f(c \cdot x)=f(2\cdot x)=\sqrt{2x}$
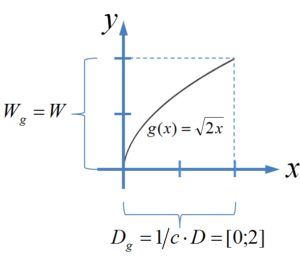
Neu!
Vertikale Streckung:
$g(x)=c\cdot f(x)=2\cdot f(x)=2 \cdot \sqrt{x}$
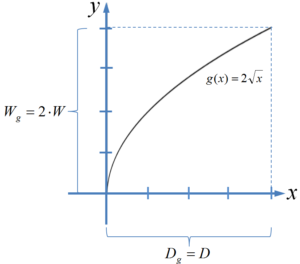
Vertikale Verschiebung:
$g(x)=f(x)+5 =\sqrt{x}+5 $
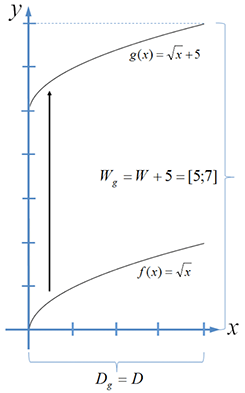
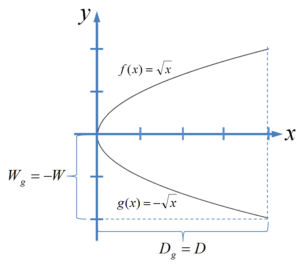
Vertikale Spiegelung:
$g(x)=- f(x)=- \sqrt{x}$
In Daniels Playlist zu Funktionen findest du weitere hilfreiche Videos.
Umkehrfunktion
Für eine Funktion $f(x)$ ist $f^{-1}(x)$ eine Umkehrfunktion, wenn für $y=f(x)$ gilt: $x=f^{-1}(y)$. Also wenn man in die Umkehrfunktion einen Funktionswert $y$ der Ausgangsfunktion einsetzt, so erhält man den dazugehörigen $x$-Wert.
Vorgehen:
- Funktion als $y = f(x)$ umschreiben und schrittweise nach $x$ lösen.
- Variablen $x$ und $y$ tauschen.
- Umkehrfunktion $f^{-1}(x)$ oder $\bar{f}(x)$ aufschreiben.
Eine Funktion ist umkehrbar, wenn jeder Funktionswert $y$ nur an einer einzigen Stelle $x \in D_f$ angenommen wird: $f(x_1) = f(x_2) \Rightarrow x_1 = x_2$.
Eine solche Funktion $f$ hat eine Umkehrfunktion $f^{-1}$, definiert durch $f^{-1}(y)=x$ für $y=f(x)$, also $f^{-1}\left(f(x) \right) = x$. In manchen Fällen muss man den Definitionsbereich einer Funktion einschränken, damit die so eingeschränkte Funktion umkehrbar ist.
Beispiele
a) Lineare Funktion: Bestimme die Umkehrfunktion von $f(x)=2x+1$.
Wir arbeiten das obige Vorgehen ab und lösen die Gleichung nach $x$ auf.
\begin{align*}
& \ & y \ & = 2x+1 \quad &&|-1 \\
& \Leftrightarrow \ & y-1 \ & = 2x \quad &&|:2 \\
& \Leftrightarrow \ & 0,5y-0,5 \ & =x \quad &&
\end{align*}
Das Tauschen von $x$ und $y$ zu $y = 0,5x-0,5 $ liefert die Umkehrfunktion
\begin{align*}
f^{-1}(x) = 0,5x-0,5.
\end{align*}
Grafische Darstellung der Funktion und ihrer Umkehrfunktion:
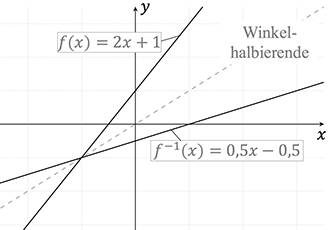
b) Quadratische Funktion: Bestimme die Umkehrfunktion von $f(x) = (x+2)^2 $.
Wir arbeiten das obige Vorgehen ab und lösen die Gleichung nach $x$ auf.
\begin{align*}
& \quad & y \ & = (x+2)^2 \quad &&|\sqrt{ } \\
& \Leftrightarrow \quad & \pm \sqrt{y} \ & =x+2 \quad &&|-2 \\
& \Leftrightarrow \quad & \pm \sqrt{y}-2 \ & =x \quad &&
\end{align*}
Das Tauschen von $x$ und $y$ zu $y = \pm \sqrt{x}-2$ liefert die Umkehrfunktionen
\begin{align*}
f^{-1}_1(x) &= \sqrt{x}-2 \ \textrm{und} \\ f^{-1}_2(x) &= -\sqrt{x}-2.
\end{align*}
Grafische Darstellung der Funktion und ihrer Umkehrfunktion:
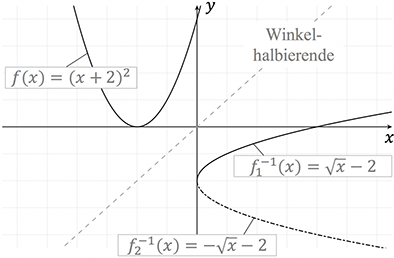
Bei einer quadratischen Funktion wie zum Beispiel $y = x^2$ tritt ein Problem auf. Hier liegt keine eindeutige Zuordnung vor, denn einem $y$-Wert sind zwei $x$-Werte zugeordnet. Es lässt sich dann für einen Teil eine Umkehrfunktion definieren, wie im Beispiel der Normalparabel mit $f^{-1}_1(x)=\sqrt{x}$ für den positiven Teil und $f^{-1}_2(x)=-\sqrt{x}$ für den negativen Teil.
Zur Vertiefung solltest du dir das Lernvideo von Daniel zum Thema Umkehrfunktionen anschauen!
Was ist in der Funktion gegeben?
In Anwendungsaufgaben müssen wir verstehen, was die Funktion überhaupt beschreibt. Oft geht es dabei um Füllbestände irgendwelcher Stauseen oder Geschwindigkeiten von Flugzeugen. Daher ist es sehr wichtig zu wissen, was z.B. die Ableitung der Geschwindigkeit im Sachzusammenhang bedeutet.
Die folgende Übersicht soll euch als Zusammenfassung dienen. Wenn in unserer Funktion für $f(t)$ folgendes angegeben ist, dann ist

Schau dir das Lernvideo von Daniels zum Thema Anwendung von Funktionen an!
Sieh dir zur Vertiefung Daniels Playlist zum Thema Funktionen an!

