
Funktionsschar
Das Thema Funktionsschar wird euch sicherlich in der Oberstufe vor dem Abitur begegnen. Damit ihr in Zukunft genau bescheid wisst, haben wir euch alles rund um das Thema Funktionsschar in diesem Artikel zusammengefasst.
Inhaltsverzeichnis
- Scharfunktion Grundlagen
- Fallunterschreidung
- Ableiten und Integrieren der Funktionsschar
- Ortskurve der Funktionsschar
Scharfunktion Grundlagen
Wenn man Berechnungen an- und mit Funktionsschar durchführen muss, dann ist das Erste was meist gefragt wird: Was soll denn der Buchstabe da, der nicht x ist?
Und wenn wir jetzt eine Kurvendiskussion einer solchen Funktionsschar durchführen, berechnen wir damit unendlich viele Kurvenuntersuchungen auf einmal, da wir im Nachhinein eine konkrete Zahl für unseren Parameter einsetzen können.
Ist die Funktion linear, spricht man auch von einer Geradenschar. Im Allgemeinen verändern die Parameter das Aussehen und die Form der Kurve auf eine Weise, die komplizierter als eine einfache lineare Transformation ist.
In der folgenden Abbildung sind für zwei Funktionsschar verschiedene Parameter eingesetzt worden.
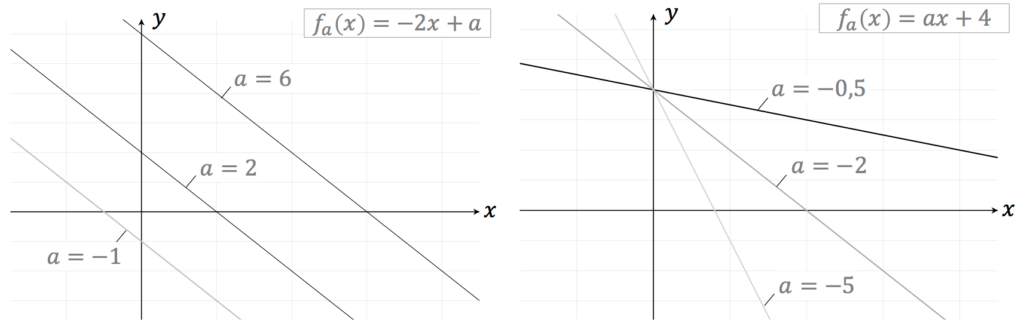
Beim Schreiben der Funktionsvorschrift wird der variable Parameter in den Index geschrieben, z.B.
\begin{align*}
f_a(x) = a x² – 2 a x+4 a.
\end{align*}
Beachtet: Der Parameter ist zu behandeln wie eine ganz gewöhnliche Zahl!
Neu!
Fallunterscheidung bei Funktionsschar
Eine Schwierigkeit beim Rechnen mit einer Funktionsschar taucht oft bei der Berechnung ihrer Nullstellen auf, vor allem wenn der Scharparameter „drin“ geblieben ist. In diesem Fall kommt dann die Fallunterscheidung zum Einsatz.
Warum müssen wir verschiedene Fälle betrachten? Ihr solltet immer im Hinterkopf haben, dass der Parameter verschiedene Werte annehmen kann. Nur Zahlen größer Null? Kann der Parameter Null sein oder sogar kleiner Null? Das sollte in der Regel im Aufgabentext vorgegeben sein.
Gegeben sei die Funktionsschar
\begin{align*}
f_a(x)=(a-1)x^3-4ax
\end{align*}
mit dem Parameter $a$. Wenn
- $a > 0$ bzw. $a \in \mathbb{R}^+$: keine Fallunterscheidung nötig
- $a \in \mathbb{R}$ oder $a \neq 0$: Parameter a kann auch negativ Werte annehmen! Hier ist eine Fallunterscheidung nötig.
Größtenteils läuft die Berechnung von Kurvenscharen auf genau so etwas hinaus.
Zum Beispiel sei folgende Funktionsschar gegeben:
\begin{align*}
f_a(x)=\frac{1}{x-a}
\end{align*}
Wenn
- x = a ist, dann wäre die Funktion nicht definiert, da dann der Nenner gleich Null ist und wir nicht durch Null teilen dürfen.
- x > a oder x < a ist, ist die Funktion definiert und wir können mit ihr arbeiten.
Auch bei der Berechnung von Extremstellen ist die Fallunterscheidung wichtig. Hier ein Beispiel bei der hinreichenden Bedingung von Extrema:
- $f_a“(…)=20a > 0$, wenn a > 0 TP
- $f_a“(…)=20a < 0$, wenn a < 0 HP
- $f_a“(…)=20a = 0$, wenn a = 0 SP
Funktionsschar – Ableiten und Integrieren mit Parameter
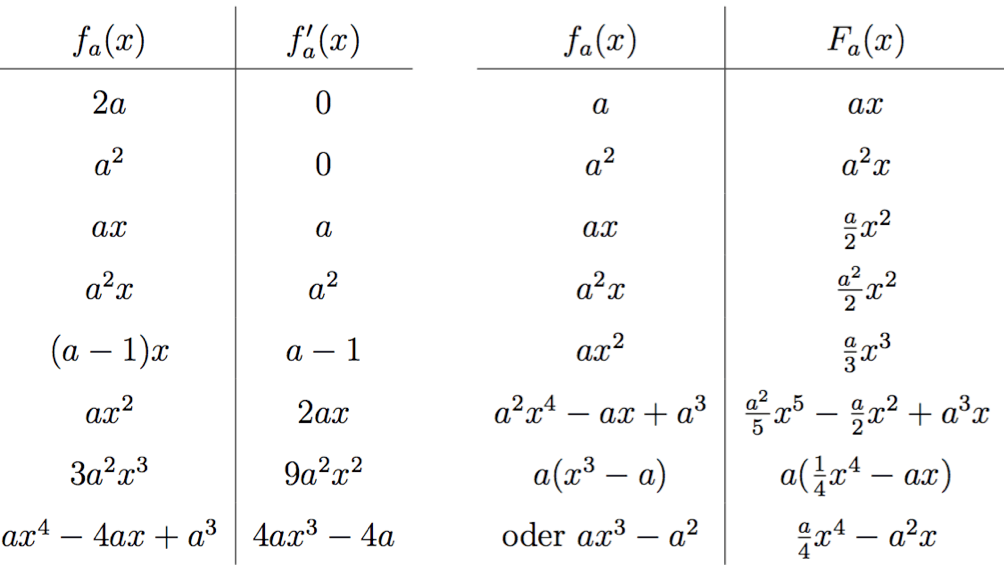
Daniel erklärt in seinem Lernvideo nochmals alles rund ums Thema Funktionsschar ableiten.
Ortskurve einer Funktionsschar
Als Ortskurve bezeichnet man eine Kurve, auf der alle Punkte einer gegebenen Funktionsschar liegen, die eine bestimmte Eigenschaft erfüllen. In einer Kurvendiskussion werden häufig die Ortskurven von Extrempunkten oder Wendepunkten der Graphen einer Funktionenschar gesucht.
Zur Berechnung der Ortskurve werden zunächst die Koordinaten der betreffenden Punkte (z.B. aller Tiefpunkte einer Funktionenschar) in Abhängigkeit vom jeweiligen Parameter (z.B. a oder k) bestimmt.
Vorgehensweise:
1. allgemeine Punkte P(x|y) mit bestimmter Eigenschaft, z.B. Extrem- oder Wendepunkte, in Abhängigkeit vom Parameter bestimmen
2. x-Wert nach Parameter umstellen und in y-Wert einsetzen
3. y-Wert ist die Ortskurve
Beispiel
Gegeben sei die Funktionsschar $f_a(x) = x^2 – ax, \ a \in \mathbb{R}.$
Bestimme die Ortskurve, auf der alle Extrempunkte der Funktion liegen.
Als erstes bestimmen wir die Extrempunkte in Abhängigkeit von a:
\begin{align*}
f’_a(x)=2x-a = 0 \Rightarrow x = \frac{a}{2}
\end{align*}
Es handelt sich um einen Tiefpunkt, da $f“_a(x)=2 > 0$ ist. Alle Tiefpunkte der Funktionsschar liegen bei $T(\frac{a}{2} | -\frac{a^2}{4})$.
Um die Ortskurve zu erhalten, müssen wir die x-Koordinate des allgemeinen Tiefpunktes nach dem Parameter umstellen. Es folgt:
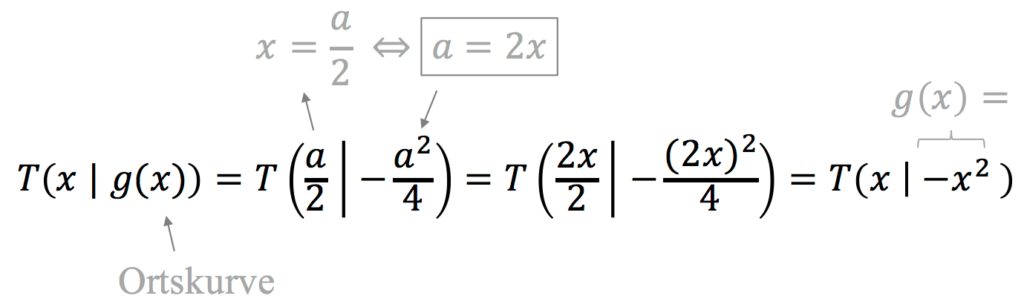
Damit lautet die Ortskurve $g(x)=-x^2$, die alle Tiefpunkte der Funktionenschar verbindet. Grafisch kann man sich die Ortskurve wiefolgt darstellen:
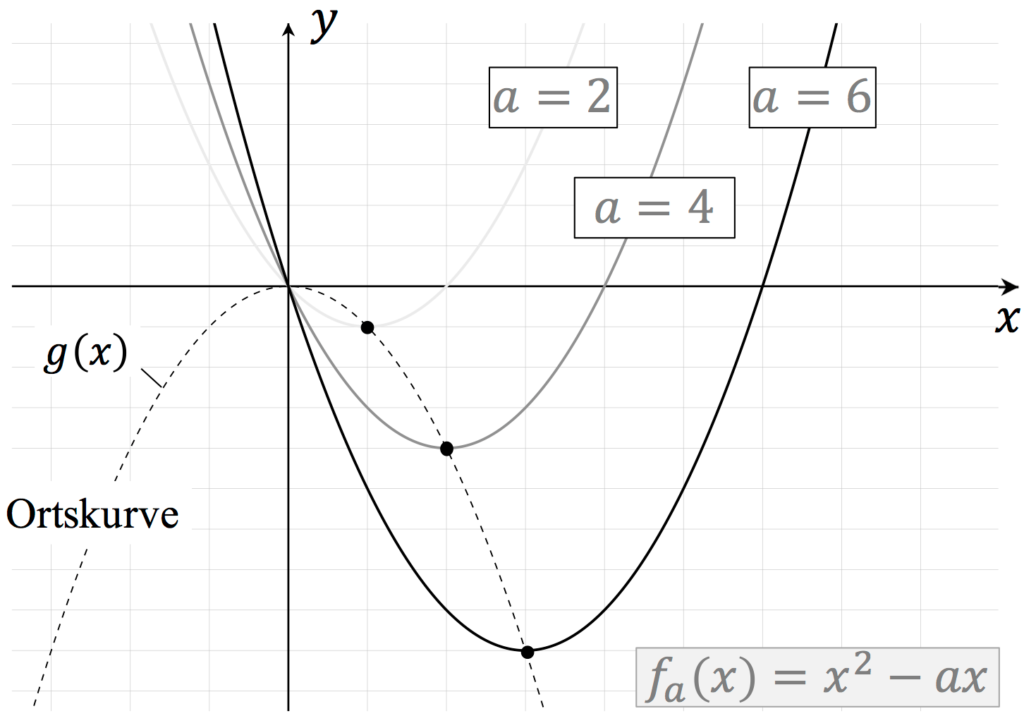
Vertiefe dein Wissen mit dem Lernvideo von Daniel zum Thema Ortskurve einer Funktionsschar

