
Geraden berechnen
Es gibt verschiedene Wege Geraden zu berechnen. Damit du in der Prüfung ganz genau weißt, wie du vorgehen musst, haben wir dir alle Arten in folgendem Artikel aufgeschrieben.
- Parameterform einer Geraden
- Punktprobe Gerade
- Spurpunkte von Gerade in Koordinatenebene
- Geschwindigkeitsaufgaben
1,99€
Parameterform einer Geraden
Die Gleichung einer Geraden $g$ durch die Punkte $A$ und $B$ mit den Ortsvektoren $\vec{a}$ und $\vec{b}$ lautet:
\begin{align*}
g:\vec{x} = \vec{a} + t \cdot \vec{u}, \quad t \in \mathbb{R}, \notag
\end{align*}
wobei $\vec{u} = \vec{b}-\vec{a}$ der Richtungsvektor zwischen den Punkten $A$ und $B$ sowie $t$ eine beliebige reelle Zahl, unser Parameter, ist.
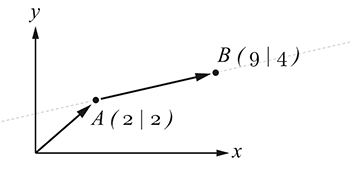
Gerade in der Ebene: $$g:\vec{x} = \left( \begin{array}{c} 2 \\ 2 \end{array} \right) + t \cdot \left( \begin{array}{c} 7 \\ 2 \end{array} \right) $$
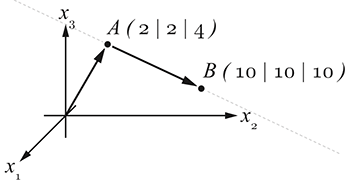
Gerade im Raum: $$g:\vec{x} = \left( \begin{array}{c} 2 \\ 2 \\ 4 \end{array} \right) + t \cdot \left( \begin{array}{c} 8 \\ 8 \\ 6 \end{array} \right)$$
Da diese Gleichung den Parameter $t$ enthält, spricht man von der Parameterform einer Geradengleichung. Durchläuft $t$ alle reellen Zahlen, erhält man jeden Punkt der Geraden $g$ (gestrichelte Linie). Der Vektor $\vec{a}$ heißt Ortsvektor (auch Stützvektor oder Pin), der Vektor $\vec{u}$ heißt Richtungsvektor.
1,99€
Vertiefe dein Wissen mit Daniels Lernvideo!
Punktprobe Gerade
Eine Punktprobe wird durchgeführt, indem man die Koordinaten des Punktes in die Gleichung der Punktmenge einsetzt. Erfüllt der Punkt die Gleichung, d.h. entsteht eine wahre Aussage, so liegt der Punkt in der Punktmenge. Entsteht eine falsche Aussage, so liegt der Punkt nicht in der Punktmenge.
Somit ist es möglich, am Ende einer Rechnung zu überprüfen, ob z. B. ein berechneter Schnittpunkt zweier Geraden tatsächlich auf beiden Geraden liegt.
BeispielLiegt der Punkt $Q(8|3|5)$ auf der Geraden $h$ mit der Parametergleichung?
\begin{align*}
h: \vec x = \begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix}, t \in \mathbb{R} \notag
\end{align*}
Für den Vektor $\vec x$ setzt man den Ortsvektor zu Punkt $Q$ ein und löst zeilenweise nach dem Parameter $t$ auf. Da sich in der ersten Zeile $t =2$ ergibt, gleichzeitig die zweite Zeile aber $t = -3$ liefert, gibt es einen Widerspruch. Somit liegt der Punkt $Q$ nicht auf der Geraden $h$.
Wenn wir für alle $t$’s den gleichen Wert berechnet hätten, wäre das eine wahre Aussage und der Punkt für auf der Geraden liegen.
Lass dir nochmal von Daniel die Punktprobe bei Geraden erklären.
Spurpunkte von Gerade in Koordinatenebene
Unter einem Spurpunkt versteht man den Schnittpunkt einer Geraden mit einer Koordinatenebene. Da es im dreidimensionalen Raum drei Koordinatenebenen gibt ($E_{23}$, $E_{13}$ und $E_{12}$), lassen sich drei Spurpunkte berechnen:
- $S_1$ ist der Schnittpunkt von Gerade und $x_2x_3$-Ebene
- $S_2$ ist der Schnittpunkt von Gerade und $x_1x_3$-Ebene
- $S_3$ ist der Schnittpunkt von Gerade und $x_1x_2$-Ebene
Vorgehensweise zur Berechnung von Spurpunkten $S_i$:
- $i$-te Koordinate der Geradengleichung gleich Null setzen und den dazugehörigen Parameter $t$ berechnen
- $t$ in die Geradengleichung einsetzen, um die Koordinaten des Spurpunktes zu erhalten
Beispiel
Gegeben sei die Gerade
\begin{align*}
g: \vec x = \left( \begin {array} {c} 1\\ -4\\ 4 \end {array} \right)
+ t \cdot \left( \begin {array} {c} 1\\ 2\\-1 \end {array} \right).
\end{align*}
Berechne den Spurpunkt $S_1$ der Geraden mit der $x_2x_3$-Ebene.
Hierfür arbeiten wir die Punkte der obigen Vorgehensweise ab. Als erstes $x_1=0$ in die erste Zeile der Geradengleichung einsetzen, um $t$ zu berechnen.
\begin{align*}
0=1+t\cdot 1 \quad \Rightarrow \quad t=-1 \notag
\end{align*}
Dann muss $t$ in die Geradengleichung eingesetzt werden, um den Spurpunkt zu berechnen.
\begin{align*}
S_1 = \left( \begin {array} {c} 1\\ -4\\ 4 \end {array} \right)
+(-1) \cdot \left( \begin {array} {c} 1\\ 2\\-1 \end {array} \right) = \left( \begin {array} {c} 0 \\ -6 \\ 5 \end {array} \right). \notag
\end{align*}
Der Spurpunkt mit der $x_2x_3$-Ebene hat demnach die Koordinaten $S_1=(0|-6|5)$.
Schau dir nochmals das Lernvideo zum Thema Spurkunkte an, um dein Wissen zu vertiefen!
Geschwindigkeitsaufgaben
Wir betrachten ein dreidimensionales Koordinatensystem und die Koordinatenachsen stellen die Richtungen Ost, Nord und senkrecht nach oben dar. Es gilt
\begin{align*}
\begin{pmatrix}
x_1 \\ x_2 \\ x_3
\end{pmatrix} =
\begin{pmatrix}
\textrm{Ost} \\ \textrm{Nord} \\ \textrm{Oben}
\end{pmatrix}. \notag
\end{align*}
Die Längeneinheit in allen drei Richtungen beträgt 1 km.
Gegeben sind vier Punkte im Raum:
\begin{align*}
A(5 | 9 | 8),\ B( 5 | 1 | 8), \ C( 13 | 33 | 10),\ D (19 | 27 | 9). \notag
\end{align*}
Die Geraden
\begin{align*}
g : \vec{x}= \vec{a}+t\cdot (\vec{b}-\vec{a}), \ t \in \mathbb{R} \notag \\
h : \vec{x}= \vec{c}+t\cdot (\vec{d}-\vec{c}), \ t \in \mathbb{R} \notag
\end{align*}
beschreiben kurzzeitig die Bahnen zweier Flugzeuge.
Wichtig:
Bei Geschwindigkeitsaufgaben muss beachtet werden, dass der Parameter (hier $t$) für die Zeit benutzt wird und bei beiden Gleichungen gleich ist.
Um 8.00 Uhr befand sich das erste Flugzeug im Punkt $A$ und das zweite Flugzeug im Punkt $C$ und beide flogen danach noch mindestens 4 Minuten mit konstanter Geschwindigkeit weiter. Der Parameter $t$ beschreibt also die Zeit in Minuten und beginnt bei $t= 0$ mit 8:00 Uhr.
Bestimme die Geschwindigkeit der beiden Flugzeuge in der Zeit zwischen 8:00 und 8:04 Uhr. Die Flugzeuge haben in den ersten 4 Minuten eine konstante Geschwindigkeit. Also kann man auch die Geschwindigkeit in der ersten Minute berechnen.
Das erste Flugzeug fliegt in einer Minute von $A(t= 0)$ nach $B(t= 1)$. Ebenso fliegt das zweite Flugzeug in einer Minute von $C(t= 0)$ nach $D(t= 1)$. Darum berechnen wir einerseits den Abstand von $A$ nach $B$ und andererseits den Abstand von $C$ nach $D$. Der Abstand kann mit dem Betrag des Richtungsvektors bestimmt werden.
\begin{align*}
|\overrightarrow{AB}|&=\sqrt{(\vec{b}-\vec{a})^2} = \sqrt{0^2+(-8)^2+0^2}=8 \notag \\
|\overrightarrow{CD}|&=\sqrt{(\vec{d}-\vec{c})^2} = \sqrt{6^2+6^2+1^2}=8,54 \notag
\end{align*}
Aufpassen: Der Richtungsvektor beschreibt die zurückgelegte Strecke in einer Zeiteinheit. Zudem muss an die Umrechnung der Einheiten gedacht werden. Geschwindigkeiten werden normalerweise in [km/h] angegeben. Wir haben die Geschwindigkeit in [km/min] ausgerechnet. Wie viele „Stunden“ sind eine Minute? Genau, wir ersetzen also [min] durch [$1/60$ h] und erhalten die Geschwindigkeiten:
\begin{align*}
v_1&=8 \ \textrm{[km/min]} \ = 480 \ \textrm{[km/h]} \notag \\
v_2&=8,54 \ \textrm{[km/min]} \ = 512 \ \textrm{[km/h]}. \notag
\end{align*}
