Gleichungen lösen
Um Gleichungen lösen zu können gibt es einige Standardtechniken, die wir euch auf dieser Seite zeigen. Wichtig ist, dass ihr diese Techniken verinnerlicht, denn sie werden euch nahezu täglich im Mathematikunterricht begegnen.
Inhaltsverzeichnis
- Gleichung lösen Grundlagen
- Bruchgleichungen lösen
- Ausklammern
- pq-Formel
- ABC-Formel
- Substitution
- Polynomdivision
- Newtonverfahren
- Gleichung mit e-Funktion lösen
- Ungleichungen lösen
1,99€
Gleichung lösen Grundlagen
Beispiel lineare Gleichung lösen
\begin{align*}
2x-8 & =0 \quad |+8 \\
2x & =8 \quad |:2 \\
x & =4
\end{align*}
Vorgehen
- Wir bringen die $8$ auf die rechte Seite, indem wir auf beiden Seiten der Gleichung 8 addieren.
- Wir dividieren beide Seiten durch 2, damit das $x$ auf der linken Seite der Gleichung alleine steht.
- Nach dem Dividieren sehen wir, dass die Gleichung x=4 „übrig“ geblieben ist. Somit ist 4 unser Ergebnis!
Beispiel Gleichung mit Wurzel lösen
\begin{align*}
2x^2- 8&= 0 \quad |+8 \\
2x^2 &= 8 \quad |:2 \\
x^2 &=4 \quad |\sqrt{ ~~} \\
x_1=2 \ &\wedge \ x_2=-2
\end{align*}
Vorgehen
- Wir bringen wieder die $8$ auf die rechte Seite, indem wir auf beiden Seiten der Gleichung 8 addieren.
- Wir dividieren beide Seiten durch 2, damit das $x$ auf der linken Seite der Gleichung alleine steht.
- Nach dem Dividieren sehen wir, dass die Gleichung $x^2=4$ „übrig“ geblieben ist. Wir müssen also die $x^2$ als nächstes abarbeiten.
- Wir ziehen auf beiden Seiten die Wurzel, damit das „hoch-zwei“ verschwindet. Wichtig: Wir erhalten zwei Ergebnisse, da wir die Wurzel gezogen haben! Diese sind $x_1=2 \ \ \textrm{und} \ \ x_2=-2$
Merksatz zu Gleichungen
Die Gleichung $x^2=a$ hat für
- $a>0$ die beiden Lösungen $x= \pm \sqrt{a}$,
- $a=0$ die einzige Lösung $x=0$,
- $a<0$ keine Lösung, denn es darf keine Wurzel aus einer negativen Zahl gezogen werden! Die Lösungsmenge ist in diesem Fall leer $\mathbb{L}=\{ \}$.
Beispiel Gleichung mit zwei „x“ lösen
\begin{align*}
2x+3=5x-12 \end{align*}
Beim Gleichungen lösen müssen wir uns überlegen, auf welcher Seite der Gleichung wir unsere $x$ und auf welcher Seite wir unsere Zahlen sammeln wollen. Es spielt grundsätzlich keine Rolle, ob das $x$ am Ende auf der linken oder auf der rechten Seite der Gleichung steht.
Wir entscheiden uns dafür, dass wir die $x$ auf der linken Seite sammeln und bringen jetzt die $5x$ mit $-5x$ auf die linke Seite der Gleichung:
\begin{align*}
\begin{array}{rrcll} &2x+3 & =& 5x-12 &|-5x \\ \Leftrightarrow & 2x+3-5x &=&5x-12-5x & \end{array} \end{align*}
Wir fassen zusammen und erhalten:
\begin{align*}
-3x+3=-12
\end{align*}
Als nächstes bringen wir die $3$ mit $-3$ auf die rechte Seite der Gleichung:
\begin{align*}
\begin{array}{rrcll} &-3x+3 & =& -12 &|-3 \\ \Leftrightarrow & -3x+3-3 &=&-12-3 & \end{array} \end{align*}
Wir fassen zusammen und erhalten:
\begin{align*}
-3x=-15
\end{align*}
Zum Schluss wollen wir noch die $-3$ vor unserem $x$ beseitigen. Wir teilen also auf beiden Seiten der Gleichung durch $-3$:
\begin{align*}
\begin{array}{rrcll} &-3x & =& -15 &|:(-3) \\ \Leftrightarrow & x &=&5 & \end{array} \end{align*}
Beispiel Gleichung mit Klammer lösen
Es kann auch vorkommen, dass unsere Gleichung zu Beginn Klammern enthält, die wir zuerst auflösen müssen:
\[2x-\left(3x+5\right)=2\cdot (x+3)\]
Ein Minus vor der Klammer bewirkt, dass sich die Vorzeichen in der Klammer umkehren und die Klammer anschließend verschwindet. Auf der rechten Seite unserer Gleichung wird die Klammer ausmultipliziert. Insgesamt erhalten wir also:
\[2x-3x-5=2x+6\]
Wir fassen zusammen und erhalten:
\[-x-5=2x+6\]
Merkt euch: $-x=-1\cdot x$
Wir bringen jetzt unsere $2x$ auf die linke Seite der Gleichung, indem wir $-2x$ rechnen und erhalten:
\begin{align*}
\begin{array}{rrcll} &-x-5 & =&2x+6 &|-2x \\ \Leftrightarrow & -3x-5 &=&6 & \end{array} \end{align*}
Anschließend bringen wir die $-5$ auf die rechte Seite der Gleichung, indem wir $+5$ rechnen:
\begin{align*}
\begin{array}{rrcll} &-3x-5 & =& 6 &|+5 \\ \Leftrightarrow & -3x &=&11 & \end{array} \end{align*}
Abschließend teilen wir auf beiden Seiten der Gleichung durch $-3$:
\begin{align*}
\begin{array}{rrcll} &-3x & =& 11 &|:(-3) \\ \Leftrightarrow & x &=&-\frac{11}{3} & \end{array} \end{align*}
Daniel erklärt euch nochmals im Video, wie ihr Gleichungen umformt und lösen könnt!
Bruchgleichungen lösen
Beim Bruchgleichungen Lösen geht ihr am besten nach dem folgenden Schema vor. (Hier geht es nochmal zu den Grundlagen des Bruchrechnens)
Zuerst werden die Nenner auf beiden Seiten der Gleichung eliminiert, indem ihr mit genau diesen beiden Nennern multipliziert. Anschließend verfahrt ihr genau so wie beim Lösen von linearen Gleichungen. Dazu gucken wir uns die folgende Gleichung an:
\begin{align*}
\begin{array}{rrcll} & \frac{2x+2}{3} & =& \frac{x-3}{2} &|\cdot 2 \\ \Leftrightarrow & \frac{(2x+2)\cdot 2}{3} & =& \frac{(x-3)\cdot 2}{2} & | \ \small{\textrm{Ausmultiplizieren bzw. Kürzen}} \\ \Leftrightarrow & \frac{4x+4}{3} & =& x-3 & |\cdot 3 \\ \Leftrightarrow & \frac{(4x+4)\cdot 3}{3} & =& (x-3)\cdot 3 & | \ \small{\textrm{Ausmultiplizieren bzw. Kürzen}} \\ \Leftrightarrow & 4x+4 & =& 3x-9 & |- 3x \\ \Leftrightarrow & x+4 & =&-9 & |- 4 \\ \Leftrightarrow & x & =&-13 & \end{array} \end{align*}
Der folgende Trick kann beim Lösen von Bruchgleichungen besonders hilfreich sein. Sollte euer $x$ im Nenner stehen, so dürft ihr auf beiden Seiten der Gleichung den Kehrwert bilden und könnt anschließend wieder mit dem jeweiligen Nenner multiplizieren:
\begin{align*}
\begin{array}{rrcll} &\frac{2}{x} & =& \frac{32}{7} &|\ \small{\textrm{Kehrwert bilden}} \\ \Leftrightarrow &\frac{x}{2} & =& \frac{7}{32} & | \cdot 2 \\ \Leftrightarrow &\frac{x \cdot 2}{2} & =& \frac{7 \cdot 2 }{32} & | \ \small{\textrm{Ausmultiplizieren bzw. Kürzen}} \\ \Leftrightarrow & x & =& \frac{14}{32} = \frac{7}{16} & \\ \end{array} \end{align*}
Ausklammern
\begin{align*}
;x^3- \frac{1}{4}x^5&= 0 \quad |\ \textrm{grösste gemeinsame x ausklammern!} \\
;\Leftrightarrow \quad \underbrace{\underbrace{x^3}_{\textrm{Faktor}} \cdot \underbrace{\left(1-\frac{1}{4}x^2\right)}_{\textrm{Faktor}}}_{\textrm{Produkt}}&= 0
\end{align*}
Nach dem Ausklammern bestimmt ihr für den Teil in der Klammer und den Teil außerhalb der Klammer jeweils separat die Nullstellen.
\begin{align*}
x^3&=0 \quad \textrm{oder} \quad 1-\frac{1}{4}x^2=0 \\
x_1&=0 \Leftrightarrow x_2=2 \wedge\ x_3=-2
\end{align*}
Hinweis: Dieser Lösungsweg ist nur dann sinnvoll, wenn keine Zahl ohne $x$ vorkommt!
Schau dir per Video an, wie Nullstellen mit dem Lösungsverfahren gelöst werden!
pq-Formel
Um die pq-Formel verwenden zu können, müssen quadratische Gleichungen (höchste Potenz ist 2) in die Form
\begin{align*}
x² + px + q = 0
\end{align*}
gebracht werden, so dass beim $x²$ kein Vorfaktor mehr steht. Anschließend
kann die pq-Formel verwendet werden und man erhält die Lösungen
\begin{align*}
x_{1,2} = -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2} \right)^2 – q}. tag
\end{align*}
Beispiel Gleichung mit PQ-Formel lösen
\begin{align*}
2x^2-4x-16&= 0 \quad |:2 \\
x^2 -2x-8 &= 0 \quad |\ \textrm{pq-Formel} \\
&\Rightarrow \quad x_{1,2} = -\frac{-2}{2} \pm \sqrt{\left(\frac{-2}{2} \right)^2 – (-8)} \\
& \Leftrightarrow \quad x_1=4 \ \wedge \ x_2=-2
\end{align*}
1,99€
1. Beispiel Gleichung mit PQ-Formel lösen
(Keine Lösung $\Rightarrow$ Der Graph der Funktion schneidet die x-Achse nicht, es gibt keine Nullstelle)
\begin{align*}
f(x) &=x^2-2x+3 \quad \textrm{mit } p = -2 \ \textrm{und } q=3 \\ \\
\Rightarrow x_{1,2} &= -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2} \right)^2 – q} \quad = \quad -\frac{-2}{2} \pm \sqrt{\left(\frac{-2}{2} \right)^2 – 3} \\ \\
\Leftrightarrow x_{1,2} &= 1 \pm \sqrt{( -1 )^2 – 3} \quad = \quad 1 \pm \sqrt{1 – 3} = 1 \pm \sqrt{-2}
\end{align*}
Unsere Berechnung müssen wir an dieser Stelle abbrechen, da es nicht möglich ist, die Wurzel aus einer negativen Zahl zu ziehen.
2. Beispiel Gleichung mit PQ-Formel lösen
(Eine Lösung $\Rightarrow$ Der Graph der Funktion berührt die Funktion an genau einer Stelle, es gibt also eine Nullstelle)
\begin{align*}
f(x) &=x^2-2x+1 \quad \textrm{mit } p = -2 \ \textrm{und } q=1 \\ \\
\Rightarrow x_{1,2} &= -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2} \right)^2 – q}\quad =\quad -\frac{-2}{2} \pm \sqrt{\left(\frac{-2}{2} \right)^2 – 1} \\ \\
\Leftrightarrow x_{1,2} &= 1 \pm \sqrt{( -1 )^2 – 1} \quad = \quad 1 \pm \sqrt{1 – 1} = 1 \pm \sqrt{0} \\ \\
x_{1} &= 1 + 0 \quad \wedge \quad x_{2}= 1 – 0 = 1
\end{align*}
Beide Berechnungen liefern dasselbe Ergebnis! Es gibt also nur eine Lösung.
3. Beispiel Gleichung mit PQ-Formel lösen
(Zwei Lösungen $\Rightarrow$ Der Graph der Funktion schneidet die x-Achse an genau zwei Stellen, es gibt also zwei Nullstellen)
\begin{align*}
f(x) &=x^2-2x-3 \quad \textrm{mit } p = -2 \ \textrm{und } q=-3 \\ \\
\Rightarrow x_{1,2} &= -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2} \right)^2 – q} = -\frac{-2}{2} \pm \sqrt{\left(\frac{-2}{2} \right)^2 – (-3)} \\ \\
\Leftrightarrow x_{1,2} &= 1 \pm \sqrt{( -1 )^2 – (-3)} = 1 \pm \sqrt{1 + 3} = 1 \pm \sqrt{4} \\ \\
\Leftrightarrow 1 \pm 2
x_{1} &= 1 + 2 = 3 \quad \wedge \quad x_{2}= 1 – 2 = – 1
\end{align*}
Im Allgemeinen lässt sich aus diesen drei Beispielen eine einfache Regel herleiten. Ausschlaggebend für die Anzahl unserer Nullstellen ist immer der Wert des Terms, welcher unter der Wurzel steht, die sogenannte Diskriminante.
Nimmt die Diskriminante einen negativen Wert an, so haben wir keine Nullstelle, nimmt sie den Wert 0 an, so haben wir eine Nullstelle und nimmt sie einen positiven Wert an, so haben wir zwei Nullstellen.
\begin{align*}
&D < 0 \Rightarrow keine Nullstelle \\
&D = 0 \Rightarrow eine Nullstelle \\
&D > 0 \Rightarrow zwei Nullstellen \\
\end{align*}
Daniel erklärt euch nochmal alles rund um das Thema pq-Formel!
ABC-Formel
Auch Mitternachts-Formel genannt, kann alternativ zur pq-Formel verwendet werden. Die quadratische Gleichung
\begin{align*}
ax² + bx + c = 0
\end{align*}
lässt sich direkt lösen. Das Ergebnis lautet
\begin{align*}
x_{1,2} = \frac{-b \pm \sqrt{ b^2 – 4ac}}{2a}.
\end{align*}
Beispiel zur ABC-Formel
\begin{align*}
2x^2-4x-16&= 0 \\
\Rightarrow \quad x_{1,2} &= \frac{-(-4) \pm \sqrt{ (-4)^2 – 4 \cdot 2 \cdot (-16)}}{2 \cdot 2} \\
&= \frac{4 \pm \sqrt{16+128}}{4} \\
x_1=4 \ &\wedge \ x_2=-2
\end{align*}
Hier bekommst du nochmals die Mitternachtsformel per Video erklärt!
Substitution
Gucken wir uns folgende Gleichung an:
\begin{align*}
x^4-2x^2-8&=0
\end{align*}
Uns fällt sofort auf, dass nur gerade Exponenten auftreten. Um diese Gleichung Lösen zu können, ersetzen wir $x^2$ durch $z$ und erhalten wieder eine quadratische Gleichung, die mit der
PQ-Formel gelöst werden kann. Nach dem Lösen darf aber nicht die Rücksubstitution vergessen werden!
\begin{align*}
x^4-2x^2-8=0 \quad \stackrel{x^2=z}{\Longrightarrow} \quad z^2-2z-8=0
\end{align*}
Mit der PQ-Formel erhalten wir dann die Lösungen:
\begin{align*}
z_1=4 \ \wedge\ \ z_2=-2
\end{align*}
Bei der Rücksubstitution müssen wir, wie der Name schon sagt, wieder zurück ersetzen. Es folgt:
\begin{align*}
z_1&=4 \quad \ \stackrel{z_1=x_1^2}{\Longrightarrow} \quad x_1^2= 4 \quad \Leftrightarrow \quad x_1=2 \wedge x_2=-2 \\
z_2&=-2 \ \ \stackrel{z_2=x_3^2}{\Longrightarrow} \quad x_3^2= -2: \ \textrm{Wurzel aus negativer Zahl nicht moeglich}
\end{align*}
Hier kannst du dir das gesamte Thema nochmals in Ruhe anschauen!
Polynomdivision
Falls eine Gleichung vorliegt, die nicht mit den obigen Verfahren gelöst werden kann, muss oft die Polynomdivision verwendet werden – oder der Taschenrechner. Beispiel:
\begin{align*}
f(x)=2x^3-7x^2+10x-5
\end{align*}
Der Trick ist es, eine Nullstelle zu erraten oder sie dem Aufgabentext zu entnehmen. Wir wissen, dass die Nullstelle ein Vielfaches oder ein Teiler des Absolutgliedes ist, also von der Zahl der Gleichung, die kein $x$ enthält. Somit erraten wir die Nullstelle $x_1=1$.
\begin{align*}
\textrm{Probe:} \quad f(1)=2 \cdot 1^3-7 \cdot 1^2+10 \cdot 1-5=0.
\end{align*}
Kommen wir nun zur Polynomdivision, das Vorgehen kennt ihr schon aus der Divisionsrechnung aus der Grundschule! Ihr nehmt eure Ausgangsfunktion teilt diese durch ($x-$Nullstelle), also in diesem Fall $x-1$
\begin{align*}
(2x^3-7x^2+10x-5):(x-1)= ??
\end{align*}
Schauen wir uns nun die rechte Klammer $(x-1)$ an. Es muss eine Zahl mit dem $x$ der Klammer multipliziert werden, damit der erste Term der ersten Klammer, hier $2x^3$, herauskommt. In diesem Fall wäre das $2x^2$. Nun wird $2x^2$ mit $(x-1)$ multipliziert und von der ersten Klammer subtrahiert. Das Ergebnis wird drunter geschrieben und der Vorgang wird solange wiederholt, bis wir zu einem Resultat kommen.
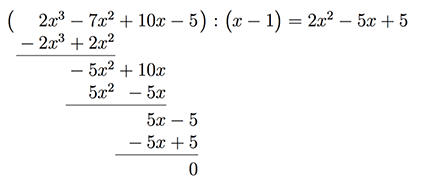
Das Ergebnis $2x^2-5x+5$ der Polyonmdivision kann mit der pq-Formel gelöst werden.
Beim Aufschreiben der Lösungsmenge darf die geratene Nullstelle nicht vergessen werden.
Newtonverfahren
Das Newtonverfahren ist ein Näherungsverfahren zur Bestimmung der Nullstellen.
Bei einfachen Termen ist man sicherlich mit den anderen Methoden schneller, werden die Funktionen komplexer und reichen eure mathematischen Regeln nicht mehr aus, greift man zum Newtonverfahren. Dazu verwendet man folgende Formel.
\begin{align*}
x_{\textrm{neu}}=x_{\textrm{start}}-\frac{f(x_n)}{f'(x_n)}
\end{align*}
Im Genaueren bedeutet es, dass wir einen Startwert $x_{\textrm{start}}$ selbst bestimmen müssen, diesen in die Formel einsetzen um $x_{\textrm{neu}}$ zu erhalten.
Wenn man dieses Verfahren öfter wiederholt, werdet ihr merken, dass sich irgendwann der Wert des Ergebnisses nicht mehr bzw. kaum ändert. Erst dann können wir den Wert verwenden.
Das Newtonverfahren wollen wir an dem folgenden Beispiel kurz durchspielen. Als willkürlichen Startwert wählen wir $x_\textrm{start}=18$.
\begin{align*}
x^3-15x^2-175=0
\end{align*}
\begin{array}{c|c|c|c}
x_{\textrm{start}} & f(x) & f'(x) & x_{\textrm{neu}} = x_{\textrm{start}}-\frac{f(x)}{f'(x)} \\
\hline
18 & 797 & 432 & 16,16 \\
16,16 & 127,93 & 298,64 & 15,73 \\
15,73 & 5,63 & 270,40 & 15,71 \\
\end{array}
Wie wir sehen ändert sich der $x$-Wert bereits beim 2. Schritt nicht mehr stark (von $15,73$ auf $15,71$)! Beim nächsten Schritt kann es schon passieren, dass sich nur noch die Nachkommastellen ändern.
Wir könnten sagen, dass die Nullstelle ungefähr bei $15,71$ liegt.
1,99€
Lass dir von Daniel nochmal die Polynomdivision per Video erklären!
Gleichung mit e-Funktion lösen
Zur Lösung von Gleichungen mit $e$-Funktionen verwendet man in der Regel ihre Umkehrfunktion, den natürlichen Logarithmus ln.
Ein nützlicher Zusammenhang ist
\begin{align*}
e^{\ln(x)} = x \quad \textrm{bzw.} \quad \ln(e^x)=x.
\end{align*}
Achtet auf die Logarithmengesetze! Es folgen einige Beispiele zum Lösen von Gleichungen mit $e$-Funktionen:
\begin{align*}
e^{2x}\cdot (x^2-2) = 0 \\
e^{2x}= 0 \ \vee \ x^2-2&=0 \quad |+2 \\
x^2&=2 \quad |\sqrt{ ~~} \\
x_1=\sqrt{2} \ &\wedge \ x_2=-\sqrt{2}
\end{align*}
Warum bringt $e^{2x}= 0$ keine Lösung?
Wenn man beide Seite logarithmiert folgt $\ln(2x)=\ln(0)$.
Da der natürliche Logarithmus aber für 0 nicht definiert ist ($\mathbb{D}=(0,\infty))$, gibt es keine Lösung.
\begin{align*}
\begin{array}{lrcll}
a) & 8e^{-2x}-16 & = & 0 & \quad |+16 \\
\Leftrightarrow \quad & 8e^{-2x} & = & 16 & \quad |:8 \\
\Leftrightarrow \quad & e^{-2x} &= & 2 & \quad | \ln \\
\Leftrightarrow \quad & \ln(e^{-2x}) & = & \ln(2) & \\
\Leftrightarrow \quad & -2 x & = & \ln(2) & \quad |:(-2) \\
\Leftrightarrow \quad & x & =& -\ln(2)/2 &
\end{array}
\end{align*}
\begin{align*}
\begin{array}{lrcll}
b) & 4e^{3x}-e^{2x} & = & 0 & \quad |+e^{2x} \\
\Leftrightarrow \quad & 4e^{3x} & = & e^{2x} & \quad | \ln \\
\Leftrightarrow \quad & \ln(4 \cdot e^{3x}) &=& \ln(e^{2x}) & \\
\Leftrightarrow \quad & \ln(4)+\ln(e^{3x}) & =& 2x & \\
\Leftrightarrow \quad & \ln(4)+3x & =& 2x &\quad |-3x \\
\Leftrightarrow \quad & \ln(4) & =& -1x &\quad |\cdot (-1) \\
\Leftrightarrow \quad & -\ln(4) & =& x &
\end{array}
\end{align*}
Wie du Nullstellen mit dem Newtonverfahren bestimmen kannst, zeigt dir Daniel nochmal per Video!
Ungleichungen lösen
Das Thema Ungleichungen wird häufig nicht in der Schule behandelt. Wir wollen uns dieses Thema jedoch kurz angucken und die wichtigsten Regeln festhalten. Grundsätzlich dürfen Ungleichungen nach denselben Regeln wie Gleichungen gelöst werden.
Es gibt eine Ausnahme. Sobald ihr die Ungleichung mit einer negativen Zahl multipliziert oder durch eine negative Zahl teilt, muss das Ungleichzeichen seine Richtung ändern. Beispiel:
\begin{align*}
\begin{array}{rrcll} &-3x + 7 & < & -6x-5 &|+3x \\ \Leftrightarrow & 7 &<& -3x-5 & |+5 \end{array} \end{align*}
Bis jetzt sind wir genau so verfahren, als würde es sich um eine lineare Gleichung handeln. Aber jetzt kommt die vorhin erwähnte Ausnahme. Wir teilen unsere Ungleichung durch $-3$ und müssen nun also unser Ungleichzeichen umdrehen:
\begin{align*}
\begin{array}{rrcll} &12 & < & -3x &|:(-3) \\ \Leftrightarrow & -4 &>& x & \end{array} \end{align*}
Beachte: $\mathrm{\ -4>x}$ ist das gleiche wie $\mathrm{\ x<-4}$.
Schaut euch auch auf jeden Fall die Playlist zum Thema Gleichungen lösen an.