
Kombinatorik
Erinnern wir uns an dieser Stelle an den Quotienten der Laplace -Wahrscheinlichkeit:
\begin{align*}
P(A) = \frac{\textrm{Anzahl der guenstigen Ergebnisse}}{\textrm{Anzahl der moeglichen Ergebnisse}}
\end{align*}
Bei der Bestimmung dieses Quotienten bedient man sich der Kombinatorik. Dort veranschaulicht man Ergebnisse für Zufallsexperimente mit endlicher Ergebnismenge häufig anhand des Urnenmodells – gedanklich ein Gefäß mit $n$ durchnummerierten Kugeln, von denen $k$ zufällig ausgewählt werden.
Neu!
Die Auswahl der Kugeln ist als Ziehung einer Zufallsstichprobe des Umfangs $k$ aus einer Grundgesamtheit mit $n$ Elementen zu interpretieren. Wenn jede denkbare Stichprobe des Umfangs $k$ mit gleicher Wahrscheinlichkeit realisiert wird, liegt eine einfache Zufallsstichprobe vor.
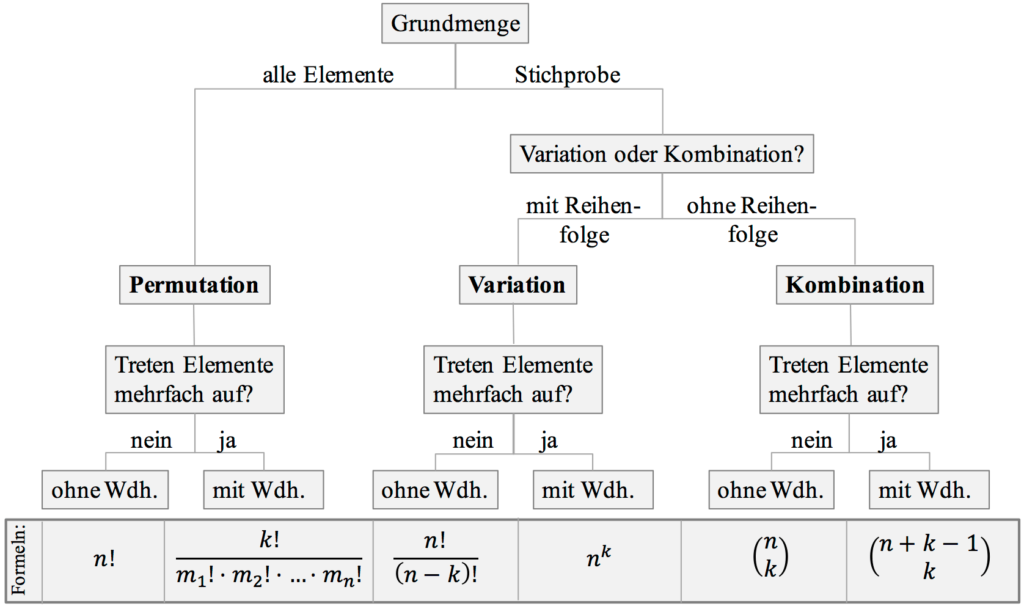
Wie viele Möglichkeiten der Auswahl der $n$ Elemente es gibt, hängt davon ab, ob die Elemente der Stichprobe nach der Ziehung jeweils wieder zurückgelegt werden oder nicht (Urnenmodell bzw. Stichprobenziehung mit/ohne Zurücklegen).
Die Anzahl der Möglichkeiten hängt auch davon ab, in welcher Reihenfolge die $n$ nummerierten Kugeln gezogen werden (Stichprobenziehung mit/ohne Berücksichtigung der Anordnung).
Formeln für die Berechnung der Anzahl der Möglichkeiten der Ziehung einer Stichprobe des Umfangs $k$ aus einer Grundgesamtheit mit $n$ Elementen in allen 6 Fällen sind obiger Übersicht zusammenfassend dargestellt.
Der Binomialkoeffizient ist definiert durch:
\begin{align*}
\begin{pmatrix} n \\ k \end{pmatrix} = \frac{n!}{(n-k)!\cdot k!}
\end{align*}
Besondere Fälle:
$\begin{pmatrix} n \\ 0 \end{pmatrix} = 1$ und $\begin{pmatrix} k \\ 1 \end{pmatrix} = k$ sowie $\begin{pmatrix} n \\ n \end{pmatrix} = 1$.
Die Fakultät $k!=1 \cdot 2 \cdot 3 \cdot … \cdot k$ ist das Produkt aus allen natürlichen Zahlen von 1 bis $k$. Weiterhin solltet ihr wissen, dass $0!=1$ ist.
Welche Formel brauche ich?
- Entscheide, ob alle Elemente betrachtet werden oder nur eine Stichprobe.
- Entscheide, ob die Reihenfolge/Anordnung wichtig ist.
- Entscheide, ob eine Wiederholung der Elemente möglich ist .
- Formel auswählen.
- Wähle $n$ und $k$.
Merke: $k$ ist immer etwas, von dem wir die Möglichkeiten/Wahrscheinlichkeit wissen möchten und $n$ sind immer die Elemente, die wir zur Verfügung haben.
Neu!
Beispiele
Peter hat ein Zahlenschloss mit vier Ziffern. Er hat bei den ganzen Abiparties seinen Code vergessen. Er fragt sich nun, wie viele Möglichkeiten er hat, um sein Schloss wieder zu öffnen. Hierfür arbeiten wir das obige Vorgehen ab:
1) Entscheide ob alle Elemente betrachtet werden oder nur eine Stichprobe.Stichprobe, da Ziffern von $[0-9]$ zur Verfügung stehen, aber nur vier Ziffern genutzt werden.
2) Entscheide ob die Reihenfolge/Anordnung wichtig ist.Die Reihenfolge beim Zahlenschloss ist wichtig, da $[1,2,3,4]$ eine andere Variation des Codes ist als $[1,3,2,4]$.
3) Entscheide ob eine Wiederholung der Elemente möglich ist.Eine Wiederholung der Elemente bei einem Zahlenschloss ist möglich $[2,2,1,4]$.
4) Formel auswählen: $n^k$
5) Wähle $n$ und $k$:In diesem Beispiel sind die Ziffern $[0-9]$ die Elemente, die wir zur Verfügung haben und entnehmen aus dieser Grundgesamtheit vier Elemente, die uns interessieren.
\begin{align*}
10^4=10000 ~\textrm{Möglichkeiten}
\end{align*}
Beim Osterlauf in Paderborn nehmen 10 Rennläufer teil. Wie viele Möglichkeiten gibt es für Gold, Silber und Bronze?Hierfür arbeiten wir auch wieder das obige Vorgehen ab:
1) Entscheide ob alle Elemente betrachtet werden oder nur eine Stichprobe.Stichprobe, da nur die ersten drei Plätze von Interesse sind, es aber zehn Rennläufer gibt.
2) Entscheide ob die Reihenfolge/Anordnung wichtig ist.Die Reihenfolge/Anordnung ist wichtig, da Gold, Silber und Bronze von Interesse ist.
3) Entscheide ob eine Wiederholung der Elemente möglich ist.Eine Wiederholung ist nicht möglich, da der Rennläufer der Gold gewonnen hat nicht gleichzeitig auch Silber gewinnen kann.
4) Formel auswählen: $\frac{n!}{(n-k)!}$
5) Wähle $n$ und $k$:In diesem Beispiel sind die zehn Rennläufer die Grundgesamtheit ($n=10$), die zur Verfügung steht. Von Interesse sind hier die ersten drei Plätze ($k=3$).
\begin{align*}
\frac{10!}{(10-3)!} = \frac{10!}{7!} = 10 \cdot 9 \cdot 8 = 720 ~\textrm{Möglichkeiten}
\end{align*}
Neu!
Wie viele Möglichkeiten gibt es, fünf verschiedene Stochastik-Bücher in ein Regal nebeneinander zu stellen? Hierfür arbeiten wir auch wieder das obige Vorgehen ab:
1) Entscheide ob alle Elemente betrachtet werden oder nur eine Stichprobe.In diesem Beispiel werden alle Elemente in der Aufgabenstellung betrachtet und nicht etwa eine Stichprobe von drei Büchern erfragt.
2) Entscheide ob die Reihenfolge/Anordnung wichtig ist.Wenn man Elemente betrachtet, dann verwendet man die Permutation, die immer geordnet ist.
3) Entscheide ob eine Wiederholung der Elemente möglich ist.Es ist keine Wiederholung möglich, da die Stochastik-Bücher verschiedenartig sind, somit jedes Element nur einmal existiert. (Signalwort: „verschiedene“).
4) Formel auswählen: $n!$
5)Wähle $n$:Zu wählen sind alle Elemente in der Aufgabenstellung.
\begin{align*}
5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120 ~\textrm{Möglichkeiten}
\end{align*}
Schau dir zur Vertiefung und Wiederholung Daniels Playlist zu Kombinatorik an.

