Komplexe Zahlen

Komplexe Zahlen (Symbol: $z$ ) stellen eine Erweiterung des Zahlenbereichs dar. Diese Erweiterung ist notwendig um Gleichungen wie z.B. $x^2=-1$ lösen zu können. Für diese Gleichung finden wir keine reelle Zahl aus $\mathbb{R}$, die diese Gleichung lösen würde.

Komplexe Zahlen können in der Form $z = a+b\cdot i$ dargestellt werden. Der Teil $a + b$ der Funktion wird Realteil- und $i$ Imaginärteil genannt.

Themen auf dieser Seite

• Grundlagen komplexer Zahlen
• Darstellungsformen komplexer Zahlen
• Komplexe Folgen und Reihen
• Übersicht von Rechenregeln

Grundlagen komplexer Zahlen

Schau dir zu Beginn das Lernvideo zu komplexe Zahlen an

Komplexe Zahlen sind aufgrund ihrer Konstruktion auf der komplexen Zahlenebene angeordnet.

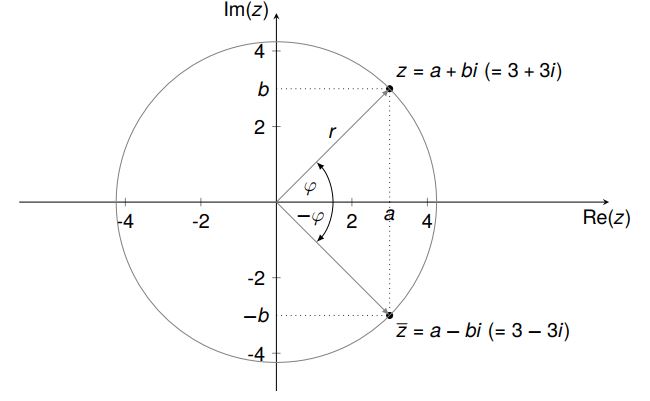
Eine komplexe Zahl ist aus folgenden Teilen zusammengesetzt:
$ \quad z=a+bi$

Realteil Re(z) und Imaginärteil Im(z):
$\quad$Re(z) = $a \in \mathbb{R}$
$\quad$Im(z) = $b \in \mathbb{R} \quad$ Beachte: Im(z) $\neq bi$!

Betrag |z| und Argument $\varphi$:
$\quad |z|=r=\sqrt{(\textrm{Re{z}})^2+(\textrm{Im{z}})^2}=\sqrt{a^2+b^2}\\
\quad \varphi=\arg(z)\quad \textrm{Winkel zw. pos. Re-Achse und Strecke}\ \ \overline{0z}$

Zu jeder komplexen Zahl $z$ gibt es dessen komplex Konjugierte $\overline{z}$:
$\quad \overline{z} = a – bi$

Imaginäre Einheit $i$:
$\quad i^2 = -1$

Entgegen vieler Schreibweisen und Internetquellen ist $i$ rein mathematisch $\textit{nicht}$ gleichzusetzen mit $\sqrt{-1}$.

Folgende Rechnung zeigt den Konflikt in der Annahme es gäbe $\sqrt{-1}$ und es könne damit gerechnet werden. vgl. $\ast^2$: Das „$=$“ wäre ohne die Annahme der Existenz von $\sqrt{-1}$ nämlich ebenfalls nicht korrekt!. Ab $\ast^1$ geht dann die Rechnung schief und es entsteht ein Widerspruch:

\begin{align*}
\quad -1=i^2=i\cdot i =^{\ast^1} \ \sqrt{-1}\cdot\sqrt{-1} =^{\ast^2} \ \sqrt{(-1)(-1)}=\sqrt{1}=1\quad \Longrightarrow -1 \neq 1
\end{align*}

Darstellungsformen komplexer Zahlen

Da sich die komplexen Zahlen auf einer Ebene befinden, nutzen wir für eine eindeutige Zuordnung der Zahlen Polarkoordinaten. Damit lassen sich die Zahlen in die $\textit{Polarform}$ überführen. Diese Darstellung hat bei vielen Berechnungen Vorteile gegenüber der klassischen $\textit{kartesischen Darstellung}$ der Zahlen.

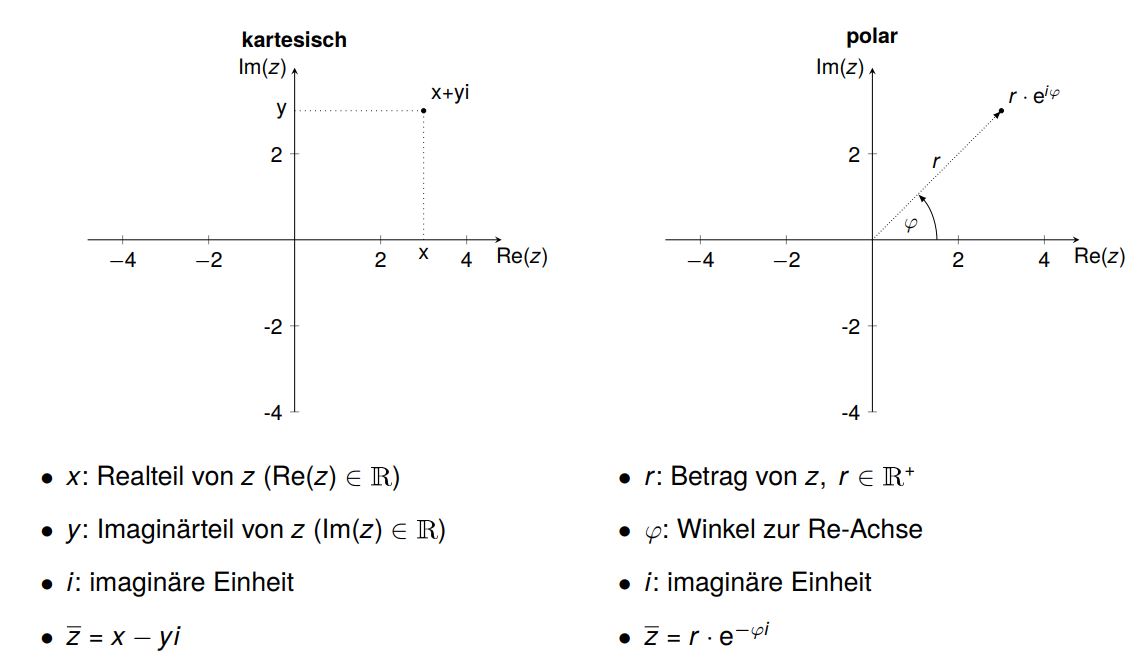
Wie wir der Grafik entnehmen können, wird eine komplexe Zahl entweder durch seinen Real- und Imaginärteil oder durch „Betrag und Argument“ definiert:

$\quad \text{Kartesisch }z=a+bi $
$\quad \text{Polar }z=r\exp^{\varphi i} $

Dass die Polarform durch die e-Funktion beschrieben wird, ergibt Sinn, da die e-Funktion im Komplexen abhängig von Betrag und Argument ist. Reduzieren wir diese auf reelle Zahlen, so ergibt sich wieder die übliche Exponentialfunktion, wie schon aus der Schule bekannt.

Darstellungen umwandeln

Kartesische in die Polarform

$r=\sqrt{\textrm{Re{z}}^2+\textrm{Im{z}}^2}$
$\varphi=\begin{cases}\arccos\left(\frac{\textrm{Re{z}}}{r}\right)&\text{für }\textrm{Im{z}} \geq 0\\ 2\pi-\arccos\left(\frac{\textrm{Re{z}}}{r}\right)&\text{für }\textrm{Im{z}} < 0\end{cases}$

Polarform in die Kartesische

$\quad \textrm{Re{z}}=r\cdot \cos(\varphi)$
$\quad \textrm{Im{z}}=r\cdot \sin(\varphi)$

Beispiele zur Umwandlung komplexer Zahlen

Von Kartesisch nach Polar:
\begin{align*}
z&=3+\sqrt{3}\cdot i\qquad\text{mit}\\
&\qquad r=\sqrt{9+3}=\sqrt{12}\\
&\qquad \varphi\stackrel{\sqrt{3}>0}{=}\arccos\left(\frac{3}{\sqrt{12}}\right)=\arccos\left(\frac{\sqrt{3^2}}{\sqrt{3\cdot 4}}\right)=\arccos\left(\frac{\sqrt{3}}{2}\right)=\frac{\pi}{6}\\
z&=2\sqrt{3}\cdot\exp^{\frac{\pi}{6}\cdot i}
\end{align*}

Von Polar nach Kartesisch:
\begin{align*}
z&=2\cdot \exp^{\frac{5}{4}\pi i}\qquad\text{mit}\\
&\qquad \textrm{Re{z}}=2\cos\left(\frac{5}{4}\pi\right)=2\cos\left(\pi+\frac{1}{4}\pi\right)=2\Bigl(-\cos\left(\frac{1}{4}\pi\right)\Bigr)=-2\frac{1}{\sqrt{2}}\\
&\qquad \textrm{Im{z}}=2\sin\left(\frac{5}{4}\pi\right)=2\sin\left(\pi+\frac{1}{4}\pi\right)=2\Bigl(-\sin\left(\frac{1}{4}\pi\right)\Bigr)=-2\frac{1}{\sqrt{2}}\\
z&=\sqrt{2}+\sqrt{2}\cdot i
\end{align*}

Übersicht von Rechenregeln

Es gelten alle Rechengesetze für Zahlen aus $\mathbb{C}$, wie wir sie für die Zahlen aus $\mathbb{R}$ kennen. Es muss lediglich aufgepasst werden, dass sich Real- und Imaginärteile in Rechnungen nicht vermischen. Das $i$ kannst du somit wie eine Variable ansehen.

Für kartesische Darstellung gilt…
$\quad z_1 = a + bi \textrm{ und } z_2 = c + di \textrm{ sowie } n \in \mathbb{N}$

Addition von komplexen Zahlen
$\quad z_1+z_2=(a+c)+(b+d)i$

Multiplikation von komplexen Zahlen
$\quad z_1\cdot z_2=(ac-bd)+(ad+bc)i$

Division von komplexen Zahlen
$\quad \frac{z_1}{z_2}=\frac{z_1\overline{z_2}}{z_2\overline{z_2}}=\frac{(a+bi)(c-di)}{c^2+d^2}=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i$

Potenzieren komplexer Zahlen
$\quad z_1^n=\ldots\text{nicht empfehlenswert ab }n\geq 5$
$\quad z_1^{z_2}=\ldots\text{nicht empfehlenswert}$

Wurzel einer komplexen Zahl ziehen
$\quad \sqrt[n]{z_1}=\ldots\text{nicht empfehlenswert}$

Für Polarform gilt…

$\quad z_1=r_1\cdot\exp^{\varphi_1i} \textrm{ und } z_2=r_2\cdot\exp^{\varphi_2i} \textrm{ sowie } n\in\mathbb{N}$
Addition
$\quad z_1+z_2=\ldots\text{nicht empfehlenswert} $

Produkt
$\quad z_1\cdot z_2=(r_1\cdot r_2)\cdot\exp^{(\varphi_1+\varphi_2)i} $

Division
$\quad \frac{z_1}{z_2}=\frac{r_1\cdot\exp^{\varphi_1i}}{r_2\cdot\exp^{\varphi_2i}}=\frac{r_1}{r_2}\cdot\exp^{(\varphi_1-\varphi_2)i}$

Potenzieren
$\quad z_1^n=\left(r_1\cdot\exp^{\varphi_1i}\right)^n=r_1^n\cdot\exp^{n\varphi_1i}$
$\quad z_1^{z_2}=\exp^{z_2\cdot\ln(z_1)}\quad\text{mit}\quad z_2\cdot\ln(z_1) = r_2\exp^{\varphi_2i}\cdot\bigl(\ln(r_1)+\varphi_1i\bigr)$
$\quad \quad \text{dann } z_2 \textrm{ in kartesische Darstellung umwandeln}$

Wurzel ziehen
$\quad \sqrt[n]{z_1}=\ldots\text{verwende Produkt-Gleichung}$

Allgemein lässt sich bei gewissen Rechenoperationen eine Parallele zur Vektorrechnnug im $\mathbb{R}^2$ erkennen:

Werden komplexe Zahlen Multipliziert (dividiert), werden die Beträge multipliziert (dividiert) und die Argumente addiert (subtrahiert).

Auswahl komplexer Funktionen und komplexer Wurzeln

Ausgewählte Funktionen:

Komplexe e-Funktion
$\quad \exp^{z}=\exp^{\Re{z}}\Bigl(\cos\bigl(\textrm{Im{z}}\bigr)+i\sin\bigl(\textrm{Im{z}}\bigr)\Bigr)\qquad\text{damit gilt auch}$
$\quad r\cdot\exp^{\varphi i}=r\cdot\Bigl(\cos\bigl(\varphi\bigr)+i\sin\bigl(\varphi\bigr)\Bigr)$

Komplexer Logarithmus (Für z in Polarform gilt)
$\quad \ln{(z)}=\ln{(r\exp^{\varphi i})}=\ln(r)+\varphi i$

Komplexe trigonometrische Funktionen
$\quad \sin(z)=\frac{1}{2i}\left(\exp^{iz}-\exp^{-iz}\right)$
$\quad \cos(z)=\frac{1}{2}\left(\exp^{iz}+\exp^{-iz}\right)$

Komplexes Wurzelziehen (Für z in Polarform gilt)
$\quad \sqrt[n]{z}=\sqrt[n]{r}\cdot \text{exp}\left\{\frac{\varphi+2k\pi}{n}\cdot i\right\},\quad \forall\,k\in\{0,1,\ldots,n-1\}$

Beispiel zu „Komplexes Wurzelziehen“ für z in Polarform

Die Formel zu Komplexes Wurzelziehen wirkt kompliziert. Darum stellen wir euch eine Beispielrechnung samt Skizze zur Verfügung:

Finde alle Lösungen der Gleichung $z^5=3-3\sqrt{3}$.

Zunächst wandeln wir wieder von kartesisch nach polar um:

\begin{alignat*}{2}
&3-3\sqrt{3}\cdot i\qquad\text{mit}\\
&\qquad r=\sqrt{9+9\cdot 3}=\sqrt{36}=6\\
&\qquad \varphi\stackrel{-3\sqrt{3}<0}{=}2\pi-\arccos\left(\frac{3}{6}\right)=2\pi-\frac{\pi}{3}=\frac{5}{3}\pi\\
\rightarrow\ &3-3\sqrt{3}\cdot i\ =6\cdot\exp^{\frac{5}{3}\pi\cdot i}
\end{alignat*}
Damit gilt für z:
\begin{align*}
\Rightarrow\ z&=\sqrt[5]{z_1}=\sqrt[5]{6}\cdot\text{exp}\left\{\frac{\frac{5}{3}\pi+2k\pi}{5}\cdot i\right\}=\sqrt[5]{6}\cdot\text{exp}\left\{\biggl(\frac{1}{3}\pi+\frac{2}{5}k\pi\biggr)\cdot i\right\}\\
&=\sqrt[5]{6}\cdot\text{exp}\left\{\biggl(\frac{5}{15}\pi+\frac{6}{15}k\pi\biggr)\cdot i\right\},\quad \forall\,k\in\{0,1,2,3,4\}
\end{align*}
Also sind die Lösungen:

\begin{alignat*}{3}
&z_1&&=\sqrt[5]{6}\cdot\exp^{\frac{1}{3}\cdot \pi\cdot i}&&\qquad(k=0)\\
&z_2&&=\sqrt[5]{6}\cdot\exp^{\frac{11}{15}\cdot \pi\cdot i}&&\qquad(k=1)\\
&z_3&&=\sqrt[5]{6}\cdot\exp^{\frac{17}{15}\cdot \pi\cdot i}&&\qquad(k=2)\\
&z_4&&=\sqrt[5]{6}\cdot\exp^{\frac{23}{15}\cdot \pi\cdot i}&&\qquad(k=3)\\
&z_5&&=\sqrt[5]{6}\cdot\exp^{\frac{29}{15}\cdot \pi\cdot i}&&\qquad(k=4)
\end{alignat*}

Alle Lösungen von $z^5=6-3\sqrt{3}\cdot i$ in der komplexen Zahlenebene:

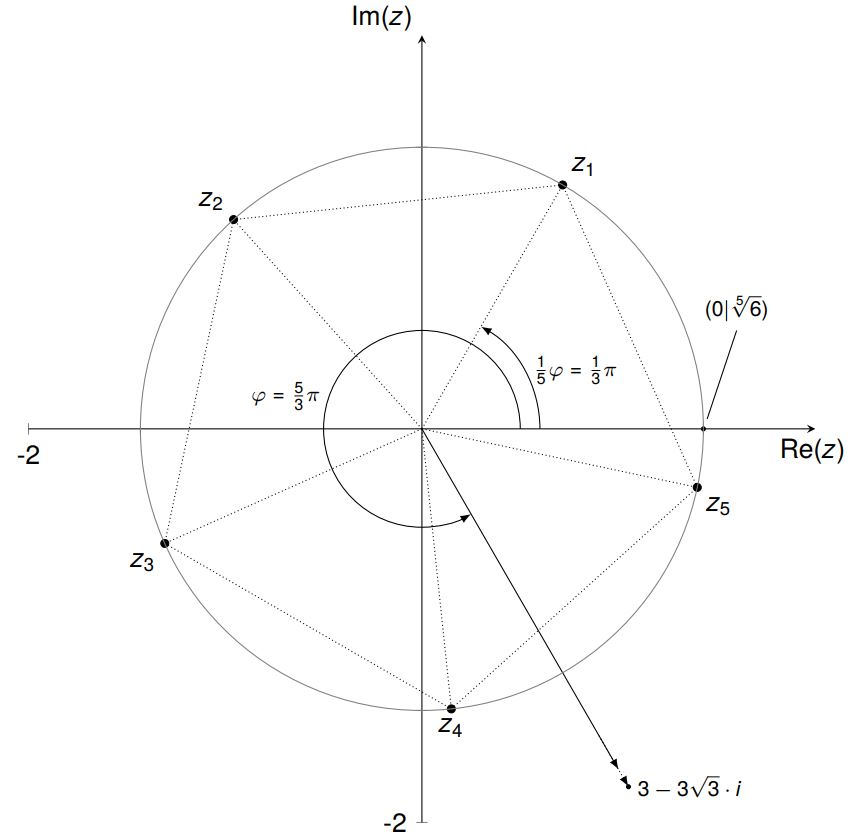
Es reicht theoretisch aus $z_1$ auszurechnen und sich $z_{2,\ldots,5}$ geometrisch zu konstruieren. Alle Lösungen $z_1 \textrm{ bis } z_5$ sind die Eckpunkte eines regelmäßigen Vielecks auf dem Kreis mit Radius $\sqrt[5]{6}$. Diese Anordnung erlaubt es uns die restlichen vier Lösungen neben $z_1$ zu bestimmen. Der Winkel ($\frac{2\pi}{5}$) zwischen allen Lösungen wird jeweils aufaddiert – mit $z_1$ als „Ausgangslösung“.

Also:

\begin{alignat*}{3}
&z^5&&=3-3\sqrt{3}\\
\Leftrightarrow\ &z^5&&=6\cdot\exp^{\frac{5}{3}\pi\cdot i}\\
&z_1&&=\sqrt[5]{6}\cdot\exp^{\frac{1}{5}\cdot\frac{5}{3}\pi\cdot i}=\sqrt[5]{6}\cdot\exp^{\frac{1}{3}\pi\cdot i}\\[4mm]
& &&\text{da 5. Wurzel: }\frac{2\pi}{5}\text{ von einer zur nächsten Lösung zum Argument add.:}\\[4mm]
\Rightarrow\ &z_2&&=\sqrt[5]{6}\cdot\exp^{\left(\frac{1}{3}\pi+\frac{2\pi}{5}\right)\cdot i}=\sqrt[5]{6}\cdot\exp^{\frac{11}{15}\pi\cdot i}\\
\Rightarrow\ &z_3&&=\sqrt[5]{6}\cdot\exp^{\left(\frac{11}{15}\pi+\frac{2\pi}{5}\right)\cdot i}=\sqrt[5]{6}\cdot\exp^{\frac{17}{15}\pi\cdot i}\\
\Rightarrow\ &z_4&&=\sqrt[5]{6}\cdot\exp^{\left(\frac{17}{15}\pi+\frac{2\pi}{5}\right)\cdot i}=\sqrt[5]{6}\cdot\exp^{\frac{23}{15}\pi\cdot i}\\
\Rightarrow\ &z_5&&=\sqrt[5]{6}\cdot\exp^{\left(\frac{23}{15}\pi+\frac{2\pi}{5}\right)\cdot i}=\sqrt[5]{6}\cdot\exp^{\frac{29}{15}\pi\cdot i}
\end{alignat*}

Ob du dir die Formel merkst, oder nach diesem Schema rechnest, ist natürlich dir selbst überlassen.

Potenzen von i und kombiniertes Beispiel

\begin{align*}
&\begin{array}{*4{>{\displaystyle}l}}
i^2=-1 &\quad,\,i^3=-i &\quad,\,i^4=(-1)^2=1 &\quad,\,i^{25}=i^{24}\cdot i=i\\
i^{79}=i^{76}\cdot i^3=-i &\quad,\,i^{568}=1 &\quad,\,i^{946}=i^{944}\cdot i^2=-1 &\quad,\,i^{-7}=\frac{1}{i^7}=\frac{i}{i^8}=i
\end{array}
\end{align*}

Eine Zahl ist durch 4 teilbar, wenn ihre letzten beiden Ziffern eine durch 4 teilbare Zahl ergeben.

Komplexe Folgen und Reihen

Wir wollen hier kurz das Thema „Konvergenzverhalten von komplexen Folgen und Reihen“ anreißen. Eine komplexe Folge oder Reihe ist dann konvergent, wenn ihr Real- und Imaginärteil konvergiert.

Die Grenzwertberechnung und der Nachweis von Konvergenz oder Divergenz von Folgen und Reihen funktioniert mit komplexen Zahlen genauso, wie mit reellen Zahlen. Die Anwendung der Konvergenzkriterien ist allerdings eingeschränkt. Es gibt kein Vergleichskriterium bei Folgen und kein Majoranten-, Minoranten- und Leibnizkriterium bei Reihen sowie allgemein keine Abschätzungen nach oben oder unten, da < und > bei komplexen Zahlen nicht existiert.

\begin{align*}
a_n = \frac{n+3i}{2n-i}\ ,\quad \lim\limits_{n\to \infty}{a_n} = \lim\limits_{n\to \infty}{\frac{n+3i}{2n-i}} = \lim\limits_{n\to \infty}{\frac{n\left(1+\frac{3i}{n}\right)}{n\left(2-\frac{i}{n}\right)}}=\frac{1}{2}
\end{align*}

\begin{align*}
b_n = \frac{n+3i}{2n-ni}\ ,\quad \lim\limits_{n\to \infty}{b_n} = \lim\limits_{n\to \infty}{\frac{n\left(1+\frac{3i}{n}\right)}{n\left(2-i\right)}}=\frac{1}{2-i}=\frac{1(2+i)}{4+1}=\frac{2}{5}+\frac{1}{5}i
\end{align*}

\begin{align*}
c_n = \left(\frac{3}{4}\cdot \text{e}^{i\pi}\right)^n\ ,\quad \lim\limits_{n\to \infty}{c_n} = \lim\limits_{n\to \infty}{\left(\frac{3}{4}\cdot \text{e}^{i\pi}\right)^n} = \lim\limits_{n\to \infty}{\left(\frac{3}{4}\right)^n\cdot \text{e}^{i\pi n}} = 0
\end{align*}

\begin{align*}
\sum_{k=0}^{\infty}&{\frac{(2+i)^k}{k!}}\ , \quad \left|\frac{a_{k+1}}{a_k}\right|=\left|\frac{\frac{(2+i)^{k+1}}{(k+1)!}}{\frac{(2+i)^k}{k!}}\right|=\left|\frac{(2+i)(2+i)^k\cdot k!}{k!(k+1)\cdot (2+i)^k}\right|=\left|\frac{2+i}{k+1}\right|\lim\limits_{k\to \infty} 0<1\\
&\Rightarrow \sum_{k=0}^{\infty}{\frac{(2+i)^k}{k!}}\text{ konvergiert (absolut).}
\end{align*}