
Kurvendiskussion
Auf dieser Seite findest du alles, was du zum Thema Kurvendiksussion wissen musst. Schritt für Schritt erklären wir dir anhand von ausführlichen Erklärungen folgende Themen:
Inhaltsverzeichnis
- Kurvendiskussion Grundlagen
- Extrempunkte (Hochpunkte & Tiefpunkte)
- Wendepunkte
- Monotonie
- Krümmung
- Grenzverhalten (Limes gegen +/- unendlich)
- Symmetrie
- Achsenabschnitte
- Einschub Intervallschreibweise
- Definitionsbereich
- Wertebereich
Kurvendiskussion Grundlagen
Übersicht von geometrischen Eigenschaften, die bei einer Kurvendiskussion untersucht werden können:
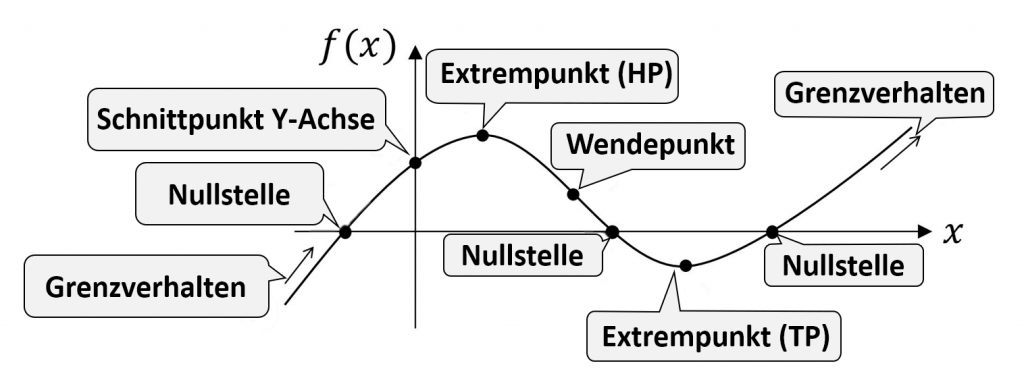
Zusätzlich werden wir folgende Themen untersuchen:
- Definitionsbereich
- Wertebereich
- Symmetrie
- Skizze (grob) – Zeichnung (genau)
Schau dir vertiefend Daniels Einführungsvideo zum Thema Kurvendiskussion an!
Extrempunkte (Hochpunkt & Tiefpunkt) berechnen
Vorgehen:
1. Notwendige Bedingung:
$f'(x)=0 \ \Rightarrow$ wir erhalten potentielle Extremstellen $x_E$!
2. Hinreichende Bedingung:
$f'(x_E)=0$ und $f“(x_E)\neq 0$
Für $f“(x_E)$ kann folgendes rauskommen:
- $f“(x_E)<0$ Hochpunkt (HP)
- $f“(x_E)=0$ Sattelpunkt (SP), für SP muss zudem $f“'(x_E)\neq 0$ sein!
- $f“(x_E)>0$ Tiefpunkt (TP)
3. y-Wert der Extremstelle:
$x_E$-Wert in $f(x)$ einsetzen $\Rightarrow$ $E(x_E/f(x_E))$
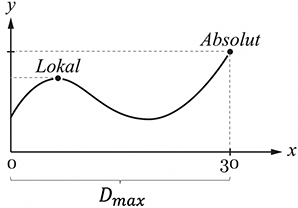
Achtung!
Es muss zwischen lokalen und globalen (oder absoluten) Extremstellen unterschieden werden! Stichwort: Randwerte!
Randwerte in $f(x)$ einsetzen und Ergebnis mit y-Wert vom Extrempunkt vergleichen! In dem obigen Bild sieht man, dass der höchste Punkt bei $x=30$ liegt und nicht beim errechneten Hochpunkt!
Merkt euch: Bei vorgegeben Intervall immer die Randwerte mit überprüfen!
Neu!
Beispiel zu Extrempunkten
Untersuche die Funktion $f(x)=\frac{2}{3}x^3+3x^2+4x$ mit $D = \mathbb{R}$ auf Extremstellen.
Schritt 1 Erste Ableitung bilden und gleich Null setzen:
$f'(x)=2x^2+6x+4=0$ liefert die möglichen Extremstellen $x_1=-2$ und $x_2=-1$.
Schritt 2 Zweite Ableitung bilden und Extremstellen einsetzen: $f“(x)=4x+6$.
$
\begin{array}{lcrclll}
f“(-2) & = &-2 & < 0 & \Rightarrow & Hochpunkt an der Stelle & x=-2 \\
f“(-1) & = &2 & >0 & \Rightarrow & Tiefpunkt an der Stelle & x=-1
\end{array}
$
Schritt 3 $y$-Wert des Hoch- und Tiefpunktes berechnen:
\begin{align*}
y=f(-2)=-\frac{4}{3} \quad \textrm{und} \quad y=f(-1)=-\frac{5}{3}
\end{align*}
Die Funktion f(x) besitzt einen Hochpunkt bei (-2|-4/3) und einen Tiefpunkt bei (-1|-5/3).
Schau dir zum Thema Extremwerte beide Videos von Daniel an!
Wendepunkte
Vorgehen:
1. Notwendige Bedingung: :
$f“(x)=0 \ \Rightarrow$ wir erhalten potentielle Wendestellen $x_W$!
2. Hinreichende Bedingung: :
$f“(x_W)=0$ und $f“'(x_W)\neq 0$
Für $f“'(x_W)$ kann folgendes rauskommen:
- $f“'(x_W)<0$ Links-rechts-Wendestelle
- $f“'(x_W)>0$ Rechts-links-Wendestelle
3. y-Wert der Wendestelle:
$x_W$-Wert in f(x) einsetzen $\Rightarrow$ $W(x_W/f(x_W))$
Graphisch betrachtet handelt es sich bei einem Wendepunkt um einen Punkt, an dem der Funktionsgraph sein Krümmungsverhalten ändert. Er wechselt an dieser Stelle entweder von einer Rechts- in eine Linkskurve oder umgekehrt. Hinweise, wann man den Wendepunkt berechnen soll sind, wenn:
- nach der stärksten Zunahme vom Graph
- nach der stärksten Abnahme vom Graph
gefragt ist.
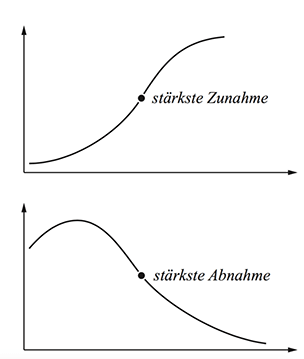
Schaut euch unbedingt den Abschnitt „Was ist in der Funktion gegeben?“ an.
Wenn $f(x)$ schon die Geschwindigkeit angibt und es wird nach der stärksten Zunahmegeschwindigkeit gefragt, dann benötigt man den Hochpunkt!
Auch hier wieder der Hinweis mit den Randwerten! Hier sollten bei einem vorgegeben Intervall in die 1. Ableitung Randwerte und $x$-Wert von WP eingesetzt werden. Das, was jeweils raus kommt (die Änderung/Zunahme bei positivem Wert oder Abnahme bei negativem Wert) mit errechneten Wendestellen vergleichen.
Neu!
Beispiel zu Wendepunkten
Untersuche die Funktion $f(x)=\frac{2}{3}x^3+3x^2+4x$ mit $D = \mathbb{R}$ auf Wendestellen.
Schritt 1: Zweite Ableitung bilden und gleich Null setzen: f“(x)=4x+6=0 liefert die mögliche Wendestelle x=-1,5.
Schritt 2: Dritte Ableitung bilden und Wendestellen einsetzen: $f“'(x)=4\neq 0$. Da in der dritten Ableitung kein x vorkommt, sind wir hier fertig, denn die dritte Ableitung ist immer ungleich Null! Es liegt ein Rechts-links Wendepunkt vor.
Schritt 3: y-Wert des Wendepunktes berechnen: y=f(-1,5)=-1,5.
Die Funktion f(x) besitzt einen Wendepunkt bei (-1,5|-1,5).
Schau dir die beiden Lernvideos von Daniel zum Thema Wendestellen an und vertiefe dein Wissen!
Monotonie
Zur Beurteilung des Monotonieverhaltens (Steigungsverhaltens) einer Funktion f(x) kann die Ableitung f'(x) betrachtet werden. Bekanntlich liefert die erste Ableitung einer Funktion f(x) die Steigungsfunktion f’(x), welche die an jeder Stelle x beschreibt, ob der Graph gerade steigt ($\nearrow$) oder fällt ($\searrow$). Damit lässt sich der Monotoniesatz wie folgt formulieren:

Streng monoton bedeutet hierbei, dass die Steigungsfunktion f'(x) an keiner Stelle x den Wert 0 annimmt!
Streng monoton steigend – Ableitung überall echt größer Null.
Monoton steigend – Ableitung überall größer oder gleich Null.
Das Ganze soll euch anhand des folgenden Beispiels klar werden.
Beispiel 1
Die Funktion
\begin{align*}
f(x)=\frac{1}{9}x^3 – \frac{1}{3}x^2 – \frac{8}{3} x + \frac{26}{9}
\end{align*}
soll mit Hilfe der ersten Ableitung auf ihr Monotonieverhalten untersucht werden.
Das allgemeine Vorgehen lässt sich so ungefähr beschreiben:
- Ableitung $f'(x)$ bilden.
- $f'(x)=0$ setzen und Nullstellen der Ableitungsfunktion bestimmen – hier: x=-2 und x=4.
- überprüfung, ob Werte der Ableitungsfunktion größer oder kleiner als 0 sind – indem wir Werte, die links und rechts von den Nullstellen liegen, in die Ableitungsfunktion einsetzen. So kann ein eventueller Vorzeichenwechsel – der auf eine änderung der Steigung hinweist – schnellstens entdeckt werden. Hier zum Beispiel so: $f'(x=-3); \ f'(x=0);\ f'(x=5)$. Man kann aber auch andere Werte einsetzen – aber nicht die Nullstellen!
Das Monotonieverhalten Lernvideo von Daniel hilft dir nochmals das Thema zu verstehen!
Krümmung
Zur Beurteilung der Krümmung verwendet man häufig die zweite Ableitung. Es gilt
\begin{align*}
&f“(x) > 0 \quad \Rightarrow \quad f(x) \ \textrm{ist links gekrümmt bzw. konvex} \ \cup \\
&f“(x) < 0 \quad \Rightarrow \quad f(x) \ \textrm{ist rechts gekrümmt bzw. konkav} \ \cap \end{align*}
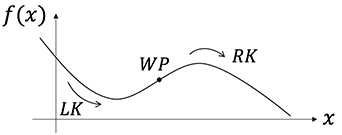
Das ganze soll euch anhand des folgenden Beispiels klar werden. Die Funktion \begin{align*} f(x)=x^2, \quad x \in \mathbb{R} \end{align*} soll mit Hilfe der zweiten Ableitung auf ihr Krümmungsverhalten untersucht werden. Wir bilden zunächst die zweite Ableitung \begin{align*} f'(x)=2x \quad \Rightarrow \quad f“(x)=2>0
\end{align*}
und sehen, dass die zweite Ableitung stets größer als 0 und damit linksgekrümmt bzw. konvex ist.
Daniel erklärt euch das Krümmungsverhalten einer Funktion nochmals per Video!
Wer mehr über die Konvexität einer Funktion erfahren möchte findet das in diesem Lernvideo von Daniel.
Grenzverhalten (limes)
- $\lim\limits_{x \to -\infty}$ „ich schaue links“ – hohe negative Zahl für $x$ einsetzen = „Wo kommt der Graph her?“
- $\lim\limits_{x \to +\infty}$ „ich schaue rechts“ – hohe positive Zahl für $x$ einsetzen = „Wo geht der Graph hin?“
- Verhalten für $x \to \pm \infty$
- Schauen wir uns einmal folgende Funktion an: $f(x)= a_n \cdot x^n$. Zur Beurteilung des Verhaltens betrachtet man immer die höchste Potenz $n$ von $x$ und ihren Koeffizienten $a_n$:
- Wenn $n$ gerade und $a_n>0$ ist, so strebt $f(x) \to + \infty$ für $x \to \pm \infty$.
- Wenn $n$ gerade und $a_n<0$ ist, so strebt $f(x) \to – \infty$ für $x \to \pm \infty$.
- Wenn $n$ ungerade und $a_n>0$ ist, so strebt $f(x) \to + \infty$ für $x \to + \infty$ und $f(x) \to – \infty$ für $x \to – \infty$.
- Wenn $n$ ungerade und $a_n<0$ ist, so strebt $f(x) \to – \infty$ für $x \to + \infty$ und $f(x) \to + \infty$ für $x \to – \infty$.
Lass dir das Thema Grenzverhalten nochmals von Daniel erklären!
Symmetrie
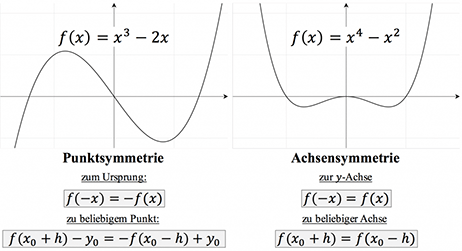
Symmetrieeigenschaften bei ganzrationalen Funktionen:
- Kommen in der Funktion nur gerade Exponenten vor, wie z.B. bei\begin{align*}
f(x)=x^4-2x^2-4
\end{align*}dann ist die Funktion achsensymmetrisch zur y-Achse! Wir können die Achsensymmetrie zur y-Achse auch rechnerisch zeigen. Es gilt\begin{align*}
f(-x)&=f(x) \\
(-x)^{4}-2 \cdot(-x)^{2}-4 &= x^{4}-2 x^{2}-4 \\
x^{4}-2 x^{2}-4 &= x^{4}-2 x^{2}-4 \quad
\end{align*} - Kommen in der Funktion nur ungerade Exponenten vor, wie z.B. bei\begin{align*}
f(x)=2x^3-4x
\end{align*}dann ist die Funktion punktsymmetrisch zum Ursprung. Wir können die Punktsymmetrie zum Ursprung auch rechnerisch zeigen. Es gilt\begin{align*}
f(-x)&=-f(x) \\
2\cdot (-x)^3-4 \cdot (-x) &=-(2x^3-4x) \\
-2x^3+4x &= -2x^3+4x \quad
\end{align*}
- Eine Funktion f(x) ist zu einer zweiten Funktion g(x) achsensymmetrisch bzgl. der x-Achse, wenn gilt: f(x)=-g(x)
Neu!
Daniel erklärt dir in seinem Lernvideo nochmal alles zur Symmetrie bei Funktionen
Achsenabschnitte
Hier werden die Achsenabschnitte
- mit der y-Achse untersucht:
Gegeben sei eine Funktion $f(x)=2x^2-4x-16$. Für den y-Achsenabschnitt setzen wir x=0 in die Funktion ein
\begin{align*}
f(x)&=2x^2-4x-16 \\
f(0)&= 2\cdot 0^2-4\cdot 0 -16 \\
f(0)&=-16
\end{align*}
und wir erhalten mit $S_y(0/-16)$ den Schnittpunkt von Funktion und y-Achse.
- mit der $x$-Achse untersucht:Der Schnittpunkt mit der x-Achse wird auch Nullstelle genannt.
Hierfür setzen wir unsere gegebene Funktion f(x)=0.
Mit der Funktion von oben folgt für dieNullstellen:\begin{align*}
f(x)&=0 \\
2x^2-4x-16 &=0 \quad |:2 \ \textrm{PQ-Formel} \\
x_1=-2 \ &\wedge \ x_2=4.
\end{align*}
Daniel erklärt dir nochmal das Thema Achenschnittpunkte in seinem Lernvideo
Einschub Intervallschreibweise
\begin{array}{l|l|c}
Schreibweise & Mengenschreibweise & Typ \\ \hline
[a,b] & \{x \in \mathbb{R} \mid a \leq x \leq b \} & geschlossen \\
[a,b) & \{x \in \mathbb{R} \mid a \leq x < b \} & halb-offen \\
(a,b] & \{x \in \mathbb{R} \mid a < x \leq b \} & halb-offen \\
(a,b) & \{x \in \mathbb{R} \mid a <x <b \} & offen
\end{array}
Die Intervallschreibweise ist eine abkürzende Schreibweise und wird oft beim Definitions- und Wertebereich verwendet. Das Intervall gibt an, in welchem Bereich sich unser x befindet. Zum Beispiel können wir $2\leq x < 4$ abkürzend als [2;4) schreiben.
Daniel erklärt dir alles rund um die Intervallschreibweise.
Definitionsbereich
Die Bestimmung des Definitionsbereichs ist sehr wichtig. Auch wenn oft in der Aufgabenstellung nicht explizit gefordert,
sollte man sich bevor man irgendetwas rechnet immer vergewissern, welche x-Werte man in die Funktion f(x) überhaupt einsetzen darf.
Wenn der Definitionsbereich schon vorgegeben ist, müsst ihr diesen verwenden.
Die 3 Warnschilder bei der Bestimmung des maximalen Definitionsbereiches:
- $\frac{1}{\textrm{etwas}}$ verlangt etwas $\neq 0$
- $\sqrt{\textrm{etwas}}$ verlangt etwas $\geq 0$
- $\ln(\textrm{etwas})$ verlangt etwas $>0$
Beachte: Der Definitionsbereich D kann sich beim Ableiten verändern!
Beispiel zum Definitionsbereich
Bestimme den maximalen Definitionsbereich der Funktion $f(x)= \frac{\sqrt{x^2}}{\ln(2-x)}$.
Zufälligerweise kommen in der Funktion Logarithmus, Bruch und Wurzel vor! Alarmglocken gehen an. Alle drei Bedingungen von oben werden geprüft.
\begin{align*}
\quad \frac{1}{\textrm{etwas}} \quad \textrm{verlangt} \quad \textrm{etwas} \neq 0 \ \Rightarrow \ln(2-x) &\neq 0 \quad |e^{\wedge} \\
2-x&\neq e^0 \\ 2-x &\neq 1 \quad |+x \ -1 \\
x &\neq 1
\end{align*}
Wir wissen jetzt schon mal, dass unser x nicht 1 sein darf. Weiter geht es mit Prüfung der Wurzel! Der Radikand (die Zahl unter der Wurzel) darf nie kleiner als Null sein.
\begin{align*}
\quad \sqrt{\textrm{etwas}} \quad \textrm{verlangt} \quad \textrm{etwas} \geq 0 \ \Rightarrow \ x^2 &\geq 0 \\ \Leftrightarrow \quad -\infty < x &< \infty \end{align*}
Egal was wir für $x$ einsetzen, durch das $x^2$ kommt immer eine Zahl raus, die größer oder gleich 0 ist. Wir dürfen also für $x$ alle Zahlen von – bis + Unendlich einsetzen. Abschließend folgt die Prüfung des Logarithmus.
\begin{align*} 3. \quad \ln(\textrm{etwas}) \quad \textrm{verlangt} \quad \textrm{etwas} > 0 \ \Rightarrow 2-x &> 0 \quad |+x \\
2 > x \ \Leftrightarrow \ x&
\end{align*}
Für den Definitionsbereich von $f(x)$ müssen alle Bedingungen, die geprüft wurden, erfüllt sein. Welche $x$-Werte erfüllen alle 3 Bedingungen? Am Einfachsten kann man sich das am Zahlenstrahl klar machen.
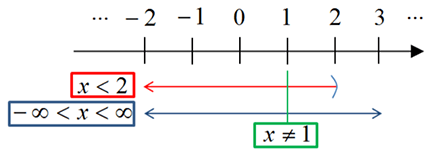
Der maximale Definitionsbereich für die Funktion f(x) lautet demnach
\begin{align*}
D_f = \underbrace{(-\infty,1) \cup (1,2)}_{\textrm{Intervallschreibweise}} = \left\{x \in \mathbb{R} | x<1 \vee 1<x<2 \right\}.
\end{align*}
Schau dir vertiefend zum Thema Definitionsbereich nochmal Daniels Lernvideo an.
Wertebereich
Der Wertebereich W ist die Menge von y-Werten, die du erhältst, wenn du jedes mögliche x in die Funktion $f(x)$ einsetzt. Anders gesagt: Alles, was für y rauskommen kann! Betrachten wir den Wertebereich des folgenden Graphen:
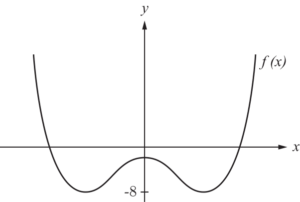
\begin{align*}
W = [-8;\infty)
\end{align*}
Hierbei ist -8 der niedrigste y-Wert, der erreicht wird. Nach oben gibt es jedoch keine Begrenzung; es kann jeder positive y-Wert angenommen werden. Nach dem Wertebereich wird selten bis nie gefragt. Wichtig ist bei Anwendungsaufgaben den Blick für „Höhen“/“Tiefen“ zu haben!
Schau dir zu dem Thema Werebereich das passende Video von Daniel an“

