
Lineare Funktionen
In diesem Artikel erfährst du alles über lineare Funktionen. Wir behandeln folgende Themen:
- Was sind lineare Funktionen?
- Steigung einer linearen Funktion berechnen
- Nullstelle einer linearen Funktion berechnen
- Beispielaufgaben zu Lineare Funktionen
Was sind Lineare Funktionen?
Lineare Funktionen sind euch wahrscheinlich ebenfalls unter dem Namen Geradengleichungen bekannt. Der Name sagt also schon, um was für eine Art Graph es sich in diesem Fall handelt, nämlich um eine Gerade. Wir halten demnach fest, dass Graphen von linearen Funktionen sich im Koordinatensystem ausschließlich als eine Gerade darstellen lassen. Im Allgemeinen haben lineare Funktionen immer die folgende Gestalt:
\[y=m\cdot x+b\]
Wir notieren, dass $m$ die Steigung und $b$ den Schnittpunkt der Geraden mit der $y$-Achse angibt. Beachte: Im Regelfall werden Funktionen immer $f(x)$ genannt. $f(x)$ ist nichts anders als der Funktionswert, also $y$.
Nachfolgend betrachten wir den Graphen der linearen Funktion $y=f\left(x\right)=2x-1$ im Koordinatensystem:
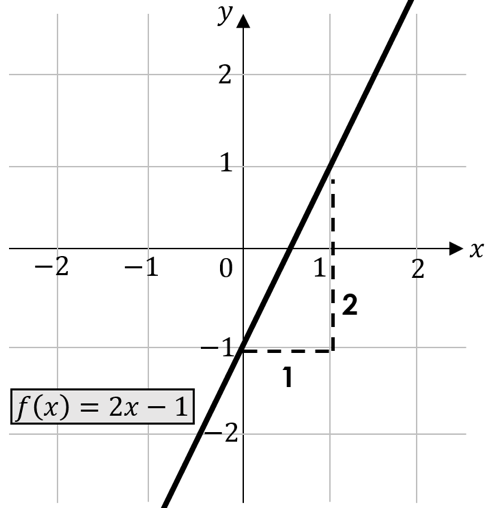
Der Graph der Funktion $f\left(x\right)=2x-1$ schneidet die $y$-Achse im Punkt $(0|-1)$. Punkte werden immer in der Form ( $x$-Wert | $y$-Wert) dargestellt.
Wir halten an dieser Stelle also fest, dass Schnittpunkte mit der $y$-Achse immer die $x$-Koordinate $0$ haben. Dazu stellen wir uns vor, dass wir den Punkt $(0|-1)$ im Koordinatensystem ausfindig machen wollen.
Wir beginnen im Ursprung, also im Punkt $(0|0)$. Von da aus gehen wir immer zuerst in $x$-Richtung, also nach links oder nach rechts. In unserem Fall müssen wir uns weder nach links noch nach rechts bewegen, um zu unserem gewollten Punkt zu gelangen. Anschließend bewegen wir uns in -Richtung, als entweder nach oben oder nach unten. Hier gehen wir eine Einheit nach unten und landen genau auf unserem Punkt $(0|-1)$.
Von unserem Schnittpunkt mit der $y$-Achse aus wollen wir nun unser Steigungsdreieck einzeichnen. Merkt euch, dass sich Steigungen immer als Quotient $\frac{y}{x}$ angeben lassen. Wir gehen, wie in der Grafik zu sehen, eine Einheit nach rechts und 2 Einheiten nach oben und gelangen zu einem weiteren Punkt auf unserer Geraden $(\frac{y}{x}=\frac{2}{1} =2)$. In unserem Fall war die Steigung $m=2$ positiv.
Es kann natürlich auch vorkommen, dass unsere Steigung einen negativen Wert annimmt. Dazu gucken wir uns einen weiteren Graphen im Koordinatensystem an:
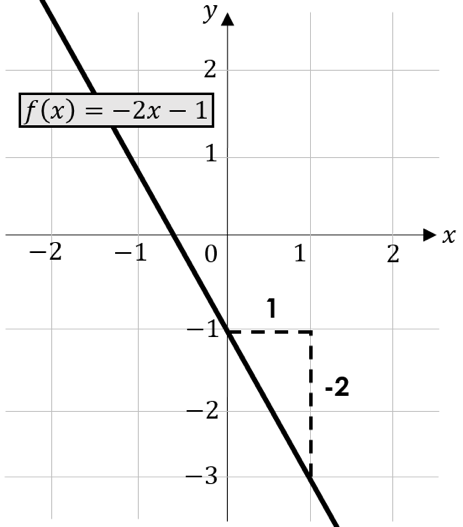
Die Funktion $f\left(x\right)=-2x-1$ hat die Steigung $m=-2$. Jetzt müssen wir von unserem Schnittpunkt mit der $y$-Achse aus wieder eine Einheit nach rechts gehen aber anschließend gehen wir 2 Einheiten nach unten, da unsere Steigung jetzt negativ ist.
Wir merken uns also für lineare Funktionen:
- Positive Steigung: $x$ Einheiten nach rechts und $y$ Einheiten nach oben, z.B. $m=$ $\frac{3}{4}$: $4$ Einheiten nach rechts und $3$ Einheiten nach oben
- Negative Steigung: $x$ Einheiten nach links und $y$ Einheiten nach unten, z.B. $m=-$ $\frac{3}{1}$: $1$ Einheiten nach rechts und $3$ Einheiten nach unten
Steigung einer linearen Funktion berechnen
Mit der Punkt-Steigungs-Form ist es möglich aus zwei gegebenen Punkten eine Funktionsgleichung aufzustellen. Wir nehmen an, dass die beiden folgenden Punkte gegeben sind: $P(2|-3)$ und $Q(1|2)$. Zu Anfang benötigen wir die folgende Formel zur Berechnung der Steigung:
\[m=\frac{y_2-y_1}{x_2-x_1}\]
Die $y$-Koordinate unseres Punktes $Q$ ist $y_2=2$, die $y$-Koordinate unseres $P$ ist $y_1=-3$, die $x$-Koordinate unseres Punktes $Q$ ist $x_2=1$ und die $x$-Koordinate unseres Punktes $P$ ist $x_1=2$. Diese Werte setzen wir jetzt in unsere obige Formel ein und erhalten:
\[m=\frac{y_2-y_1}{x_2-x_1}=\frac{2-(-3)}{1-2}=\frac{2+3}{-1}=\frac{5}{-1}=-5\]
Unsere Steigung ist also $m=-5$.
Hinweis: Ihr bekommt das gleiche Ergebnis, wenn ihr für die $x_1$ und $y_1$-Koordinaten die Werte von Punkt Q nehmt und ihr für die $x_2$ und $y_2$-Koordinaten die Werte von Punkt P.
\[m=\frac{y_2-y_1}{x_2-x_1}=\frac{\left(-3\right)-2}{2-1}=\frac{-5}{1}=-5\]
Im nächsten Schritt setzen wir sowohl unsere eben berechnete Steigung als auch die beiden Koordinaten einer der beiden Punkte in unsere allgemeine Funktionsgleichung $y=m\cdot x+b$ ein. Dabei spielt es keine Rolle, ob ihr euch für den Punkt $P$ oder den Punkt $Q$ entscheidet. Beide Einsetzungen liefern ein identisches Ergebnis. Wir entscheiden uns jetzt für den Punkt $Q$ und erhalten:
\[2=-5\cdot 1+b\]
Diese Gleichung lösen wir jetzt nach $b$ auf:
\[2=-5+b |+5\]
\[2+5=b\]
\[7=b\]
Damit hätten wir sowohl unsere Steigung $m$ als auch unseren Schnittpunkt mit der $y$-Achse $b$ berechnet und können jetzt unsere Funktionsgleichung aufschreiben. Diese lautet dann:
\[y=-5\cdot x+7\]
Nullstellen berechnen – Lineare Funktionen
Was sind Nullstellen?
Nullstellen sind der oder die Schnittpunkte des Graphen der Funktion mit der $x$-Achse. Grundsätzlich gilt, dass man zur Berechnung der Nullstellen den Funktionsterm gleich 0 setzen muss. Diese Tatsache ist nicht nur für lineare Funktionen, sondern auch für jede andere Funktionsart (z.B. quadratische Funktionen) gültig. Merkt euch, dass Geraden maximal eine Nullstelle besitzen können. Wir möchten jetzt beispielhaft die Nullstellen unserer zuvor berechneten Geraden bestimmen. Also erhalten wir, nach dem wir unseren Funktionsterm gleich 0 gesetzt haben:
\[0=-5\cdot x+7\]
Diese Gleichung lösen wir jetzt nach $x$ auf:
\[0=-5\cdot x+7 |-7\]
\[-7=-5\cdot x |\div (-5)\]
\[1,4=x\]
Unsere Gerade schneidet die $x$-Achse an der Stelle $x=1,4$. Das ist die einzige Nullstelle.
Merkt euch, dass Schnittpunkte mit der $x$-Achse immer die folgende Gestalt haben: $(x|0)$, in unserem Beispiel also $\left(1,4\ \right|\ 0)$.
Parallele Geraden zur $x$– und $y$-Achse
Zu Beginn gucken wir uns die beiden folgenden Geraden im Koordinatensystem an:
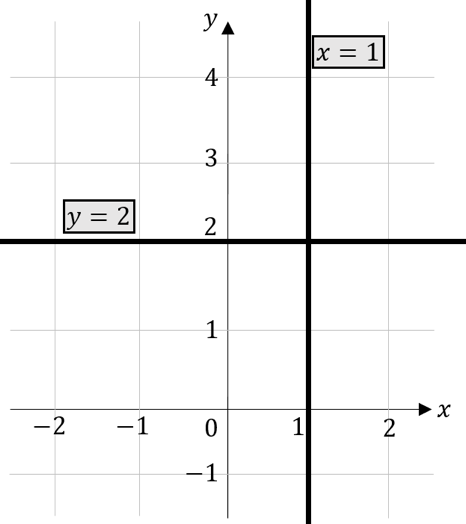
Wir sehen zwei Geraden, zum einen $y=2$ und zum anderen $x=1$. Parallele Geraden zur $x$-Achse geben immer an, an welcher Stelle die $y$-Achse geschnitten wird. Parallele Geraden zur $y$-Achse geben immer an, an welcher Stelle die $x$-Achse geschnitten wird. Merkt euch, dass parallele Geraden zur $y$-Achse keinen Graphen einer linearen Funktion darstellen. Es werden nämlich einem $x$-Wert, mehrere $y$-Werte zugeordnet.
Beispielaufgabe – Lineare Funktionen
Ein Segelflugzeug befindet sich in $1200m$ Höhe. Beim Sinkflug verliert es pro Minute $40m$ an Höhe.
- a) Stelle eine geeignete Funktionsgleichung auf, welche den Sinkflug des Segelflugzeuges beschreibt.
- b)Nach wie vielen Minuten hat das Flugzeug den Erdboden erreicht?
Lösung zu a)
\begin{align*}
f(x) = 1200 – 40 \cdot x
\end{align*}
Unser Flugzeug hat eine anfängliche Höhe von $1200m$. Das $x$ steht hier für die Anzahl der Minuten, in welchen das Flugzeug jeweils $40m$ an Höhe verliert. $f(x)$ gibt die verbleibende Höhe nach $x$ Minuten an.
Lösungzu b)
Wir sollen herausfinden, nach wie vielen Minuten sich das Flugzeug wieder am Boden befindet. Die verbleibende Höhe $f(x)$ soll also gleich $0$ sein. Wenn wir diese Information in unsere Ausgangsgleichung einsetzen, erhalten wir:
\begin{align*}
0 = 1200 – 40 \cdot x
\end{align*}
Diese Gleichung lösen wir jetzt nach $x$ auf:
\begin{align*}
\begin{array}{rrcll}
& 0 & =&1200 – 40 \cdot x &|+40 \cdot x \\
\Leftrightarrow & 40 \cdot x &=&1200 &|:40 \\
\Leftrightarrow & x &=& 30
\end{array}
\end{align*}
Das Flugzeug befindet sich nach exakt einer halben Stunde wieder am Boden.
NEU
