Körper in der Mathematik

Im folgenden Artikel erklären wir dir alles Wichtige zum Thema Mathematische Körper. Du kannst im folgenden den gewünschten Körper auswählen:

Würfel
Quader
Pyramide
Zylinder
Kegel
Kugeln
Beispielaufgaben

Daniel erzählt euch alles zum Thema „Mathematische Körper“

Würfel

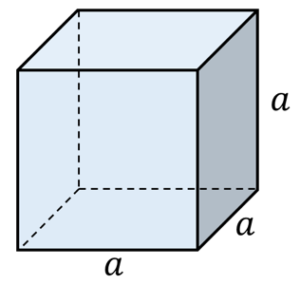
bil_wuerfel

Eigenschaften:

alle Kanten sind gleich lang
alle 6 Flächen sind gleich groß

Formeln:

Oberflächeninhalt: $O = 6 \cdot a^{2}$
Volumen: $V = a \cdot a \cdot a = a^{3}$

Quader

bil_quader

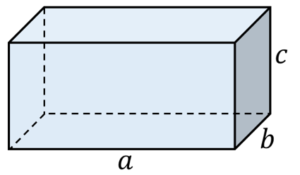
Formeln:

Oberflächeninhalt: $O = 2 \cdot a \cdot b + 2 \cdot a \cdot c + 2 \cdot b \cdot c = 2 \cdot (a \cdot b + a \cdot c + b \cdot c)$
Volumen: $V = a \cdot b \cdot c$

Pyramide (quadratisch)

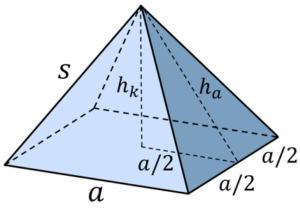
bil_pyramide

Formeln:

Oberflächeninhalt: $O = a^{2} + 2 \cdot a \cdot h_{a}$
Volumen: $V = \frac{1}{3} \cdot a^{2} \cdot h_{k} = \frac{1}{3} \cdot G \cdot h_{k}$

Außerdem gelten nach dem Satz des Pythagoras die folgenden Zusammenhänge:
${(\frac{a}{2})}^{2} + h_{k}^{2} = h_{a}^{2}$ und ${(\frac{a}{2})}^{2} + h_{a}^{2} = s^{2}$

Zylinder

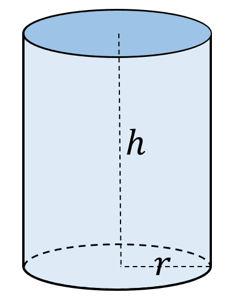
bil_zylinder

Formeln:

Oberflächeninhalt: $O = 2 \cdot π \cdot r^{2} + 2 \cdot π \cdot r \cdot h$
Mantelfläche: $M = 2 \cdot π \cdot r \cdot h$
Volumen: $V = π \cdot r^{2} \cdot h = G \cdot h$

Kegel

bil_kegel

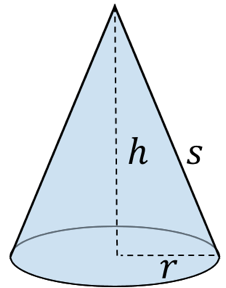
Formeln:

Oberflächeninhalt: $O = π \cdot r \cdot (r + s)$
Mantelfläche: $M = r \cdot s \cdot π$
Volumen: $V = \frac{1}{3} \cdot π \cdot r^{2} \cdot h = \frac{1}{3} \cdot G \cdot h$

Außerdem gilt nach dem Satz des Pythagoras der folgende Zusammenhang:
$r^{2} + h^{2} = s^{2}$

Kugel

bil_kugel

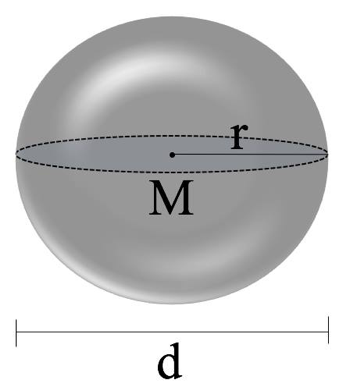
Formeln:

Oberflächeninhalt: $O = 4 \cdot π \cdot r^{2}$
Volumen: $V = \frac{4}{3} \cdot π \cdot r^{3}$

Beispielaufgaben

Volumen eines Würfels

Ein Würfel hat ein Volumen von $64 c m^{3}$ . Wie groß ist seine Oberfläche?

Lösung

Die Oberfläche eines Würfels wird mit der folgenden Formel berechnet:

$\begin{array}{r} O = 6 \cdot a^{2} \end{array}$

Es wird also die Grundkantenlänge des Würfels benötigt. Dazu wird das in der Aufgabe gegebene Volumen in die Volumenformel für einen Würfel eingesetzt:

$\begin{array}{r} V = a^{3} \Leftrightarrow 64 = a^{3} \end{array}$

Um die Grundkantenlänge bestimmen zu können, muss jetzt die dritte Wurzel aus $64$ gezogen werden:

$\begin{array}{r} 64 = a^{3} \to a = \sqrt[3]{64} = 4 c m \end{array}$

Zum Schluss wird jetzt noch der eben berechnete Wert in die Oberflächenformel eingesetzt:

$\begin{array}{r} O = 6 * 4^{2} = 96 c m^{2} \end{array}$

Der Würfel hat einen Oberflächeninhalt von $96 c m^{2}$ .

Mathe einfach erklärt! Unsere Lernhefte für die 5. bis 10. Klasse

4,5 von 5 Sternen

Im Shop ansehen

Mathe Vorbereitung für die 5. bis 10. Klasse

NEU

Beispielaufgabe Volumen eines Brunnens

Der Marktplatz in Paderborn soll einen neuen Brunnen bekommen. Unterhalb ist eine vorläufige Bauskizze zu sehen:

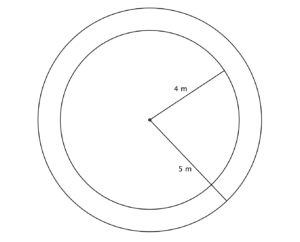
Volumen eines Brunnen

Lediglich der innere Teil des Brunnens soll mit Wasser gefüllt sein. Der Brunnen wird eine Wassertiefe von Wie viel Liter Wasser fasst der Brunnen?
Der äußere Ring soll den Bürgern als Sitzmöglichkeit zur Verfügung stehen. Wie groß ist die Fläche, welche zukünftig als Sitzgelegenheit zur genutzt werden kann?

Lösungen:

Aufgabenteil 1:

Es wird das Volumen des Brunnens in Litern gesucht. Mathematisch gesehen, handelt es sich bei diesem Körper um einen Zylinder. Das Volumen eines Zylinders wird mit der folgenden Formel berechnet:

$\begin{array}{r} V = π \cdot r^{2} \cdot h \end{array}$

Der Radius beträgt laut Skizze $? = 4 m$ und die Höhe laut Aufgabentext $h = 0, 5 ?$ . Nun werden die beiden Werte in die Volumenformel eingesetzt:

$\begin{array}{r} V = π \cdot 4^{2} \cdot 0, 5 \approx 25, 1 m^{3} \end{array}$

Anschließend muss das Ergebnis noch in der Einheit Liter angegeben werden. Dazu muss man den folgenden Zusammenhang kennen:

$\begin{array}{r} 1 l = 1 d m^{3} \end{array}$

Die $25, 1 m^{3}$ müssen also in $d m^{3}$ bzw. Liter umgewandelt werden:

$\begin{array}{r} 25, 1 m^{3} = 25100 d m^{3} (ℓ) \end{array}$

Der Brunnen fasst also $25100 ℓ$ Wasser.

Aufgabenteil 2:

Es wird der Flächeninhalt des äußeren Kreisringes gesucht. Grundsätzlich wird die Fläche eines Kreisringes mit der folgenden Formel berechnet:

$\begin{array}{r} A = π \cdot (r_{2}^{2} - r_{1}^{2}) \end{array}$

$r_{2}$ steht für den äußeren Radius und $r_{1}$ für den inneren Radius. Wir setzen beide Radien in die obige Formel ein und erhalten:

$\begin{array}{r} A = π \cdot (5^{2} - 4^{2}) \approx 28, 3 m^{2} \end{array}$

Die Größe der Sitzfläche beträgt circa $28, 3 m^{2}$ .

Mathe einfach erklärt! Unsere Lernhefte für die 5. bis 10. Klasse

4,5 von 5 Sternen

Im Shop ansehen

NEU