
Sekante, Tangente und Normale
Themen auf dieser Seite:
Sekantengleichung aufstellen
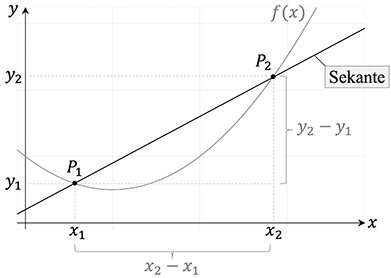
Die Sekante schneidet eine Funktion $f(x)$ in zwei Punkten. Im Sachzusammenhang gesehen beschreibt die Steigung der Sekante die durchschnittliche Änderung in einem Bereich, der durch die Schnittpunkte $P_1$ und $P_2$ der Geraden mit der Funktion gegeben ist.
Zur Erinnerung: $m=\frac{y_2-y_1}{x_2-x_1}$ bzw. $m =\frac{f(x_2)-f(x_1)}{x_2-x_1}$
Was ist in der Regel gegeben?
- Funktion, hier $f(x)=3x^2+1 $
- zwei Punkte oder 2 $x$-Werte, hier $P_1(-1|f(-1))$, $P_2(2|f(2))$
Vorgehen:
- Allgemeine Geradengleichung: $y=mx+b$ – Wir suchen also $m$ und $b$!
- Für $m$: Steigung durch zwei Punkte $m=\frac{y_2-y_1}{x_2-x_1}$
- Für $b$: $m$ und einen der beiden Punkte in allgemeine Geradengleichung einsetzen.
Für unser Beispiel wird die Sekantengleichung wie folgt berechnet:
\begin{align*}
y&=m \cdot x+b \quad \textrm{mit} \quad m=\frac{(3\cdot 2^2+1)-(3\cdot 1^2+1)}{2-(-1)}=\frac{9}{3}=3 \ \textrm{und} \ P_2(2|13) \\
\Rightarrow \quad 13&= 3 \cdot 2 + b \quad |-6 \quad \Leftrightarrow \quad b= 7
\end{align*}
Die gesuchte Sekantengleichung lautet $y=3x+7$.
Schau dir zur Vertiefung Daniels Lernvideo zu dem Thema an!
Tangentengleichung aufstellen
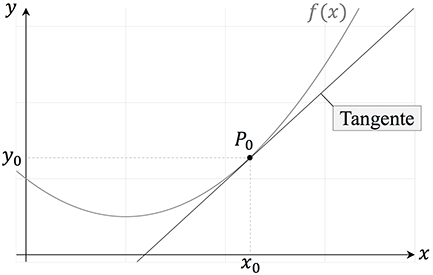
Die Tangente berührt eine Funktion $f(x)$ in einem Punkt $P_0$. Die Steigung der Tangente $m_{tan}$ beschreibt die Steigung in einem beliebigen Punkt $x_0$.
Im Sachzusammenhang gesehen beschreibt die Steigung die momentane Änderung.
Zur Erinnerung:
\begin{align*}
m_{tan}=f'(x_0)
\end{align*}
Was ist in der Regel gegeben?
- Funktion, hier $f(x)=3x^2+1 $
- $x$-Wert, hier $P(1/f(1))$
Vorgehen:
- Allgemeine Geradengleichung gesucht: $y=m \cdot x+b$ – Wir suchen also $m$ und $b$!
- Ableitung bestimmen $f'(x)$ , hier $f'(x)=m=6x$
- für $y$: $x$-Wert in $f(x)$ einsetzen, hier $f(1)=3 \cdot 1^2+1 \Rightarrow y=4$
- für $m$: $x$-Wert in $f'(x)$ einsetzen, hier $f'(1)=6 \cdot 1 \Rightarrow m=6$
- für $b$: $m$ und $y$ in allgemeine Geradengleichung einsetzen.
Für unser Beispiel folgt:
\begin{align*}
y&=m \cdot x+b \\
\Leftrightarrow \quad 4&= 6 \cdot 1 + b \\
\Leftrightarrow \quad 4&=6+b \quad |-6 \quad \Rightarrow \quad b= -2
\end{align*}
Die gesuchte Tangentengleichung lautet: $y=6x-2$
Normale, Senkrechte bzw. Orthogonale
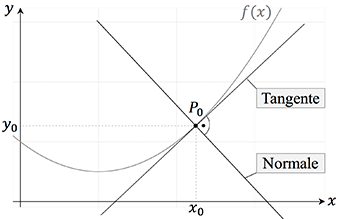
Die Ableitung einer Funktion $f(x)$ an einem Punkt $P_0$ ist gleich der Steigung der Tangente $m_{tan}$ an diesem Punkt. Die Normale verläuft senkrecht (othogonal) zur Tangente an diesem Berührungspunkt. Ihre Steigung ist der negative Kehrwert der Steigung der Tangente.
Wie wir bereits kennengelernt haben, wird die Steigung der Tangente durch
\begin{align*}
m_{tan}=f'(x_0)
\end{align*}
bestimmt. Die Steigung der Normalen lautet demnach:
\begin{align*}
m_{norm}=-\frac{1}{m_{tan}}=-\frac{1}{f'(x_0)}
\end{align*}
Neu!
Was ist in der Regel gegeben?
- Funktion, hier $f(x)=3x^2+1 $
- $x$-Wert, hier $P(1|f(1))$
Vorgehen:
- Allgemeine Geradengleichung gesucht: $y=m \cdot x+b$
- Ableitung $f'(x)$ und Steigung der Tangente $m_{tan}$ bestimmen, hier $f'(1)=6=m_{tan}$
- Steigungen der Normalen bestimmen, hier $m_{norm}=-1/m_{tan}=-1/6$
- für $b$: $m_{norm}$ und $P(1|4)$ in Geradengleichung einsetzen
Für unser Beispiel folgt:
\begin{align*}
y&=m \cdot x+b \\
\Rightarrow \quad 4&= -\frac{1}{6}\cdot 1 + b \quad |+\frac{1}{6} \quad \Rightarrow b = \frac{25}{6}
\end{align*}
Die gesuchte Normalengleichung lautet: $y=-\frac{1}{6}x+\frac{25}{6}$
Ganz wichtig: Es muss immer $m_{tan}\cdot m_{norm}=-1$ gelten!
Schau dir zur Vertiefung Daniels Playlist zu dem Thema an!

