Specials
Inhaltsverzeichnis
- Geraden in besonderer Lage
- Mehrfache Nullstellen
- Achsenabschnittsweise/Sückweise definierte Funktionen
- Abstand von zwei Punkten
- Senkrechter Abstand zweier Funktionen
- Winkel zwischen einer Geraden und x-Achse
- Winkel zwischen zwei Geraden
- Quadranten
Geraden in besonderer Lage
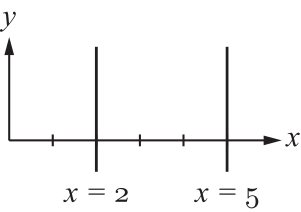
Parallelen zur $y$-Achse.
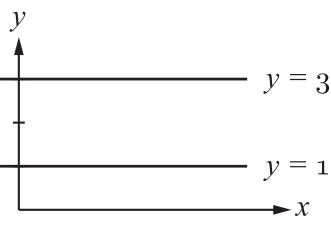
Parallelen zur $x$-Achse.
Daniel erklärt dir alle Sonderfälle in diesem Video!
Mehrfache Nullstellen
Doppelte Nullstelle
\begin{align*}
0&=\frac{1}{12}x^4-\frac{3}{2}x^2 \\
0&=x^2(\frac{1}{12}x^2-\frac{3}{2}) \\
x^2&=0 \ \vee \ \frac{1}{12}x^2-\frac{3}{2}=0
\end{align*}
Bei $0$ ist eine doppelte Nullstelle.
Beispielgraph zur Veranschaulichung
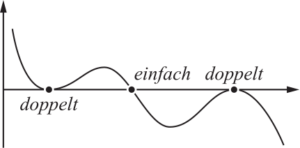
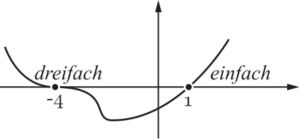
Dreifache Nullstelle
\begin{align*}
f(x)=(x+4)^3(x-1)
\end{align*}
Bei $-4$ ist somit eine dreifache Nullstelle.
Abschnittsweise definierte Funktionen
In der Mathematik ist eine abschnittsweise definierte Funktion eine Funktion, die mehrere Unter-Funktionen hat, und jede ist gültig für bestimmte Werte für $x$! Wir betrachten die Funktion
\begin{align*}
g(x)=\left\{ \begin{array}{ll} f(x) \ \ \text{für} \ \ 0 \leq x \leq 2 \\
h(x) \ \ \text{für} \ \ x>2 \end{array} \right.
\end{align*}
Das bedeutet, das für $x$-Werte zwischen $0$ und $2$ die Funktion $f(x)$ den Verlauf von $g(x)$ beschreibt. Für $x$-Werte größer $2$, wird die Funktion $g(x)$ durch $h(x)$ beschrieben.
Alles zum Thema Achsen findest du in diesem Video!
Abstand von zwei Punkten
Eine allgemeine Formel, die den Abstand von zwei Punkten berechnet, lautet
\begin{align*}
d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}
\end{align*}
Beispiel
Berechne den Abstand der Punkte $P_1(1|2); ~ Q(3|10)$
\begin{align*}
d&=\sqrt{(1-3)^2+(2-10)^2} \\
d&= 8,25 \ [\textrm{LE}]
\end{align*}
Senkrechter Abstand
Für den senkrechten Abstand zweier Funktionen bildet man die Differenzenfunktion
\begin{align*}
d(x)=g(x)-f(x).
\end{align*}
Den Abstand muss man häufig bei Extremwertaufgaben oder bei der Fläche zwischen 2 Graphen bestimmen.
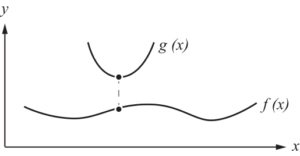
Dabei beschreibt $d(x)$ die Zielfunktion, die die Differenz der beiden Funktionen $f$ und $g$, also den senkrechten Abstand angibt. Diese Funktion muss auf Extremstellen untersucht werden. Wenn ein Hochpunkt rauskommt ist der senkrechte Abstand maximal und wenn ein Tiefpunkt rauskommt ist der senkrechte Abstand minimal.
Jetzt Lernvideo zum Thema Senkrechter Abstand von Daniel anschauen
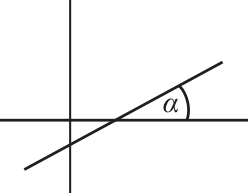
Winkel zwischen einer Geraden und x-Achse
Der Steigungswinkel einer Geraden ist derjenige im mathematisch positiven Sinn (gegen den Uhrzeigersinn) gemessene Winkel $\alpha$, den die Gerade mit der positiven $x$-Achse einschließt. Der Tangens des Steigungswinkels einer Geraden ist für $\alpha \neq 90$ gleich ihrer Steigung $m$: $\tan (\alpha)=m$
Erklärvideo zum Schnittwinkel mit der x-Achse
Erklärvideo zum Schnittwinkel mit der y-Achse
Winkel zwischen zwei Geraden
Der Schnittwinkel $\alpha$ zwischen den Graphen zweier linearer Funktionen mit den Steigungen $m_1$ bzw. $m_2$ berechnet sich mittels
\begin{align*}
\tan(\alpha) = \left|\frac{m_1 – m_2}{1+m_1m_2}\right|
\end{align*}
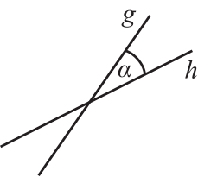
Stehen die Geraden senkrecht zueinander, gilt: $m_1 \cdot m_2=-1$
Achtung bei kurvigem Verlauf zweier Funktionen: dann erst Steigungen an gefragter Stelle bestimmen und diese dann multiplizieren!
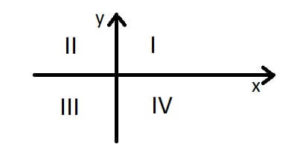
Quadranten
Die Abbildung zeigt, welchen Bereich des Koordinatensystems mit welchem Quadranten beziffert werden. So heißt z.B. der Bereich oberhalb der $x$-Achse und rechts der $y$-Achse Quadrant I.