
Stetigkeit
Eine Funktion ist stetig, wenn der Graph der Funktion im Definitionsbereich nahtlos gezeichnet werden kann. Anders ausgedrückt: Der Graph muss in jedem zusammenhängenden Teilintervall aus dem Definitionsbereich nahtlos gezeichnet werden können.
Allgemein ist Stetigkeit über das $\epsilon – \delta$-Kriterium definiert, mit dem wir uns am Ende dieser Seite noch beschäftigen werden. Für Funktionen in lediglich einer Veränderlichen (also das, was wir hier behandeln) reduziert sich der Stetigkeitsnachweis erheblich, und zwar auf die Berechnung von links- und rechtsseitigen Grenzwerten.
Eine gute Übersicht über das Thema Stetigkeit erhältst du in diesem Lernvideo:
Stetigkeitsnachweis in $x_0$
Für den Stetigskeitsnachweis müssen wir zeigen, dass die folgenden drei Werte, falls sie definiert sind, an der Stelle $x_0$ gleich sind:
- Funktionswert an der Stelle $x_0$
- Linksseitiger Grenzwert an der zu untersuchenden Stelle $x_0$
- Rechtsseitiger Grenzwert an der zu untersuchenden Stelle $x_0$
Mathematische Darstellung der Werte:
\begin{align*}
f(x_0)=\lim\limits_{x \uparrow x_0}{f(x)}=\lim\limits_{x \downarrow x_0}{f(x)}\qquad\text{oder nur}\qquad f(x_0)=\lim\limits_{x \rightarrow x_0}{f(x)}
\end{align*}
Der Funktionswert $f(x_0)$ ist immer definiert. Die beiden anderen Funktionswerte müssen nicht definiert sein (z.B. am Rand eines abgeschlossenen Intervalls des Definitionsbereichs).
Daniel erklärt das Ganze leicht verständlich in diesem Lernvideo!
Hierzu ein Beispiel:
${f}:{[0,\infty)}{\in\mathbb{R}}{\sqrt{x}},\ f$ ist in $x_0=0$ stetig.
Hier existiert kein linksseitiger Grenzwert, da 0 den Definitionsbereich $[0,\infty)$ linksseitig abschließt.
Daraus ergibt sich, dass Funktionen in isolierten Punkten automatisch stetig sind (auch über $\epsilon – \delta$-Kriterium einfach zu zeigen).
Rechenregeln
Für verschiedene stetige Funktionen ($f$ und $g$) gelten folgende Rechenregeln:
- $f+g, f-g$ sind stetig (Summe, Differenz)
- $f\cdot g$ ist stetig (Produkt)
- $\frac{f}{g}$ ist stetig (Quotient; nur wenn $g \neq 0$)
- $f(g(x)), g(f(x))$ sind stetig (Verknüpfungen/Verkettungen)
Stetig sind:
Alle Polynome, Potenz-, Exponential- und Logarithmusfunktionen sowie die trigonometrischen und hyperbolischen Funktionen. Dies sind elementare Funktionen. Stetigkeit auf ihren Definitionsbereichen ist bekannt und darf in Prüfungen so verwendet/vorausgesetzt werden.
Auch Funktionen mit Polstellen, also z.B. rationale Funktionen mit Nullstellen im Nenner (auch die Tangens-Funktion) sind stetig! Also gilt: immer auf den Definitionsbereich der Funktion achten (Polstellen sind nicht Teil der Funktion)!
Linksseitige und rechtsseitige Grenzwerte
Die Grenzwertuntersuchung an einer bestimmten Stelle $x_0$ von links und von rechts ergibt, nur Sinn bei einer Funktion mit lediglich einer Variable. Wir notieren ganz allgemein den Grenzwert gegen ein bestimmtes $x_0$ mit $\lim\limits_{x \rightarrow x_0}$ (Schreibweise, wenn links- und rechtsseitiger Grenzwert übereinstimmen).
Grenzwert gegen ein bestimmtes $x_0$
von links: $\lim\limits_{x \uparrow x_0}{f(x)}$
von rechts: $\lim\limits_{x \downarrow x_0}{f(x)}$
$x_0$ ist ein Häufungspunkt der betrachteten Menge und muss deshalb nicht im Definitionsbereich der Funktion liegen.
Der links- und rechtsseitigen Grenzwert wird dir hier im Lernvideo nochmals anschaulich dargestellt:
Beispiel 1:
${g:}{\in\mathbb{R}\setminus\{-1\}}\longrightarrow \mathbb{R} \frac{x+2}{x+1},\quad x_0=-1 $
$\lim\limits_{x \uparrow -1}\ {g(x)}=-\infty$ (Zähler positiv, Nenner nähert sich negativ der Null)
$\lim\limits_{x \downarrow -1}{g(x)}=\infty$ (Zähler positiv, Nenner nähert sich positiv der Null)
$\longrightarrow x = -1$ ist eine Polstelle mit Polwechsel von $-\infty$ nach $\infty$
$\longrightarrow g$ ist trotzdem auf seinem Definitionsbereich $\mathbb{R}\setminus\{-1\}$ stetig, da es aus stetigen Funktionen zusammengesetzt ist.
Beispiel 2:
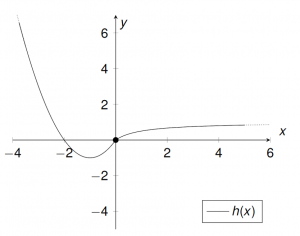
${h:}\mathbb{R}\longrightarrow\mathbb{R}=\quad{\begin{cases} (x+1)^2-1 \ \ & x<0\\ \frac{x}{x+1}\ \ & x\geq 0 \end{cases}} ,\quad x_0=0 \\$$\lim\limits_{x \uparrow 0}{h(x)}=\lim\limits_{x \uparrow 0}\ (x+1)^2-1=1^2-1=0 \\ $
$\lim\limits_{x \downarrow 0}{h(x)}=\lim\limits_{x \downarrow 0}\ x+1=0 \\ $
$h(0)=0 \\ $
$\longrightarrow h$ ist in $x=0$ stetig (auch auf ganz $\mathbb{R}$ stetig, da es aus stetigen Funktionen zusammengesetzt ist).
Beispiel 3:
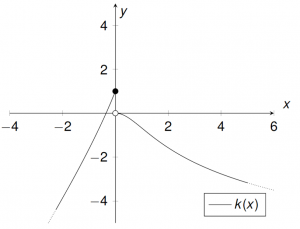
$k: \mathbb{R}\longrightarrow\mathbb{R}{\begin{cases} 2x+\text{e}^x & x\leq0 \\ x-\ln(x^2+1)& x>0\end{cases}},\quad x_0=0$
$\lim\limits_{x \uparrow 0}{k(x)}=\lim\limits_{x \uparrow 0}{2x+\text{e}^x}=0+\text{e}^0=1$
$\lim\limits_{x \downarrow 0}{k(x)}=\lim\limits_{x \downarrow 0}{x-\ln(x^2+1)}$
$\phantom{\lim\limits_{x \downarrow 0}{k(x)}}= 0-\ln(1)=0-0=0$
$\Rightarrow h$ ist nicht auf seinem ganzen Definitionsbereich $\mathbb{R}$ stetig (unstetig in $x=0$ (Sprungstelle); auf $\mathbb{R}\setminus\{0\}$ allerdings stetig, da es aus stetigen Funktionen zusammengesetzt ist).
Stetige Erweiterung
Wir gehen hier der Frage nach, ob sich die vorliegende Funktion an gewissen Stellen „reparieren“ lässt, damit die Funktion dort stetig wird. Umgangssprachlich lässt sich eine Funktion in einem (Häufungs)Punkt $x_0$ stetig erweitern, wenn sie dort eine Definitionslücke besitzt, die aber keine Polstelle oder „entnommene“ Sprungstelle ist. Folglich existiert für die Funktion anschaulich keine andere Möglichkeit, als von beiden Seiten in einem Punkt zu enden (Achtung, anschaulich aber schwammig!, $\ast^1$). $x_0$ wird dann auch (be)hebbare Definitionslücke genannt.
Eine Erklärung zur (be)hebbaren Definitonslücke kannst du dir in diesem Lernvideo anschauen:
Stetig erweiterbar in $x_0$
Links- und rechtsseitige Grenzwert an einer Stelle $x_0$ müssen existieren (also $\lim\limits_{x \uparrow 0}{f(x)}$ und $\lim\limits_{x \downarrow 0}{f(x)}$ müssen konvergieren) und übereinstimmen, $x_0$ liegt jedoch nicht im Definitionsbereich der eigentlichen Funktion.
Mathematisch ausgedrückt:
\begin{align*}
f(x_0)=\lim\limits_{x \uparrow x_0}{f(x)} = \lim\limits_{x \downarrow x_0}{f(x)} \neq \pm \infty
\end{align*}
Beispiel 1
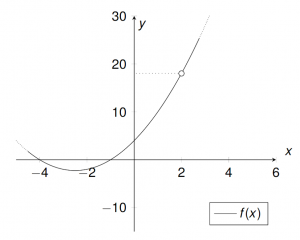
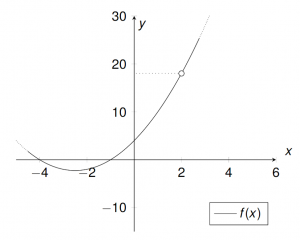
${f}{x}{\mathbb{R}\setminus\{2\}}{\mathbb{R}}{\frac{x^3+3x^2-6x-8}{x-2}},\quad x_0=2$$\stackrel{\text{per HS}}{\Rightarrow} f(x) = x^2+5x+4\ ,\quad x\neq 2$
$\phantom{\stackrel{\text{per HS}}{\Rightarrow}}\lim\limits_{x \uparrow 2}{f(x)}=4+10+4=18$
$\phantom{\stackrel{\text{per HS}}{\Rightarrow}}\lim\limits_{x \downarrow 2}{f(x)}=4+10+4=18$
Die Funktion $f$ lässt sich an der Stelle $x_0=2$ stetig erweitern:
$\Rightarrow \tilde{f}:\mathbb{R} \rightarrow \mathbb{R}, \tilde{f}(x){x^2+5x+4}=\begin{cases} \frac{x^3+3x^2-6x-8}{x-2} & x\neq 2 \\ 18 & x=2\end{cases}$
Beispiel 2
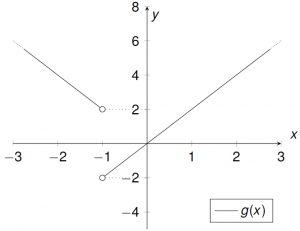
${g}:\mathbb{R}\setminus\{-1\}\longrightarrow{\mathbb{R}},\ \ g(x){\frac{2x|{x+1}|}{x+1}},\quad x_0=-1$$\lim\limits_{x \uparrow -1}{g(x)}=\lim\limits_{x \uparrow -1}{\frac{2x(-(x+1))}{x+1}}=\lim\limits_{x \uparrow -1}{-2x}=2$
$\lim\limits_{x \downarrow -1}{g(x)}=\lim\limits_{x \downarrow -1}{\frac{2x(x+1)}{x+1}}=\lim\limits_{x \downarrow -1}{2x}=-2$
Die Funktion $g$ lässt sich an der Stelle $x_0=-1$ nicht stetig erweitern (Sprungstelle).
Beispiel 3
Existieren Zahlen $t\in\mathbb{R}$, sodass die Funktion $h$ in $x=0$ stetig fortsetzbar wird? Falls ja, gib $t$ an und setze $h$ stetig fort.
\begin{align*}
&{h}:{\mathbb{R}\setminus\{1\}}{\mathbb{R}}{\begin{cases} -2t\exp^{\exp^{\frac{1}{x-1}}} & x<1 \\ -\left(\frac{x-t}{\sqrt{t}-\sqrt{x}}\right)^2& x>1\end{cases}}
\end{align*}
Linksseitig:
$\lim\limits_{x \uparrow 1}{h(x)}=\lim\limits_{x \uparrow 1}{-2t\exp^{\exp^{\frac{1}{x-1}}}}=-2t,\quad\text{da (hier mal ganz ausführlich):}$
$\lim\limits_{x \uparrow 1}{x-1}=0 \text{ (nähert sich negativ der 0), daraus folgt:}$
$\lim\limits_{x \uparrow 1}{\frac{1}{x-1}}=-\infty (\frac{1}{0}=\pm\infty \text{ da Nenner neg.: } -) \infty, \text{ daraus folgt: }$
$\lim\limits_{x \uparrow 1}{\exp^{\frac{1}{x-1}}}=0 \text{ („$\exp^{-\infty}=0$“), daraus folgt dann:}$
$\lim\limits_{x \uparrow 1}{\exp^{\exp^{\frac{1}{x-1}}}}=1 \text{ ($\exp^0=1$), daraus folgt dann der obenstehende Grenzwert.}$
Rechtsseitig:
$\lim\limits_{x \downarrow 1}{h(x)}=\lim\limits_{x \downarrow 1}{-\left(\frac{x-t}{\sqrt{t}-\sqrt{x}}\right)^2}=\lim\limits_{x \downarrow 1}{-\left(\frac{(\sqrt{x}-\sqrt{t})(\sqrt{x}+\sqrt{t})}{\sqrt{t}-\sqrt{x}}\right)^2}$
$\lim\limits_{x \downarrow 1}{-\left(-\frac{(-\sqrt{x}+\sqrt{t})(\sqrt{x}+\sqrt{t})}{\sqrt{t}-\sqrt{x}}\right)^2}=\lim\limits_{x \downarrow 1}{-\left(-(\sqrt{x}+\sqrt{t})\right)^2}\\
=\lim\limits_{x \downarrow 1}{-\left(\sqrt{x}+\sqrt{t}\right)^2}=-\left(1+\sqrt{t}\right)^2=-(1+2\sqrt{t}+t)=-1-2\sqrt{t}-t$
Grenzwerte gleichsetzen, um die $t$ auszurechnen, bei denen die Grenzwerte tatsächlich gleich sind:
$-1-2\sqrt{t}-t=-2t$
$\Leftrightarrow t-2\sqrt{t}-1=0\quad t \text{ substituieren, um quadratische Gleichung zu bekommen}$
$z:=\sqrt{t},\ z^2=t,\quad \Rightarrow z\geq 0\text{ (wegen der Wurzel)}$
$\Rightarrow z^2-2z-1=0$
$\Rightarrow z_{1,2}=1\pm\sqrt{1+1}=1\pm\sqrt{2} \ \stackrel{z\geq 0}{\Rightarrow} z=1+\sqrt{2}$
$\stackrel{t=z^2}{\Rightarrow} t =1+\sqrt{2}^2=1+2\sqrt{2}+2=3+2\sqrt{2}$
Für $t=3+2\sqrt{2}$ ist $h$ in $x=1$ stetig fortsetzbar. Nun das $t$ in einen der beiden Grenzwerte einsetzen, um den Funktionswert zu bestimmen, mit dem stetig fortgesetzt werden soll:
$\tilde h(1)=-2(3+2\sqrt{2})=-6-4\sqrt{2}$$\tilde{h}:\mathbb{R} \longrightarrow \mathbb{R}{\begin{cases} -2(3+2\sqrt{2})\exp^{\exp^{\frac{1}{x-1}}} & x<1 \\ -6-4\sqrt{2} & x=1 \\ -\left(\sqrt{x}+\sqrt{3+2\sqrt{2}}\right)^2& x>1\end{cases}}$
Epsilon-Delta-Kriterium für Stetigkeit
Wie schon erwähnt, ist das offizielle und mathematisch allgemeine Verfahren für einen Stetigkeitsnachweis in einem Punkt $x_0$ das $\epsilon – \delta$-Kriterium, das formal so aussieht:
\begin{align}
&\forall\epsilon>0\ \exists\delta>0\ \forall x\in\ D:\ {|x-x_0|}<\delta\ \Rightarrow\ {|f(x)-f(x_0)|}<\epsilon
\end{align}
Wenn wir uns diese Definition/dieses Kriterium ansehen, könnten wir meinen, hier wird sprichwörtlich mit Kanonen auf Spatzen geschossen oder im studentischen Fachjargon „Man kann es nicht komplizierter ausdrücken!“.
Wie ist das zu lesen und was ist zu tun? Es ähnelt im Aufbau dem $\epsilon$-Kriterium aus dem Thema Folgen; daher ist die Vorgehensweise/der strukturelle Ablauf sehr ähnlich, im Allgemeinen aber leider „stressiger“. In Worten ist:
„Für alle (vorgegebenen) Epsilons größer Null gibt es ein positives Delta, sodass für alle $x$ aus dem Definitionsbereich der Funktion die folgende Implikation gilt: Wenn der Abstand von $x$ zu $x_0$ kleiner Delta ist, dann ist auch der Abstand der zugehörigen Funktionswerte kleiner Epsilon.“
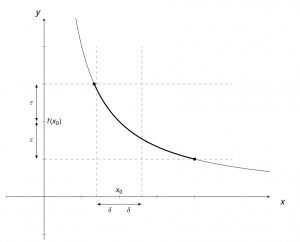
Deine Aufgabe ist, das $\delta$ in Abhängigkeit von (einem vorgegebenen) $\epsilon$ auszudrücken. Auch wenn kein fester Zahlenwert für $\epsilon$ in der Fragestellung angegeben ist, ist dies die vorgegebene Größe. Du bist am Ziel, wenn du am Ende eine „Funktionsvorschrift“ $\delta(\epsilon)$ gefunden hast, die immer erfüllt ist.
Wenn $\epsilon$ kleiner wird (gegen Null läuft), dann muss passend dazu auch $\delta$ kleiner werden (gegen Null laufen). Das „passend dazu“ drückst du mathematisch durch das $\delta(\epsilon)$ aus:
${|f(x)-f(x_0)|}=\ldots\leq\ldots\cdot {|x-x_0|}<\underbrace{\ldots\cdot\delta<\epsilon}_{\ast^1} \qquad \ast^1\ \Rightarrow\ \delta(\epsilon)=\ldots$Oft ist bei der Abschätzung die von Mathematikern geliebte Dreiecksungleichung zu benutzen, denn du darfst in dem Ausdruck am Ende nur $\delta$, $\epsilon$ und Zahlen aus $\mathbb{R}$ stehen haben. Sind noch weitere $x$ im Term enthalten, müssen diese geschickt umgeschrieben/nach oben abgeschätzt werden (Dreiecksungleichung), zu Ausdrücken $|{x-x_0}|$, die dann wieder durch $\delta$ ersetzt werden können.
${f}:{\mathbb{R}}{(0,1]}{\frac{1}{x^2+1}},\quad$ Zeige mit dem $\epsilon – \delta$-Kriterium: $f$ ist in $x_0=2$ stetig. Sei $\epsilon>0$, dann existiert zu jedem $\epsilon$ ein $\delta := -2+\sqrt{4+\epsilon}$, sodass:
\begin{align*}
|f(x)-f(x_0)|&=|\frac{1}{x^2+1}-\frac{1}{5}|=|\frac{5-(x^2+1)}{5(x^2+1)}|=|\frac{-x^2+4}{5(x^2+1)}|<|-x^2+4|\\ \\
&=|x^2-4|=|(x+2)(x-2)|<|(x+2)\cdot\delta| = |(x-2+4)|\cdot\delta\\ \\
&\leq \left(|x-2|+|4|\right)\cdot\delta < \left(\delta+4\right)\cdot\delta=\epsilon
\end{align*}
mit $\left(\delta+4\right)\cdot\delta=\epsilon \Leftrightarrow \delta^2+4\delta-\epsilon=0\ \Rightarrow\ \delta_{1,2}=-2\pm\sqrt{4+\epsilon}$, da $\delta>0$ folgt:
$\delta=-2+\sqrt{4+\epsilon}$