
Trassierung
Trassierungsaufgaben verlangen von uns, Funktionsgraphen, gerne auch zwei Geraden, knickfrei (glatter Übergang) zu verbinden.
Aus der Information knickfrei ziehen wir, dass die Steigung der Funktionen an den Punkten $P_1$ und $P_2$ gleich ist.
Weitere Begriffe, die im Zusammenhang mit Trassierung fallen, sind ohne krümmungsruck oder krümmungsruckfrei. Das bedeutet lediglich, dass die Krümmung am Übergangspunkt identisch sein soll. Für das nachfolgende Vorgehen soll $f$ die gesuchte Funktion sein, die die bekannten Funktionen $g$ und $h$ miteinander verbinden soll.
Vorgehen:
Schritt 1
Aufgabenstellung sorgfältig lesen – Welchen Grad soll die zu erstellende Funktion haben? Wenn im Text nicht anders vorgegeben, z.B. Funktion 2. Grades hat die Form
\begin{align*}
f(x)=ax^2+bx+c
\end{align*}
dann gilt meist:
- Treten nur die Begriffe ohne Sprung und ohne Knick / knickfrei auf hat die gesuchte Funktion den Grad 3.
\begin{align*}
f(x)=ax^3+bx^2+cx+d
\end{align*}
- Tritt zusätzlich der Begriff ohne krümmungsruck auf hat die gesuchte Funktion den Grad 5.
\begin{align*}
f(x)=ax^5+bx^4+cx^3+dx^2+ex+f
\end{align*}
Neu!
Schritt 2
Aufstellen der allgemeinen Funktionsgleichung $f(x)$ sowie der 1. und, wenn krümmungsruckfrei verlangt wird, 2. Ableitung
Schritt 3
Bedingungen aufstellen
- ohne Sprung: $g(x_1)=f(x_1)$ und $h(x_2)=f(x_2)$
- ohne Knick: $g'(x_1)=f'(x_1)$ und $h'(x_2)=f'(x_2)$
- ohne Krümmungsruck: $g“(x_1)=f“(x_1)$ und $h“(x_2)=f“(x_2)$
Schritt 4
Alle Informationen in mathematische Gleichungen übersetzen, LGS aufstellen und lösen.
Schritt 5
Funktionsgleichung aufschreiben
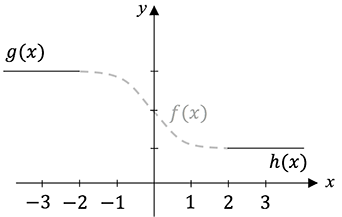
Beispiel Trassierung mit Geraden
Schauen wir uns dazu ein Beispiel an, um das Prinzip zu verstehen. Gegeben seien die Geraden auf ihren jeweils vorgegeben Definitionsbereichen
\begin{align*}
g(x)=3, \quad D_g=[-5;-2] \quad \textrm{und} \quad h(x)=1, \quad D_h=[2;4].
\end{align*}
In dieser Aufgabe soll die knickfreie Verbindung durch eine Funktion 3. Grades realisiert werden. Wie das ganze am Ende aussehen soll, zeigt die untere Abbildung. Wir arbeiten das obige Vorgehen ab und erkennen aus der Aufgabenstellung, dass die Funktion den Grad 3 haben soll. Eine ganz allgemeine Funktion dritten Grades sieht so aus: $f(x)=ax^3+bx^2+cx+d$
Es gilt also 4 Unbekannte zu bestimmen: $a$, $b$, $c$ und $d$. Dazu benötigen wir 4 Bedingungen. Zunächst aber bilden wir kurz die 1. Ableitung.
\begin{align*}
f'(x)=3ax^2+2bx+c
\end{align*}
Die 2. Ableitung ist nicht notwendig, da keine Information bezüglich des Krümmungsrucks vorliegt. Jetzt stellen wir die Bedingungen auf:
\begin{align*}
&\text{ohne Sprung:} &\quad g(-2) =f(-2) \quad &\Rightarrow &3=a(-2)^3+b(-2)^2-2c+d \\
&\text{ohne Sprung:} &\quad h(2) =f(2) \quad &\Rightarrow &1=a(2)^3+b(2)^2+2c+d \\
&\text{ohne Knick:} &\quad g'(-2) =f'(-2) \quad &\Rightarrow &0=3a(-2)^2+2\cdot(-2)b+c \\
&\text{ohne Knick:} &\quad h'(2) =f'(2) \quad &\Rightarrow &0=3a(2)^2+2 \cdot 2 b +c \\
\end{align*}
In diesem einfachen Beispiel ist die 1. Ableitung (Steigung) der Geraden $g$ und $h$ gleich Null, da die Geraden parallel zur $x$-Achse verlaufen. Das Gleichungssystem bestehend aus 4 Gleichungen müssen wir jetzt mit den uns bekannten Verfahren oder dem Taschenrechner lösen. In diesem Fall gibt es keine eindeutige Lösung, sondern unendlich viele. Wir sagen also, dass z.B. $a=1/16$ sei und daraus folgt für die anderen Koeffizienten: $b=0$, $c=-3/4$ und $d=2$. Die gesuchte Funktionsgleichung lautet
\begin{align*}
f(x)=\frac{1}{16}x^3-\frac{3}{4}x+2, \quad D_f=[-2;2].
\end{align*}
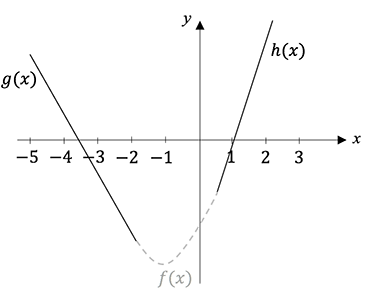
An dieser Stelle wollen wir uns noch ein weiteres Beispiel angucken, bei dem es eine eindeutige Lösung gibt. Es sind zwei Geraden
\begin{align*}
g(x)=-4x-14, \ \ -5 \leq x \leq -2 \quad \textrm{und} \quad h(x)=6x-6,5, \ \ 0,5 \leq x \leq 3,
\end{align*}
gegeben, die jeweils nur in einem bestimmten Abschnitt definiert sind. Diese beiden Geraden sollen nun so miteinander verbunden werden, dass sie eine knickfreie Parabel darstellen.
Die untere Skizze stellt die qualtiativen Verläufe der Geraden und der gesuchten Parabel anschaulich dar. Eine allgemeine Funktionsgleichung einer Parabel und dessen erster Ableitung lautet:
\begin{align*}
f(x)&=ax^2+bx+c \\
f'(x)&=2ax+b
\end{align*}
Es müssen 3 Unbekannte bestimmt werden. Im nächsten Schritt überlegen wir uns die Bedingungen.
\begin{align*}
\text{ohne Sprung:} \quad g(-2) &=f(-2) \quad \Rightarrow -6=a(-2)^2-2b+c \\
\text{ohne Sprung:} \quad h(0,5) &=f(0,5) \quad \Rightarrow -3,5=a(0,5)^2+0,5b+c \\
\text{ohne Knick:} \quad g'(-2) &=f'(-2) \quad \Rightarrow -4=-4a+b \\
\text{ohne Knick:} \quad h'(0,5) &=f'(0,5) \quad \Rightarrow 6=a+b \\
\end{align*}
Nach dem Auflösen des Gleichungssystem erhalten wir für die Unbekannten $a=2$,
$b=4$ und $c=-6$ und die gesuchte Parabelgleichung
\begin{align*}
f(x)=2x^2+4x-6, \quad D_f=[-2;0,5].
\end{align*}
Ausführliches Beispiel
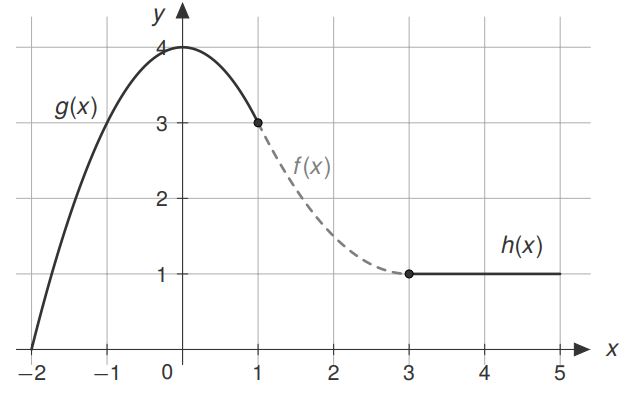
Gegeben seien die folgenden Funktionen auf ihren jeweils vorgegeben Definitionsbereichen:
\begin{align*}
g(x)=-x^2+4, \quad D_g=[-2;1] \quad \text{und} \quad h(x)=1, \quad D_h=[3;5].
\end{align*}
Die beiden gegebenen Funktionen sollen sprung- und knickfrei miteinander verbunden werden. Wie das ganze am Ende aussehen soll, zeigt die nebenstehende Abbildung. Wir arbeiten das obige Vorgehen ab und vermuten aus der Aufgabenstellung, dass die Funktion den Grad 3 haben soll. Eine ganz allgemeine Funktion dritten Grades sieht so aus: $f(x)=ax^3+bx^2+cx+d$.
Es gilt also 4 Unbekannte zu bestimmen: $a, b, c$ und $d$.
\begin{array}{rllcrcrcrcrcr}
I & sprungfrei: &g(1)=f(1) & \Rightarrow & 3 & = & a &+&b&+&c&+ &d \\
II & sprungfrei: &h(3)=f(3) & \Rightarrow & 1 & = & 27a&+&9b&+&3c&+ &d \\
III & knickfrei: &g'(1)=f'(1) & \Rightarrow & -2 & = & 3a&+&2b&+&c& &\\
IV & knickfrei: &h'(3)=f'(3) & \Rightarrow & 0 & = & 27a&+&6b&+&c& &
\end{array}
Das Gleichungssystem, bestehend aus 4 Gleichungen, müssen wir jetzt mit den uns bekannten Verfahren oder dem Taschenrechner lösen. Für die gesuchten Parameter erhalten wir $a=0$, $b=1/2$, $c=-3$ und $d=11/2$.
Die gesuchte Funktionsgleichung lautet demnach:
\begin{align*}
f(x)=\frac{1}{2} x^2-3x+ \frac{11}{2}, \quad D_f=[1;3].
\end{align*}
An dieser Stelle erweitern wir das obige Beispiel und nehmen an, dass die gesuchte Funktion zusätzlich krümmungsruckfrei sein soll. Die ersten 4 Bedingung können aus dem obigen Beispiel übernommen werden, allerdings ist die gesuchte Funktion nun 5. Grades:
\begin{align*}
f(x)&=ax^5+bx^4+cx^3+dx^2+ex+f, \\ \quad f'(x)&=5ax^4+4bx^3+3cx^2+2dx+e, \quad f“(x)=20ax^3+12bx^2+6cx+2d
\end{align*}
Aufstellen der Bedingungen liefert das folgende LGS:
\begin{array}{rllcrcl}
I & sprungfrei: &g(1)=f(1) & \Rightarrow & 3 & = & a+b+c+d+e+f \\
II & sprungfrei: &h(3)=f(3) & \Rightarrow & 1 & = & 243a+81b+27c+9d+3e+f \\
III & knickfrei: &g'(1)=f'(1) & \Rightarrow & -2 & = & 5a+4b+3c+2d+e \\
IV & knickfrei: &h'(3)=f'(3) & \Rightarrow & 0 & = & 405a+108b+27c+6d+e \\
V & krümmungsruckfrei: &g“(1)=f“(1) & \Rightarrow & -2 & = & 20a+12b+6c+2d \\
VI & krümmungsruckfrei: &h“(3)=f“(3) & \Rightarrow & 0 & = & 540a+108b+18c+2d
\end{array}
Lösen des LGS liefert die gesuchte Funktion $f(x)=\frac{1}{8}x^5-\frac{3}{2}x^4+\frac{27}{4}x^3-\frac{27}{2}x^2+\frac{81}{8}x+1$.
Neu!

