
Trigonometrische Funktionen
Themen auf dieser Seite
Sinusfunktion
Wichtige Eigenschaften der Sinusfunktion $f(x)=\sin(x)$:
- Die Sinusfunktion ist eine periodische Funktion mit Periode $2\pi$, d.h. dass der Graph der Sinusfunktion sich nach jeder Periode wiederholt.
- Definitionsbereich $D=\mathbb{R}$
- $W=[-1;1]$
- schneidet die $y$-Achse bei (0|0)
- punktsymmetrisch zum Ursprung
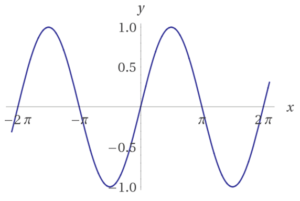
Die allgemeine Sinusfunktion lautet: $f(x)=a \sin(bx+c) +d$
Neu!
Cosinusfunktion
Wichtige Eigenschaften der Cosinusfunktion $f(x)=\cos(x)$:
- Die Cosinusfunktion ist eine periodische Funktion mit Periode $2\pi$, d.h. dass der Graph der Cosinusfunktion sich nach jeder Periode wiederholt.
- Definitionsbereich $D=\mathbb{R}$
- $W=[-1;1]$
- schneidet die $y$-Achse bei (0|1)
- achsensymmetrisch zum Ursprung
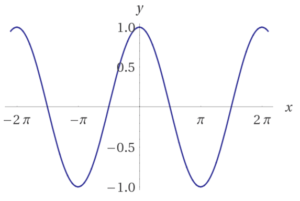
Die allgemeine Cosinusfunktion lautet: $f(x)=a \cos(bx+c) +d$
Tangensfunktion
Wichtige Eigenschaften der Tangensfunktion $f(x)=\tan(x)$:
- die Tangensfunktion sich in regelmäßigen Abständen wiederholt, deswegen nennt man die Tangensfunktion auch periodisch
- Den Abstand zwischen zwei Wiederholungen nennt man die kleinste Periode $T$.
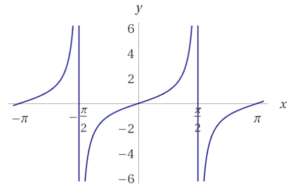
- Eine weitere Eigenschaft der Tangensfunktion ist, dass ihr Graph punktsymmetrisch zum Ursprung $(0/0)$ ist
- $W=\mathbb{R}$
Ableiten von sin, cos und tan
Schau dir zur Einführung das Lernvideo zum Thema Ableiten der Trgonometrischen Funktionen an.
Übersicht über Ableitungen der Sinus- und Cosinusfunktion:
\begin{align*}
f(x) = \sin(x) \quad &\Rightarrow \quad f'(x) = \cos(x) \\
f(x) = \cos(x) \quad &\Rightarrow \quad f'(x) = -\sin(x) \\
f(x) = -\sin(x) \quad &\Rightarrow \quad f'(x) = -\cos(x) \\
f(x) = -\cos(x) \quad &\Rightarrow \quad f'(x) = \sin(x)
\end{align*}
Die Ableitung des Tangens ist ein wenig schwieriger:
\begin{align*}
f(x)=\tan(x)= \quad \Rightarrow \quad f'(x) = \frac{1}{\cos^2(x)} = 1 + \tan^2(x)
\end{align*}
Der Tangens kann auch mit der Quotientenregel abgeleitet werden, wenn man weiß, dass der Tangens mit Sinus und Cosinus zu
\begin{align*}
f(x)=\tan(x)=\frac{\sin(x)}{\cos(x)}
\end{align*}
umgeschrieben werden kann. Dann folgt für die Ableitung
\begin{align*}
f'(x)=\frac{\cos^2(x)+\sin^2(x)}{\cos^2(x)} =\frac{1}{\cos^2(x) }
\end{align*}
mit $\cos^2(x)+\sin^2(x)=1$.
Schau dir zur Vertiefung Daniels Playlist zum Thema Trigonometrische Funktionen an.

