
Vektoren
Das Thema Vektoren begleitet dich nicht nur während deiner Schullaufbahn, sondern ist auch relevant für dein Studium oder deine Ausbildung. Wir haben für dich in diesem Artikel alle relevanten Themen zu Vektoren aufgelistet und in leicht verständlicher Sprache erklärt. Zusätzlich findest du passende Erklärvideos von Daniel Jung, damit du dein Wissen vertiefen kannst.
Inhaltsverzeichnis
- Grundlagen zu Vektoren
- Vom Punkt zum Vektor
- Unterschied Ortsvektor/Richtungsvektor
- Länge eines Vektors
- Rechnen mit Vektoren
- Mittelpunkt einer Strecke
- Lineare Abhängigkeit und Unabhängigkeit von Vektoren
- Koordinatenebenen
Neu!
Grundlagen zu Vektoren
Zu einem beliebigen Punkt im dreidimensionalem Raum ($x_1|x_2|x_3$) bzw. ($x|y|z$), z.B. $P( 6 | 7 | 4 )$, gelangt man, indem man vom Nullpunkt des Koordinatensystems 6 Einheiten in $x$-Richtung, 7 Einheiten in $y$-Richtung und dann 4 Einheiten in $z$-Richtung geht. Hier noch besondere Punkte.
In 2D gilt: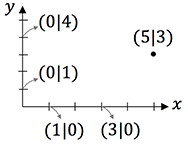
- Alle Punkte auf der $y$-Achse haben den $x$-Wert 0! $P_y(0|y)$
- Alle Punkte auf der $x$-Achse haben den $y$-Wert 0! $P_x(x|0)$
In 3D gilt: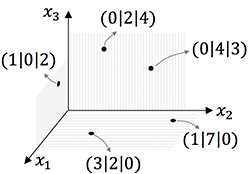
- Alle Punkte in der $x_1x_2$-Ebene haben den $x_3$-Wert 0! $P(x_1|x_2|0)$
- Alle Punkte in der $x_2x_3$-Ebene haben den $x_1$-Wert 0! $P(0|x_2|x_3)$
- Alle Punkte in der $x_1x_3$-Ebene haben den $x_2$-Wert 0! $P(x_1|0|x_3)$
Daniel erklärt euch nochmals in seinem Lernvideo, wie man Punkte abliest.
Vom Punkt zum Vektor
Ein Vektor beschreibt eine Parallelverschiebung in der Ebene oder im Raum. Aus zwei Punkten im 3-dimensionalem Raum $A(a_1|a_2|a_3)$ und $B(b_1|b_2|b_3)$ erhält man den Vektor
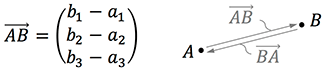
Grafisch wird der Vektor durch einen Pfeil dargestellt, der vom Punkt $A$ zum Punkt $B$ zeigt. Ein Vektor gibt somit die Verschiebung eines Punktes an!
Daniel erklärt euch nochmal, wie du vom Punkt zum Vektor kommst!
Unterschied Ortsvektor/Richtungsvektor
Ist $O(0|0)$ der Koordinatenursprung und $P(5|2)$ ein Punkt, so heißt der Vektor $\overrightarrow{OP} = \vec{p} = \left( \begin {array} {c}5-0\\2-0 \\\end {array} \right) = \left( \begin {array} {c}5 \\2 \\\end {array} \right)$ Ortsvektor zum Punkt $P$.
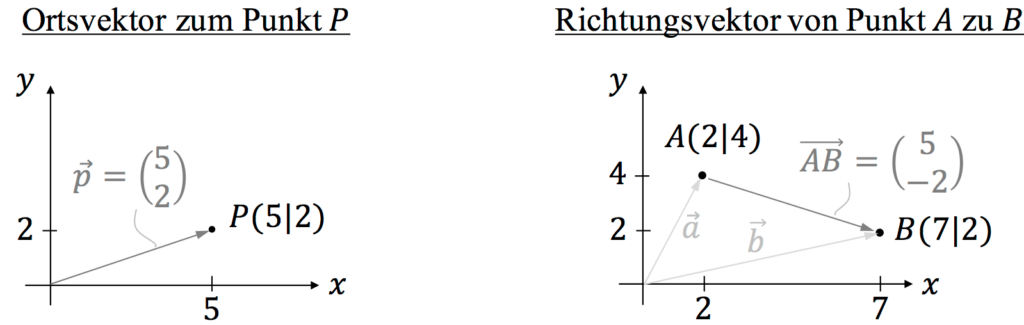
Richtungsvektoren können jeden Punkt als Startpunkt haben, während Ortsvektoren immer vom Koordinatenursprung ausgehen. Zum Beispiel lautet der Richtungsvektor zwischen $A(2|4)$ und $B (7|2)$:
\begin{align*}g
\overrightarrow{AB} = \vec{b} – \vec{a} = \left( \begin{array}{c} 7-2 \\ 2 – 4 \end{array} \right) = \left( \begin{array}{c} 5 \\ -2 \end{array} \right). \notag
\end{align*}
Zwei Richtungsvektoren sind identisch, wenn sie gleich lang sind und die gleiche Richtung haben. Im dreidimensionalem Raum werden Orts- und Richtungsvektoren genau wie im zwei-dimensionalen aufgestellt. Einziger Unterschied ist die zusätzliche Koordinate $x_3$ (oder $z$).
Schau dir zur Vertiefung nochmal das Lernvideo zum Thema Richtungs- und Ortsvektor an.
Länge eines Vektors
In kartesischen Koordinaten kann die Länge von Vektoren nach dem Satz des Pythagoras berechnet werden. Gegeben sei Vektor $A= (2 , 1 , 4)^T$ – Hinweis: Schreibweise mit „hoch $T$“ (Transponierte einer Matrix) ist oft platzsparender! Bitte nicht verzweifeln, es gilt:
\begin{align*}
A= (2 , 1 , 4)^T = \left( \begin{array}{c} 2 \\ 1 \\ 4 \end{array} \right), \notag
\end{align*}
dann wird die Länge über $|A|= \sqrt{2^2 + 1^2+ 4^2}$ bestimmt. Oder allgemein mit
\begin{align*}
a = |\vec{a}| = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}. \notag
\end{align*}
Alternativ kann die Länge auch als die Wurzel des Skalarprodukts angeben werden:
\begin{align*}
a = |\vec{a}| = \sqrt{\vec{a}\bullet \vec{a}}. \notag
\end{align*}
Vektoren der Länge 1 heißen Einheitsvektoren oder normierte Vektoren. Hat ein Vektor die Länge 0, so handelt es sich um den Nullvektor.
Lass dir von Daniel erklären, wie man die Länge eines Vektors bestimmt.
Rechnen mit Vektoren
- Addieren/Subtrahieren – Rechenregel gilt für $+$ und $–$, kurz: $\pm$
\begin{align*}\vec{a} \pm \vec{b} =\left( \begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array} \right) \pm\left( \begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array} \right) &=\left( \begin{array}{c} a_1 \pm b_1 \\ a_2 \pm b_2 \\ a_3 \pm b_3 \end{array} \right) \notag \\ \notag \\\textrm{z.B.} \quad\left( \begin{array}{c} 2 \\ -1 \\ 5 \end{array} \right) +\left( \begin{array}{c} 8 \\ 1 \\ -3 \end{array} \right) &=\left( \begin{array}{c} 2+8\\ -1+1 \\ 5+(-3) \end{array} \right) =\left( \begin{array}{c} 10\\ 0 \\ 2 \end{array} \right) \notag\end{align*}
Grafisch kann man sich das wiefolgt veranschaulichen. Merkt euch: Es spielt keine Rolle, ob ihr $\vec{a}+\vec{b}$ oder $\vec{b}+\vec{a}$ rechnet. Es kommt immer das gleiche raus!
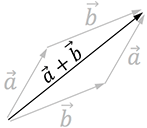
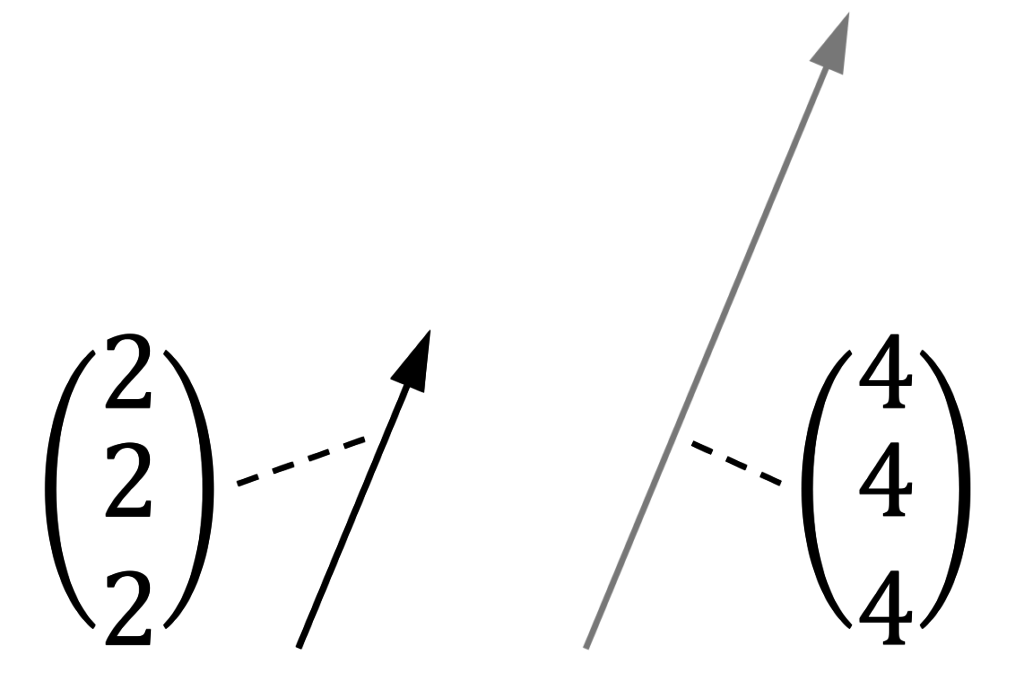
- Mit Zahl (Skalar) multiplizieren – Länge des Vektors ändert sich! Richtung bleibt gleich. \begin{align*}
2 \cdot \left( \begin{array}{c} 2 \\ 2 \\ 2 \end {array} \right) =
\left( \begin{array}{c} 2 \cdot 2 \\ 2 \cdot 2 \\ 2 \cdot 2 \end {array} \right) =
\left( \begin{array}{c} 4 \\ 4 \\ 4 \end {array} \right) \notag
\end{align*}
- Skalarprodukt:
Das Skalarprodukt (auch inneres Produkt, selten Punktprodukt) ist eine mathematische Verknüpfung, die zwei Vektoren eine Zahl (Skalar) zuordnet. Achtet auf die Unterscheidung des Malzeichens „$\cdot$“ und des Skalarproduktes „$\bullet$„.
Zudem ist es für die Berechnung von Winkeln zwischen Vektoren sinnvoll. Als allgemeines Rechenbeispiel folgt:
\begin{align*}
\vec a \bullet \vec b = a_1 \, b_1 + a_2 \, b_2 + a_3 \, b_3. \notag
\end{align*} Jetzt mal als Zahlenbeispiel:
\begin{align*}
\left( \begin {array}{c} 2 \\ 1 \\ 3 \end{array} \right)
&\bullet
\left( \begin{array}{c} 1 \\ 4 \\ 1 \end{array} \right) = 2 \cdot 1 + 1 \cdot 4 + 3 \cdot 1 = 9 \notag \\
\left( \begin {array}{c} 2 \\ 0 \\ 1 \end{array} \right)
&\bullet
\left( \begin{array}{c} -1 \\ 2 \\ 2 \end{array} \right) = -2+0+2 = 0 \notag
\end{align*}Achtung: Wenn $0$ raus kommt, dann sind die beiden Vektoren orthogonal/senkrecht zueinander!
Wofür wir das Skalarprodukt eigentlich brauchen:
- Winkelberechnung in der Ebene:
\begin{align*}
\cos(\alpha) = \frac{\vec{a} \ \bullet \ \vec{b}}{|\vec{a}| \cdot |\vec{b}|} =
\frac{a_1\ \cdot \ b_1 \ + \ a_2 \ \cdot \ b_2}{\sqrt{a_1^2+a_2^2}\ \cdot \ \sqrt{b_1^2 +\ b_2^2}}[/latex]
\end{align*}
- Winkelberechnung im Raum:
\begin{align*}
\cos(\alpha) = \frac{\vec{a} \ \bullet \ \vec{b}}{|\vec{a}|\ \cdot \ |\vec{b}|} = \frac{a_1\ \cdot \ b_1 \ + \ a_2 \ \cdot \ b_2 \ + \ a_3 \ \cdot \ b_3}{\sqrt{a_1^2 \ + \ a_2^2 \ + \ a_3^2}\ \cdot \ \sqrt{b_1^2 \ + \ b_2^2 \ + \ b_3^2}}[/latex]
\end{align*}
- Orthogonalität:
Wenn $\vec{a}$ und $\vec{b}$ orthogonal sind, dann gilt: $\vec{a} \bullet \vec{b} = 0$.
- Ermittlung eines Normalenvektors:
Bedingungen für einen Normalenvektor $\vec{n}$ von $\vec{a}$ und $\vec{b}$ sind:
$\vec{n} \bullet \vec{a} = 0$ und $\vec{n} \bullet \vec{b} = 0$
- Kreuzprodukt/Vektorprodukt:
Das Kreuzprodukt der Vektoren $1$ und $2$ ist ein Vektor, der senkrecht auf der von den beiden Vektoren aufgespannten Ebene steht und mit ihnen ein Rechtssystem bildet. Zahlenbeispiel: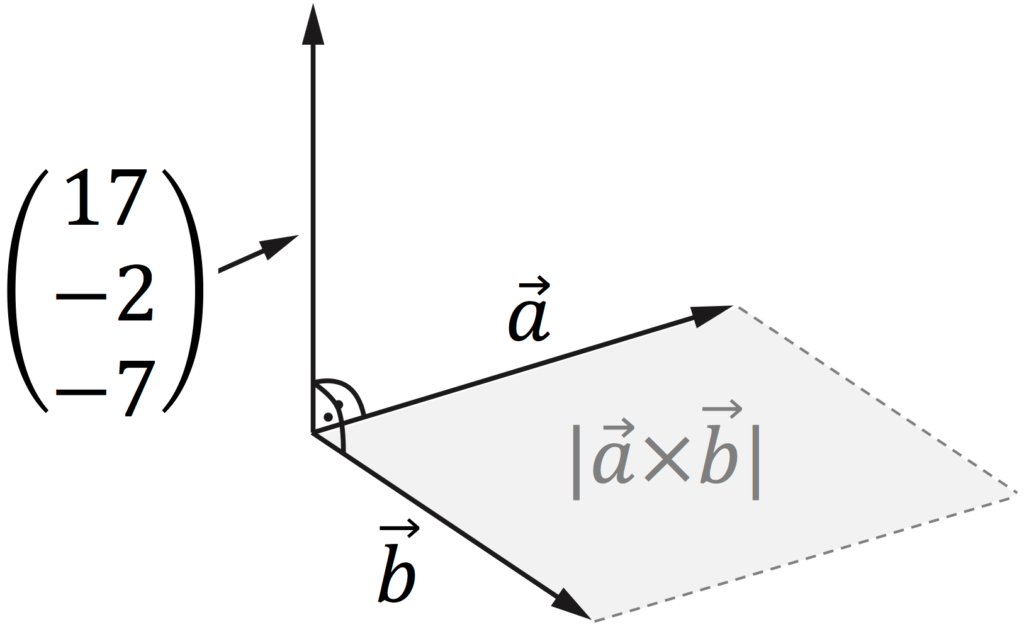
\begin{align*}
\left( \begin {array}{c} 2 \\ 3 \\ 4 \end{array} \right)
\times
\left( \begin{array}{c} 1 \\ -2 \\ 3 \end{array} \right)
=
\left( \begin {array}{c} 3 \cdot 3 – 4 \cdot (-2) \\ 4 \cdot 1 – 2 \cdot 3 \\ 2 \cdot (-2) – 3 \cdot 1 \end{array} \right) =
\left( \begin {array}{c} 17 \\ -2 \\ -7 \end{array} \right) \notag
\end{align*}
Wichtig: Die Länge dieses Vektors entspricht dem Flächeninhalt des Parallelogramms, das von den Vektoren $1$ und $2$ aufgespannt wird. Um zu überprüfen, ob wir richtig gerechnet haben, müsste das Skalarprodukt vom Vektor des Kreuzproduktes mit den zwei einzelnen Vektoren 0 ergeben:
\begin{align*}
\left( \begin {array}{c} 17 \\ -2 \\ -7 \end{array} \right)
\bullet
\left( \begin {array}{c} 2 \\ 3 \\ 4 \end{array} \right) = 34-6-28=0 \quad \notag \\
\left( \begin {array}{c} 17 \\ -2 \\ -7 \end{array} \right)
\bullet
\left( \begin {array}{c} 1 \\ -2 \\ 3 \end{array} \right) = 17+4-21=0 \quad \notag
\end{align*}
Es besteht damit die Möglichkeit, das Kreuzprodukt als Berechnung des $\vec{n}$-Vektors einer Ebene zu benutzen.
Allgemein gilt:
\begin{align*}
\vec{a}\times\vec{b} = \begin{pmatrix}a_1 \\ a_2 \\ a_3\end{pmatrix} \times \begin{pmatrix}b_1 \\ b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix} a_2b_3 – a_3b_2 \\ a_3b_1 – a_1b_3 \\ a_1b_2 – a_2b_1 \end{pmatrix}\,. \notag
\end{align*}Weiterer Hinweis: Die Kombination von Kreuz- und Skalarprodukt in der Form
\begin{align*}
(\vec{a} \times \vec{b}) \bullet \vec{c} \notag
\end{align*}
wird als Spatprodukt bezeichnet. Das Ergebnis ist eine Zahl, die dem orientierten Volumen des durch die drei Vektoren aufgespannten Spats entspricht.
Neu!
Anwendung
- Normalenvektor finden bei der Umwandlung von Ebenengleichungen in der Parameterform in die Koordinaten- oder Normalenform.
- Abstandsformel windschiefer Geraden.
- Flächeninhaltsberechnung von zwischen Vektoren aufgespannten Flächen.
Schau dir zur Vertiefung das Lernvideo zum Thema Rechnen mit Vektoren an!
Mittelpunkt einer Strecke
Gegeben sei die Strecke, die durch die Punkte $A$ und $B$ begrenzt wird. Gesucht sind die Koordinaten des Punktes $M$, der genau in der Mitte zwischen $A$ und $B$ liegt. Um diesen zu berechnen, muss man sich einer einfachen Formel bedienen:
\begin{align*}
&(2D) \ \ \ M \left( \frac{a_1 + b_1 }{2}\ | \ \frac{a_2 + b_2 }{2} \right) \notag \\
&(3D) \ \ \ M \left( \frac{a_1 + b_1 }{2}\ | \ \frac{a_2 + b_2 }{2}\ | \ \frac{a_3 + b_3 }{2} \ \right) \notag
\end{align*}
Beispiel: Berechne den Mittelpunkt der Punkte $A = (2|4|3)$ und $B=(10|16|5)$.
\begin{align*}
M_{AB} = \left( \frac{2 + 10 }{2} \ | \ \frac{4 + 16 }{2} \ | \ \frac{3 + 5 }{2} \right) = (6 | 10 | 4) \notag
\end{align*}
Einschub – Formel Schwerpunkt Dreieck: $ \overrightarrow{0S} = \frac{1}{3}( \overrightarrow{0A} + \overrightarrow{0B} + \overrightarrow{0C})$
Lass dir erklären, wie man den Mittelpunkt einer Strecke berechnet.
Lineare Abhängigkeit und Unabhängigkeit von Vektoren
Bevor wir uns angucken, wie man lineare Abhängkeit bzw. Unabhängigkeit nachweist, soll uns die folgende Abbildung zunächst einen Überblick geben, was für Fälle auftreten können. Wichtige Begriffe hierbei: Kollinear und Komplanar.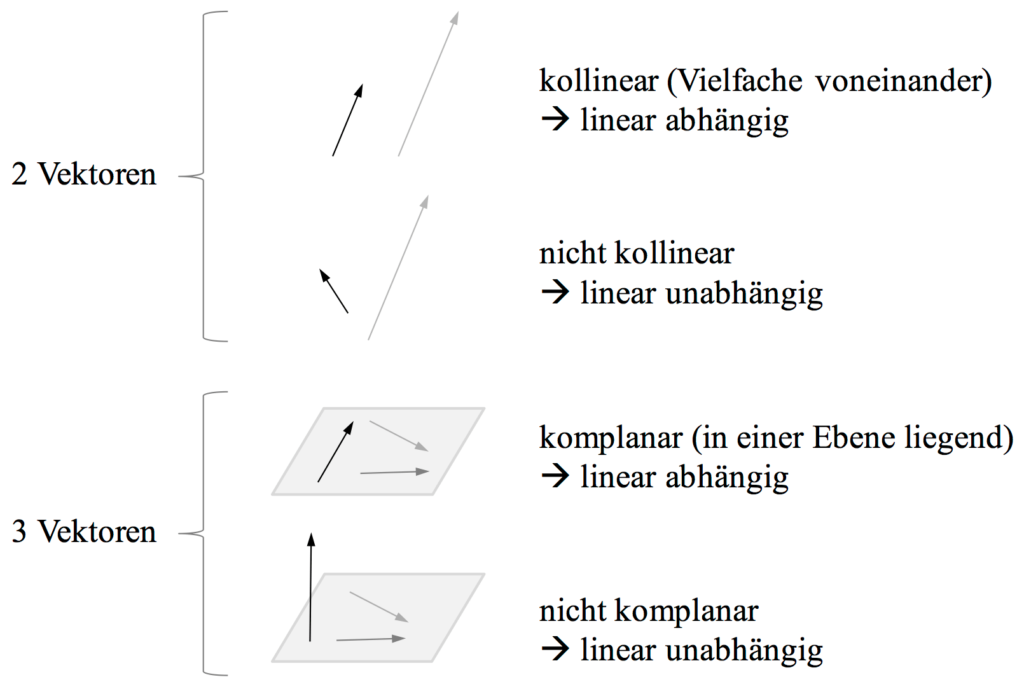
Wenn wir also nachweisen, dass zwei Vektoren kollinear bzw. drei Vektoren komplanar sind, wissen wir, dass die Vektoren linear abhängig sind.
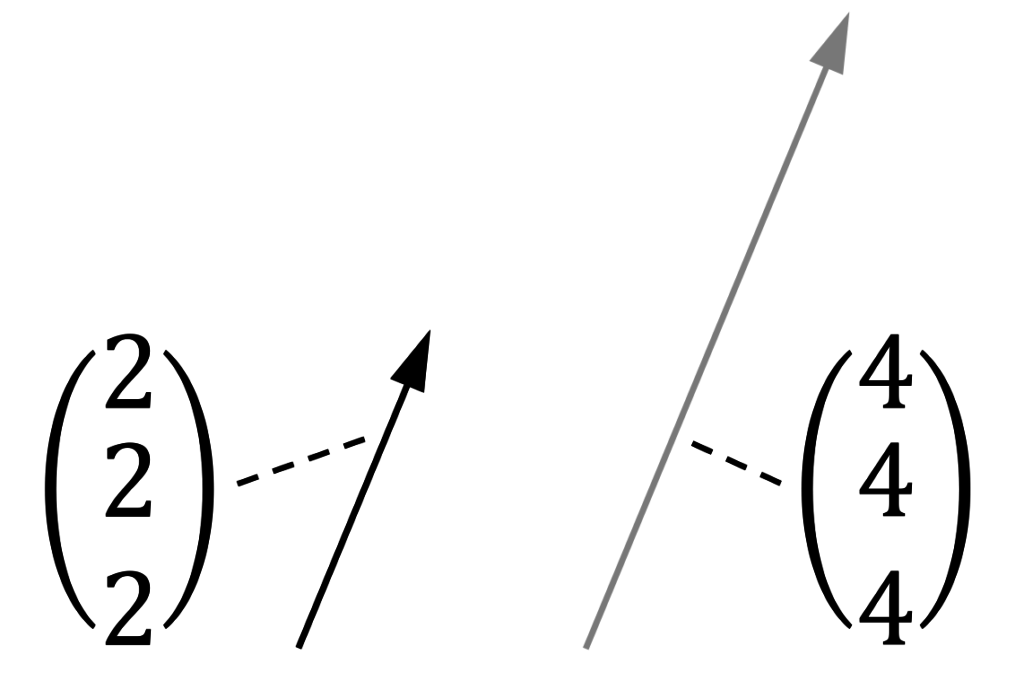
Beispiel mit zwei Vektoren Die zwei Vektoren $\vec{a}$ und $\vec{b}$ sind linear abhängig, da sie Vielfache voneinander sind (kollinear). Es gilt:
\begin{align*}
2 \cdot \left( \begin{array}{c} 2 \\ 2 \\ 2 \end {array} \right) =
\left( \begin{array}{c} 4 \\ 4 \\ 4 \end {array} \right) \notag
\end{align*}
Allgemeiner Ansatz bei der Untersuchung von zwei Vektoren aus $\mathbb{R}^2$:
\begin{align*}
\vec{a}= r \cdot \vec{b} \Rightarrow \left( \begin{array}{c} 4 \\ 4 \\ 4 \end {array} \right) = r \cdot \left( \begin{array}{c} 2 \\ 2 \\ 2 \end {array} \right) \Leftrightarrow \begin{array}{c} 4=2r \\ 4=2r \\ 4=2r \end {array} \Leftrightarrow \begin{array}{c} 2=r \\ 2=r \\ 2=r \end {array}
\end{align*}
Nun prüft man zeilenweise die Einträge und bestimmt jeweils $r$. Mögliche Lösungen:
- Wenn unterschiedliche Werte für $r$ rauskommen, dann sind die Vektoren nicht kollinear und damit linear unabhängig.
- Wenn für $r$ überall das Gleiche rauskommt, dann sind die Vektoren kollinear und linear abhängig.
Wenn wir zeigen müssen, ob drei Vektoren $\vec{a}$, $\vec{b}$ und $\vec{c}$ aus $\mathbb{R}^3$ linear abhängig sind oder nicht, sehen wir entweder auf Anhieb, ob sich einer der Vektoren aus den anderen Vektoren darstellen lässt (komplanar), siehe dazu das Beispiel mit zwei Vektoren, oder wir arbeiten mit dem allgemeinen Ansatz, welcher immer zum Erfolg führt:
\begin{align*}
r\cdot \vec{a}+s\cdot \vec{b}+t\cdot \vec{c} = \vec{0}
\end{align*}
Die zu untersuchende Gleichung ist äquivalent zu einem LGS, das man mit dem Gauß-Verfahren lösen kann. Mögliche Ergebnisse:
- $r=s=t=0$, dann sind die Vektoren nicht komplanar und damit linear unabhängig
- Wahre Aussage, z.B. $0=0$, dann sind die Vektoren komplanar und linear abhängig
Beispiel mit drei Vektoren Gegeben sind die Vektoren
\begin{align*}
\vec{a}=\left( \begin{array}{c} 1 \\ 1 \\ 2 \end {array} \right) \quad
\vec{b}=\left( \begin{array}{c} 3 \\ -1 \\ 1 \end {array} \right) \quad
\vec{c}=\left( \begin{array}{c} -1 \\ 3 \\ 3 \end {array} \right),
\end{align*}
die auf lineare Abhängigkeit untersucht werden sollen. Wir nehmen den allgemeinen Ansatz zur Hand und erhalten ein LGS, welches wir an dieser Stelle mit dem Gauß-Algorithmus (siehe Kap. LGS lösen) lösen:
\begin{align*}
r\cdot \vec{a}+s\cdot \vec{b}+t\cdot \vec{c} = \vec{0} \quad \Rightarrow \quad
\begin{array}{l} \textrm{I} \\ \textrm{II} \\ \textrm{III} \end{array} \left( \begin{array}{ccc|c} 1 & 3 & -1 & 0 \\ 1 & -1 & 3 & 0 \\ 2 & 1 & 3 & 0 \end {array} \right) \begin{array}{l} \\ \textrm{II}-\textrm{I} \\ \textrm{III}-2\cdot\textrm{I} \end{array}
\end{align*}
\begin{align*}
\Rightarrow \quad \left( \begin{array}{ccc|c} 1 & 3 & -1 & 0 \\ 0 & -4 & 4 & 0 \\ 0 & -5 & 5 & 0 \end {array} \right) \begin{array}{c} \\ \\ \textrm{III}-5/4\cdot \textrm{II} \end{array} \quad \Rightarrow \quad
\left( \begin{array}{ccc|c} 1 & 3 & -1 & 0 \\ 0 & -4 & 4 & 0 \\ 0 & 0 & 0 & 0 \end {array} \right)
\end{align*}
Interpretation des Ergebnisses: Da eine Nullzeile vorliegt, besitzt das LGS unendlich viele Lösungen. Hättet ihr das LGS mit einem anderem Verfahren aufgelöst, wäre eine wahre Aussage wie z.B. $0=0$ rausgekommen, was das gleiche bedeutet. Infolgedessen sind die Vektoren $\vec{a}, \ \vec{b}$ und $\vec{c}$ linear abhängig!
Merke beim Gauß-Verfahren:
- Nullzeile = Lineare Abhängigkeit
- keine Nullzeile = Lineare Unabhängigkeit
Koordinatenebenen
Als Koordinatenebene bezeichnet man eine von zwei Einheitsvektoren aufgespannte Ursprungsebene. Im dreidimensionalen Raum gibt es drei Koordinatenebenen: die $xy$-Ebene, die $xz$-Ebene und die $yz$-Ebene.
Im Folgenden seien die drei Koordinatenachsen des dreidimensionalen Raums $R^3$ mit $x_1$, $x_2$ und $x_3$ bezeichnet. Die drei Koordinatenebenen werden häufig mit den Buchstaben $E$ gekennzeichnet, der mit zwei Indizes versehen wird, die die beiden Einheitsvektoren angeben, von denen die Ebene aufgespannt wird:
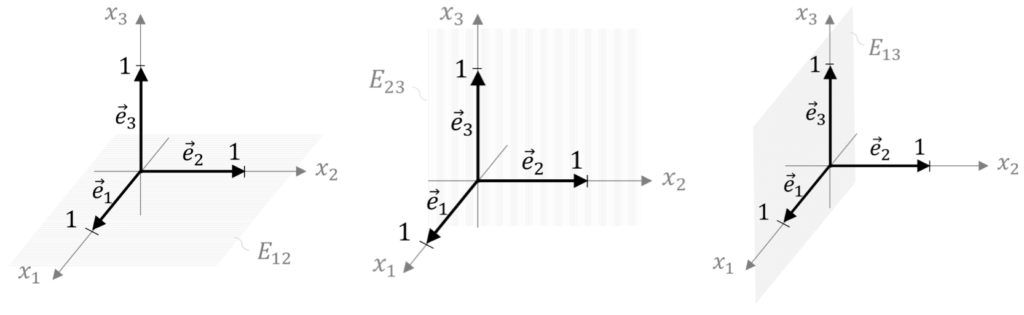
- die $x_1x_2$-Ebene $E_{12}$ wird von den Vektoren $\vec e_1$ und $\vec e_2$ aufgespannt
- die $x_1x_3$-Ebene $E_{13}$ wird von den Vektoren $\vec e_1$ und $\vec e_3$ aufgespannt
- die $x_2x_3$-Ebene $E_{23}$ wird von den Vektoren $\vec e_2$ und $\vec e_3$ aufgespannt
Hierbei sind die drei linear unabhängigen Einheitsvektoren $\vec e_1 = (1, 0, 0)^T$, $\vec e_2 = (0, 1, 0)^T$ und $\vec e_3 = (0, 0, 1)^T$.
Daniel erklärt dir das Thema Koordinatenebene nochmal in seinem Video

