
Wachstumsprozesse
Berechnungen zu Wachstum bzw. Wachstumsprozesse beschäftigen sich mit der Entwicklung von einem Bestand. Eine wichtige Idee dabei ist, dass die Änderung des Bestands (also Zunahme und Abnahme) die Ableitung des Bestands ist.
Inhaltsverzeichnis
- Lineare Wachstumsprozesse
- Exponentielle Wachstumsprozesse
- e-Funktion und Wachstumsprozesse
- Unbegrenzte Wachstumsprozesse
- Beschränkte Wachstumsprozesse
- Logistische Wachstumsprozesse
- Größerer Wachstums-/Zerfallszeitraum
Neu!
Lineare Wachstumsprozesse
Das lineare Wachstum ist sehr, sehr einfach. Es handelt sich hierbei um einen Bestand mit einer gleichmäßigen Entwicklung! Es kommt also in jeder Zeitspanne immer die gleiche Menge dazu (oder geht weg). Lineare Wachstumsprozesse werden durch Geraden beschrieben, der Ansatz lautet also:
\begin{align*}
y=m\cdot x+b \quad \textrm{oder auch} \quad B(t)=m\cdot t+b
\end{align*}
Beispiel
In einen Tümpel, der anfangs 200 m$^3$ dreckiges, stinkendes Wasser enthält, fließen täglich 4 m$^3$ sauberes, kristallklares Wasser dazu.
1. Wieviel Wasser enthält der See nach 50 Tagen?
Lineares Wachstum wird einfach durch unsere bekannte Geradengleichung beschrieben. Da Wachstumsprozesse meist von der Zeit $t$ (Englisch für „time“) abhängen, sehr ihr oft auch $B(t)=m\cdot t+b$. Hier hängt der Bestand $B$ von der Zeit $t$ ab. $b$ bezeichnet hierbei den Bestand zum Zeitpunkt 0, $m$ die Zunahme pro Zeiteinheit $t$. Unser Beispiel können wir also wie folgt beschreiben:
\begin{align*}
B(t)=4\cdot t+ 200 \quad [\textrm{m}^3]
\end{align*}
Um herauszufinden, wieviel Wasser nach 50 Tagen enthalten ist, setzen wir $t=50$ in die obige Gleichung ein und erhalten:
\begin{align*}
B(50)=4\cdot 50+ 200 =400 \ \textrm{m}^3
\end{align*}
Antwort: Nach 50 Tagen sind 400 m$^3$ in dem Tümpel.
2. Wann enthält der See 1000 m$^3$ Wasser?
Lösungsweg 1 – Überlegen: Zu Beginn waren schon 200 m$^3$ im Tümpel, also sind $1000-200=800$ m$^3$ hinzugekommen. Da 4 m$^3$ täglich hinzufließen, brauche ich 800/4=200 Tage, damit 1000 m$^3$ im Tümpel sind.
Lösungsweg 2 – Gleichung verwenden: Der Bestand $B$ soll 1000 m$^3$ sein. Also setzen wir die 1000 in die Geradengleichung ein und stellen nach der Unbekannten $t$ um. Es folgt:
\begin{align*}
B(t)&=4\cdot t+ 200 \\
1000&=4\cdot t+ 200 \quad \Rightarrow \quad t=200 \quad [\textrm{Tage}]
\end{align*}
3. Wann ist nur noch 1% des Wassers dreckig?
An dieser Stelle denken wir einmal nach und schauen uns den Aufgabentext an. Es fließt nur sauberes Wasser hinzu. Das einzig dreckige Wasser in dem Tümpel ist der Anfangsbestand. Demnach sind die gesuchten $1\%$ die anfänglichen $200$ m$^3$. Mit Hilfe des Dreisatz können wir herausfinden, dass $100\%$ also $20000$ m$^3$ sein müssen.
Jetzt stellt sich die Frage, wann $20000$ m$^3$ im Tümpel sind. Das können wir genau so wie Aufgabenteil 2. lösen. Wir verwenden hier den zweiten Lösungsweg und erhalten:
\begin{align*}
B(t)&=4\cdot t+ 200 \\
20000&=4\cdot t+ 200 \quad \Rightarrow \quad t=4950 \quad [\textrm{Tage}]
\end{align*}
Schau dir vertiefend das Lernvideo zum Thema Lineare Wachstumsprozesse an.
Exponentielle Wachstumsprozesse
Im vorherigen Kapitel haben wir gelernt, was es mit dem linearen Wachstum auf sich hat. Wir haben bewusst auf die Darstellung des linearen Zerfalls verzichtet, weil die Abläufe identisch sind. Der einzige Unterschied ist, dass etwas immer gleich viel abnimmt anstatt zunimmt.
Exponentielle Wachstumsprozesse sind Prozesse, in welchen die Zunahme (oder Abnahme) immer proportional zum Bestand ist, sprich: zum bereits vorhandenen Bestand kommt immer der gleiche prozentuale Anteil dazu (oder geht weg). Standardbeispiel: Zinsen bei der Bank (zu einem angelegten Kapital kommt immer der gleiche Zinssatz dazu).
Exponentielle Wachstumsprozesse werden durch die Funktionsgleichung
\begin{align*}
\textrm{Endwert} \ &= \ \textrm{Startwert} \cdot \textrm{Basis}^x \\
f(x) &= s \cdot b^x \\
f(t) &=a \cdot q^{t}
\end{align*}
mit
\begin{align*}
&q > 1 \ \textrm{als Wachstumsfaktor} \\
\textrm{und} \ &q < 1 \ \textrm{als Zerfallsfaktor}
\end{align*}
beschrieben.
Was bedeutet das jetzt? Hier ein paar Beispiele:
- 200 Fliegen verdoppeln täglich ihre Anzahl: $f(t) =200 \cdot 2^{t}$
- 200 Fliegen halbieren tägliche ihre Anzahl: $f(t) =200 \cdot 0,5^{t}$
- 200 Fliegen vermehren sich täglich um 7 $\%$. Allgemein: $f(t) =a \cdot \left(1+\frac{p}{100} \right) ^{t}$
\begin{align*}
f(t) =200 \cdot \left(1+\frac{7}{100} \right)^t = 200 \cdot 1,07^t
\end{align*}
- 200 Fliegen werden täglich 5 $\%$ weniger. Allgemein: $f(t) =a \cdot \left(1-\frac{p}{100} \right) ^{t}$
\begin{align*}
f(t) =200 \cdot \left(1-\frac{5}{100} \right)^t = 200 \cdot 0,95^t
\end{align*}
Die nachfolgende Abbildung soll euch als Übersicht zum Thema Wachstumsprozesse dienen. Hier sind lineare und exponentielle Prozesse gegenübergestellt, so dass die Unterschiede deutlich werden können.
Neu!
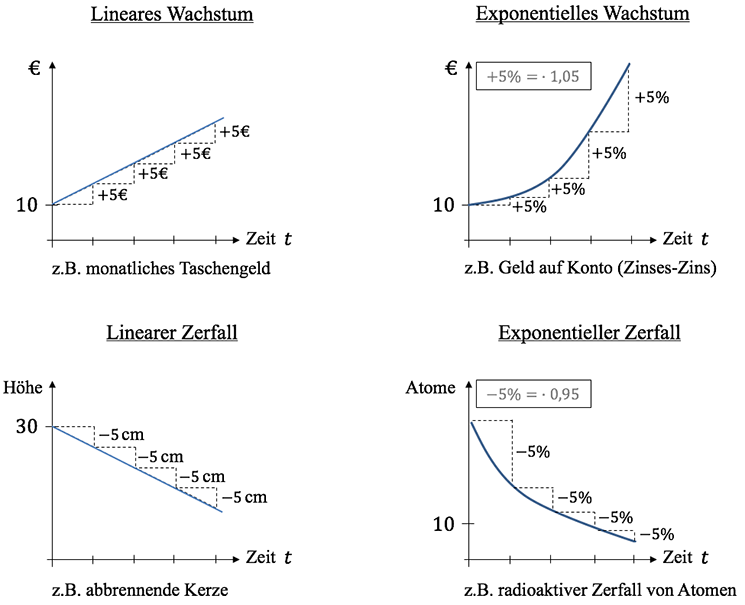
Typisch für exponentielle Wachstumsprozesse ist die Verdopplungszeit bzw. Generationszeit, wo gefragt wird, wann der doppelte Startwert (oder Anfangsbestand) erreicht wird und die Halbwertszeit (bei exponentieller Abnahme), wo gefragt wird, wann der halbe Startwert (oder Anfangsbestand) erreicht wird. Da bei der Verdopplungszeit immer nach dem doppelten Startwert ($2\cdot S$) mit $S$ als Startwert gefragt wird, steht auf der linken Seite der Gleichung immer eine 2 bzw. eine 0,5 bei der Halbwertszeit.
Beispiele:
Generationszeit:
\begin{align*}
f(t)&=200 \cdot 1,05^t \\
400&=200 \cdot 1,05^t \quad |:200 \\
2&=1,05^t \quad | \textrm{mit log} \\
t&=\log_{1,05}(2)
\end{align*}
Halbwertszeit:
\begin{align*}
f(t)&=200 \cdot 0,8^t \\
100&=200 \cdot 0,8^t \quad |:200 \\
0,5&=0,8^t \quad |\textrm{mit log} \\
t&=\log_{0,8}\left(0,5\right)
\end{align*}
e-Funktion und Wachstumsprozesse
Wenn die Basis der Exponentialfunktion die eulersche Zahl $e$ ist, dann sprechen wir im von DER Exponentialfunktion. Häufig wird bei Aufgaben zu Wachstums- oder Zerfallsprozessen die Basis $e$ gewählt. Die allgemeine Form lautet:
\begin{align*}
f(t)&=a\cdot e^{\pm k\cdot t} \\
\textrm{mit} \quad \quad k&=ln(1+\frac{p}{100} ) \quad \textrm{als Wachstumskonstante und} \\
k&=ln(1-\frac{p}{100} ) \quad \textrm{als Zerfallskonstante.}
\end{align*}
Exponentialfunktion aufstellen mit 2 Punkten
Häufig sind die Aufgaben bei Wachstumsprozessen so gestellt, dass aus dem Aufgabentext zwei Punkte herausgefunden werden müssen und man aus diesen zwei Punkten eine Exponentialfunktion aufstellen muss. Dazu gucken wir uns direkt mal ein typisches Beispiel an.
Beispiel:
Daniel hat einen normalen Hormonspiegel von 6 mg/l. Als er Chantal zum ersten Mal sieht, schnellt der Hormonspiegel innerhalb 3 Minuten auf 9 mg/l hoch. Wie hoch ist der Hormonspiegel nach einer Viertelstunde, wenn man von einer Entwicklung gemäß $h(t)=a\cdot e^{kt}$ ausgehen kann?
Wie gehen wir vor? Die Form der Funktion, hier Exponentialfunktion, ist bereits gegeben. Folgende Infomationen müssen aus der Aufgabenstellung herausgezogen werden:
\begin{align*}
t&=0: \ h(0)=6 \quad \textrm{daraus folgt der Punkt} \ P_1(0|6)\\
t&=3: \ h(3)=9 \quad \textrm{daraus folgt der Punkt} \ P_2(3|9) \\
\end{align*}
Gesucht ist der Hormonspiegel nach einer Viertelstunde, also $h(15)=?$.
Aus $P_1(0|6)$ und $P_2(3|9)$ folgen dann zwei Gleichungen, die wir nach den uns bekannten Verfahren nach den beiden Unbekannten $a$ und $k$ auflösen.
\begin{align*}
\textrm{I} \quad 6&=a \cdot \underbrace{e^{k\cdot 0}}_{=1} \\
\textrm{II} \quad 9&=a \cdot e^{k\cdot 3}
\end{align*}
Aus Gleichung $\textrm{I}$ folgt direkt $a=6$ und das setzen wir in Gleichung $\textrm{II}$ ein und erhalten:
\begin{align*}
9 & =6 \cdot e^{k\cdot 3} \quad |:6 \\
\Leftrightarrow \quad 1,5 &= e^{3k} \quad |\ \ln \\
\Rightarrow \quad \ln(1,5) &= 3k \quad |:3 \\
\Leftrightarrow \quad k &= \frac{\ln(1,5)}{3} \approx 0,135
\end{align*}
Damit folgt für die gesuchte Wachstumsfunktion: $h(t)=6\cdot e^{0,135 \cdot t}$. Wenn Ihr die Funktion habt, ist der Rest meist einfach. Daniel hat nach 15 Minuten einen Hormonspiegel von
\begin{align*}
h(15)=6\cdot e^{0,135 \cdot 15} \approx 45,46 \ \frac{\textrm{mg}}{\textrm{l}}.
\end{align*}
Beachtet bitte, dass die Rundungsfehler bei $e$-Funktionen sehr hoch sind.
Daniel erklärt dir nochmals alles zum Thema exponentielle Wachstumsprozesse in seinem Lernvideo.
Unbegrenzte Wachstumsprozesse bzw. unbegrenzter Zerfall
In diesem Abschnitt sollt ihr eine Übersicht zu unbegrenztem Wachstum/Zerfall bekommen. Wir haben $N(t)$ als den $y$-Wert, der rauskommt, wenn ich einen Anfangswert
$N(0)$ mal $e^{k\cdot t}$ habe. $k$ muss dabei größer als Null sein. Dabei ist es egal, ob Wachstum oder Zerfall vorliegt.
Unbegrenztes Wachstum:
\begin{align*}
N(t)&=N(0)\cdot e^{k\cdot t} \\
N'(t)&=k \cdot N(0)\cdot e^{k\cdot t} \\
&=k \cdot N(t)
\end{align*}
Verdopplungszeit: $t=\frac{\ln(2)}{k}$
Unbegrenzter Zerfall:
\begin{align*}
N(t)&=N(0)\cdot e^{-k\cdot t} \\
N'(t)&=-k \cdot N(0)\cdot e^{-k\cdot t} \\
&=-k \cdot N(t)
\end{align*}
Halbwertszeit: $t=\frac{\ln(0,5)}{-k}$
Beispiel zur Halbwertszeit
In lebenden Organismen beträgt der Anteil des Kohlenstoffisotops C14 etwa ein Billionstel aller Kohlenstoffatome. In abgestorbenen Organismen zerfällt das C14-Isotop exponentiell. Nach 1000 Jahren sind noch ca. 0,886 Billionstel vorhanden. Bestimme die Halbwertszeit von C14.
Es liegt ein unbegrenzter Zerfall vor. Unser Ansatz lautet zunächst $N(t)=N(0)\cdot e^{-kt}$. Wir müssen also den Anfangswert $N(0)$ und $k$ bestimmen.
2 Informationen sind im Aufgabentext gegeben, um gesuchten Werte zu bestimmen:
- Anfangswert: $N(0)=1$
- Nach 1000 Jahren: $N(1000)=0,886$
Hinweis: Die Einheit ist Billionstel. Wir erhalten
\begin{align*}
0,886&=1\cdot e^{-k\cdot 1000} \quad | \ln \\
\ln(0,886)&=-k\cdot 1000 \\
k&=0,000121
\end{align*}
und damit die Funktion, die den unbegrenzten Verfall beschreibt: $N(t)=1\cdot e^{-0,000121\cdot t}$.
Erst jetzt beginnen wir mit der Fragestellung. Wir verwenden einfach die Formel von oben und es folgt für die Halbwertszeit:
\begin{align*}
t=\frac{\ln(0,5)}{-0,000121} \approx 5728 \ \textrm{Jahre}
\end{align*}
Schau dir hierzu das Lernvideo zum Thema exponentielle, unbegrenzte Wachstumsprozesse an!
Beschränkte Wachstumsprozesse und beschränkte Abnahme
Grundsätzlich unterscheidet man zwischen beschränktem Wachstum und beschränkter Abnahme. Ganz allgemein gilt mit $k>0$, $s \in \mathbb{R}$ und $t$ für die Zeit.:
\begin{align*}
f(t) = S\pm c \cdot e^{-k\cdot t}
\end{align*}
Beschränkter Wachstumsprozess:
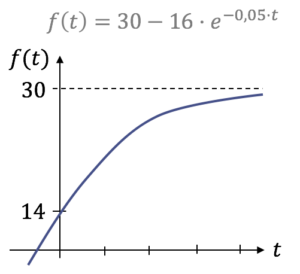
Beispiel für beschränktes Wachstum: Ihr holt ein Glas Milch aus dem Kühlschrank und stellt es in euer Zimmer. Wir haben eine Zunahme der Temperatur, die beschränkt ist auf die Raumtemperatur.
Beschränkte Abnahme
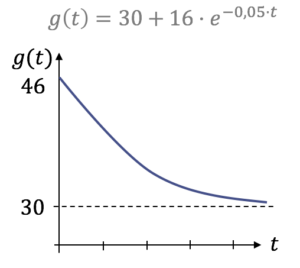
Beispiel für beschränkte Abahme: Ihr erhitzt ein Glas Milch und stellt es in euer Zimmer. Wir haben eine Abnahme der Temperatur, die beschränkt ist auf die Raumtemperatur.
Charakteristisch für beschränktes Wachstum oder beschränkte Abnahme ist, dass die Steigung mit steigender Zeit abnimmt. Unterschied zu logistischem Wachstum!
Sieh dir zur Vertiefung Daniels Video zum Thema beschränkte Wachstumsprozesse an.
Logistische Wachstumsprozesse
Ähnlich wie beim beschränkten Wachstum erkennt ihr, wenn man nach rechts schaut, die Steigung des Graphen immer weiter abnimmt bis sie 0 ist und sich einem Grenzwert asymptotisch annähert. Anders als beim beschränkten Wachstum ist es aber so, dass die Wachstumsgeschwindigkeit zu Beginn zunimmt, bevor sie abnimmt. In der Abbildung seht ihr eine Beispiel, wie ein logistisches Wachstum graphisch aussehen könnte.
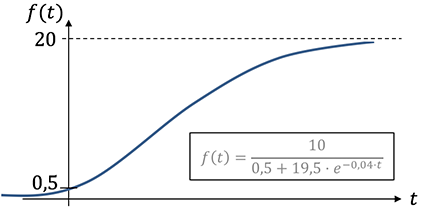
Wie kommt man auf den Grenzwert (Schranke $S$), der hier 20 ist? Einfach ausgedrückt: Zahl oben durch Zahl, die alleine steht, ist die sogenannte Schranke, bei der sich der Graph vom Wert her einpendelt. In unserem Beispiel: $10/0,5=20$.
Die Zahl, die unter dem Bruchstrich alleine steht, ist zeitgleich der Schnittpunkt mit der $y$-Achse. Hier: $0,5.$ Damit hat man alle Sonderheiten geklärt.
Allgmein gilt für logistisches Wachstum folgende Gleichung:
\begin{align*}
f(t) = \frac{a\cdot S}{a+(S-a)\cdot e^{-S kt} },
\end{align*}
wobei $a=f(0)$, $0<a<S$, $k>0$ und $S>0$.
Größerer Wachstums-/Zerfallszeitraum
Wenn ein größerer Zeitraum als \textit{täglich, stündlich, minütlich} vorgegeben ist, z.B. alle 4 Tage werden 200g 20\% mehr, habt ihr zwei Möglichkeiten, die Exponentialfunktion aufzustellen:
Möglichkeit 1:
Richtigen Wachstumsfaktor ausrechnen!
\begin{align*}
f(x)&=200 \cdot q^x \\
\underbrace{240}_{200+20\%}&=200 \cdot q^4 \quad |:200 \\
1,2&=q^4 \quad \quad \quad \ | \textrm{4. Wurzel ziehen} \\
q&=\sqrt[4]{1,2} \\
\Rightarrow \ f(x)&=200 \cdot \left( \sqrt[4]{1,2} \right)^x
\end{align*}
Möglichkeit 2:
Exponenten anpassen!
\begin{align*}
f(x)&=200 \cdot (\underbrace{1,2}_{1+\frac{0,2}{100}})^{\frac{1}{4}x} \\
&=200 \cdot \left(1,2^{\frac{1}{4}} \right)^x \\
&=200 \cdot \left( \sqrt[4]{1,2} \right)^x
\end{align*}
Neu!

