
Das Zufallsexperiment
Auf dieser Seite erfährst du alles zum Thema Zufallsexperiment. Wir vertiefen im Folgenden diese Themen:
- Ergebnis, Ereignis und Ereignisraum
- Verknüpfungen von Ereignissen
- Der Wahrscheinlichkeitsbegriff
- Wahrscheinlichkeit nach Laplace
Neu!
Bei einem Zufallsexperiment (auch Zufallsversuch genannt) handelt es sich um einen Versuch, der unter bestimmten Bedingungen durchgeführt wird und einen zufälligen Ausgang besitzt. Eigenschaften eines Zufallsexperimentes sind:
- geplant und kontrolliert ablaufender Zufallsvorgang
- wiederholbar unter gleichen Bedingungen
- mögliche Ergebnisse des Vorgangs stehen im Voraus fest
- Das tatsächliche Ergebnis ist im Voraus nicht bekannt.
- Beispiele: Werfen eines Würfels, Ziehung der Lottozahlen
Schau dir zur Einleitung in das Thema Zufallsexperiment Daniels Lernvideo an.
Ergebnis, Ereignis und Ereignisraum
Ein Elementarereignis ist ein einzelnes und sich gegenseitig ausschließendes mögliches Ergebnis $\omega$ eines Zufallsexperimentes. Wenn wir einen Würfel einmal werfen, gibt es nur folgende Möglichkeiten, wie der Würfel fallen kann:
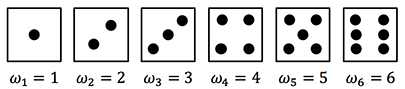
Die Menge aller möglichen Ergebnisse $\omega_i$ heißt Ergebnisraum $\Omega$, wobei jedes Ergebnis genau einmal in $\Omega$ vorkommt. Für unser Beispiel mit dem einmaligen Werfen eines Würfels folgt für den Ergebnisraum:
\begin{align*}
\Omega=\{\omega_1,\omega_2,\omega_3,\omega_4,\omega_5,\omega_6 \} = \{1,2,3,4,5,6\}
\end{align*}
Jede Zusammenfassung von einem oder mehreren Ergebnissen eines Zufallsexperimentes in einer Menge wird Ereignis genannt.
Beispiele für Ereignisse:
- eine ungerade Zahl beim Drehen eines Glücksrades (1-9) – Lösung: $\{ 1,3,5,7,9\}$
- Werfen von zwei Würfeln, deren Augenzahlsumme 10 ist – Lösung: $\{ (6;4),(5;5),(4;6) \}$
Spezielle Ereignisse sind das sichere und das unmögliche Ereignis.
Sicheres Ereignis: Die Ergebnismenge $\Omega$ ist die Zusammenfassung aller möglichen Ergebnisse eines Zufallsexperimentes. Sie ist somit ebenfalls ein Ereignis. Da dieses Ereignis immer eintritt, nennt man dieses Ereignis auch sicheres Ereignis.
Beispiel: Beim Zufallsexperiment Zweimaliges Werfen eines Würfels ist das Ereignis Summe der beiden Augenzahlen ist kleiner oder gleich 12 ein sicheres Ereignis!
Unmögliches Ereignis: Das unmögliche Ereignis ist ein Ereignis, das bei jeder Ausführung des Zufallsexperimentes niemals eintreten kann. Die Wahrscheinlichkeit für das Eintreten jedes unmöglichen Ereignisses ist also gleich Null!
Beispiel 1: Beim Zufallsexperiment Zweimaliges Werfen eines Würfels ist das Ergebnis Summe der beiden Augenzahlen ist gleich Null unmöglich.
Beispiel 2: Beim Würfeln eines normalen Würfels eine 7 würfeln.
Neu!
Verknüpfungen von Ereignissen
Durch Verknüpfung von Ereignissen entstehen zusammengesetzte Ereignisse. Diese werden häufig anhand von Venn-Diagrammen veranschaulicht. Letztere bestehen aus einem Rechteck, in dem die Ausgangsereignisse (Mengen $A$, $B$,…) als Kreise oder Ellipsen dargestellt sind.

Schau dir zur Vertiefung nochmals das Lernvideo zu „rechnen mit Mengen“ an.
Der Wahrscheinlichkeitsbegriff
Den einzelnen Elementen eines Ereignisraumes lassen sich Wahrscheinlichkeiten zuordnen. Die Wahrscheinlichkeit eines Ereignisses $A$ wird mit $P(A)$ bezeichnet.
Bei einem Zufallsexperiment kann man zwar nicht voraussagen, welches Ereignis eintritt, man hält jedoch oft das Eintreten einiger Ereignisse für mehr, andere für weniger wahrscheinlich.
Eigenschaften:
- $0 \leq P(A) \leq 1$
- $P(\Omega) = 1$ (Normierung) und $P(\{ \}) = 0$
- $P(A \cup B) = P(A) + P(B) – P(A\cap B)$ (Additionssatz)
- $P(\overline{A})=1-P(A) $ (Gegenwahrscheinlichkeit)
Die Wahrscheinlichkeit ordnet jedem Ereignis eine nicht-negative Zahl zu. Weitere nützliche Zusammenhänge:
$P(A \cup B \cup C)$=$P(A)+P(B)+P(C) -P(A \cap B)-P(B \cap C)-P(A \cap C) \ +P(A \cap B \cap C)$
$P(A\backslash B)$=$P(A)-P(A \cap B)$ (Wahrscheinlichkeit der Differenzmenge)
Daniel erklärt euch in diesem Lernvideo nochmals die Grundlagen zum Thema Wahrscheinlichkeit
Wahrscheinlichkeit nach Laplace
Um Wahrscheinlichkeiten berechnen zu können, benötigt man Zusatzinformationen über das jeweilige Zufallsexperiment. Eine Zusatzinformation kann z.B. darin bestehen, dass man weiß, dass die Ergebnismenge endlich (oder auch abzählbar) ist und die Wahrscheinlichkeiten für die n Elementarereignisse alle gleich groß sind. Ein Zufallsexperiment mit diesen Eigenschaften heißt Laplace-Experiment. Bei einem Laplace-Experiment lässt sich die Wahrscheinlichkeit für ein Ereignis $A$ als Quotient aus der Anzahl der für $A$ günstigen Fälle und der Anzahl aller möglichen Ergebnisse des Zufallsexperiments errechnen:
\begin{align*}
P(A) = \frac{\textrm{Anzahl der Elementarereignisse, bei denen A eintritt}}{\textrm{Anzahl aller überhaupt möglichen Elementarereignisse}} \notag
\end{align*}
Beispiele
1. Wie hoch ist beim zweimaligen Würfeln die Wahrscheinlichkeit, dass die Augensumme 7 beträgt?
Wie wir bereits wissen, müssen wir zunächst alle möglichen Ereignisse (Elementarereignisse) auflisten. Die Elementareignisse lauten zusammengefasst in unserem Ereignisraum:
\begin{align*}
\Omega = \{ &(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6), \\
&(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6), \\
&(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6) \}
\end{align*}
Es gibt also generell 36 Möglichkeiten, wie die Würfel bei zweimaligem Werfen fallen können. Als Nächstes markieren wir uns die Ereignisse, die für uns von Interesse sind:
\begin{align*}
A=\{(1,6), (2,5), (3,4), (4,3), (5,2), (6,1) \}
\end{align*}
Demnach sind sechs günstige Ereignisse für uns von Interesse! Merke: Das für uns günstige Ereignis $A$ muss eine Teilmenge aller möglichen Ereignisse sein, kurz: $A \subset \Omega$. Wenn wir jetzt noch die Anzahl der günstigen Ereignisse durch die Anzahl der möglichen teilen, erhalten wir die gesuchte Wahrscheinlichkeit:
\begin{align*}
P(A) = \frac{6}{36}=\frac{1}{6}
\end{align*}
2. Ereignis, dass bei einmaligem Würfeln eine sechs auftritt.
- $\Omega = \{ 1,2,3,4,5,6 \}$ (mögliche Ereignisse)
- Ereignis: $A = \{6\}$
- Wahrscheinlichkeit: $P(A)=\frac{1}{6}$
3. Ereignis, dass bei einmaligem Würfeln nur gerade Zahlen erscheinen.
- $\Omega = \{ 1,2,3,4,5,6 \}$
- Ereignis: $A = \{2,4,6\}$
- Wahrscheinlichkeit: $P(A)=\frac{3}{6}=\frac{1}{2}$
4. Ereignis, dass bei einmaligem Würfeln nur eine zwei oder eine vier gewürfelt wird.
- $\Omega = \{ 1,2,3,4,5,6 \}$
- Ereignis: $A = \{2,4\}$
- Wahrscheinlichkeit: $P(A)=\frac{2}{6}=\frac{1}{3}$
Schau dir nochmal zur Wiederholung das Lernvideo zum Thema Stochastik Grundlagen an.
Alles zum Thema Stochastik findest du in Daniels Playlist.

