Auflagerreaktionen
In diesem Artikel erklären wir dir anhand von Erklärungen, Videos und Beispielen alles zum Thema Auflagerreaktionen bestimmen. Wir gehen dabei auf folgende Themen ein:
19,99€
Definition
„Eine Auflagerreaktion ist eine Kraft oder ein Moment, mit der ein Auflager oder eine Einspannung ein technisches Objekt wie zum Beispiel ein Tragwerk stützt. Die Gesamtheit der Auflagerreaktionen fixiert das jeweilige Objekt auf den Auflagern.“[2]
[2] https://de.wikipedia.org/wiki/Auflagerreaktion
Belastungen
Hier möchten wir euch einen Überblick über typische Belastungsarten geben und wie ihr damit umgehen müsst.
1. Kräfte: Kräfte können horizontal oder vertikal am System angreifen. Es kann auch passieren, dass sie unter einem bestimmten Winkel (hier: $\alpha$) angreifen. Dann könnt ihr die Kraft in eine horizontale und vertikale Komponente mit Hilfe von Sinus und Kosinus aufteilen.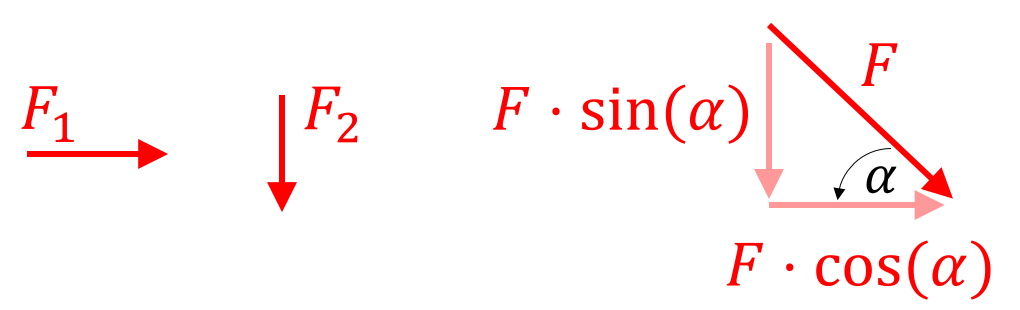
2. Momente: Momente greifen im oder gegen den Uhrzeigersinn an und können in ihrer Wirkungsebene beliebig verschoben werden. Für äußere Momente verwenden wir einen Oberstrich – innere Momente haben keinen Oberstrich.
3. Streckenlasten: Können in unterschiedlichsten Formen auftreten. Wenn Auflagerreaktionen berechnet werden sollen, könnt ihr die Streckenlast durch eine Resultierende ersetzen. So ist die Berechnung kinderleicht. Merkt euch: Die Resultierende greift immer im Schwerpunkt an. Der Betrag der Resultierenden ist nichts anderes als der Flächeninhalt dieser Streckenlast. Bei komplizierten Geometrien bzw. wenn Funktionen angegeben sind, muss der Flächeninhalt mittels Integration berechnet werden. Bei folgenden Beispielen geht es auch einfacher:
- Rechteckige Streckenlast:
- Schwerpunkt in der Mitte
- Flächeninhalt: „Breite $l$ mal Höhe $q_0$“
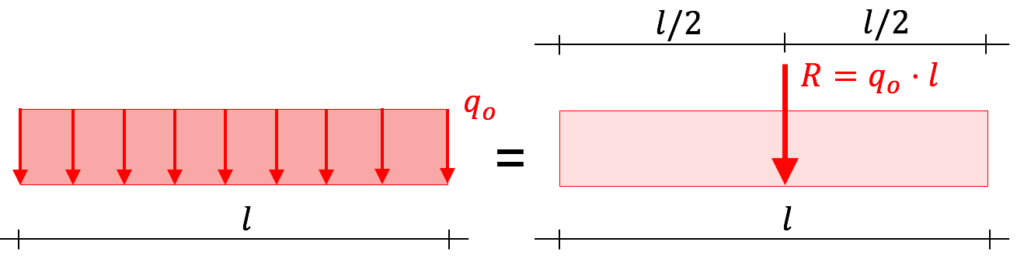
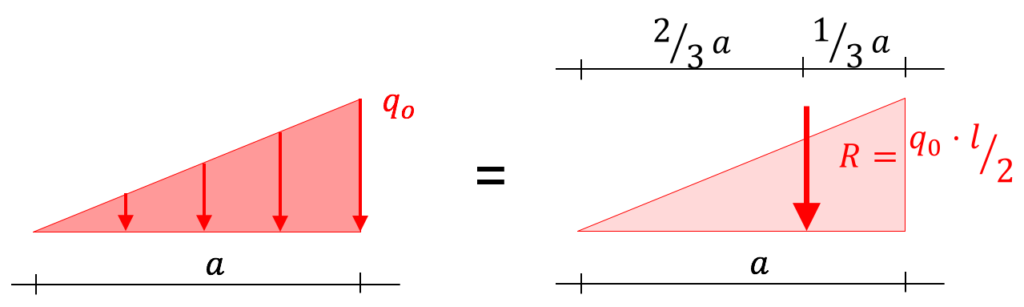
- Dreieckige Streckenlast:
- Schwerpunkt bei 2/3 – 1/3 der Gesamtlänge
- Flächeninhalt: „(Breite $l$ mal Höhe $q_0$)/2“
Video zu Resultierende einer Streckenlast
Neu!
Berechnung der Auflagerreaktionen
Vorgehen:
1) Freischnitt machen – damit können innere Kräfte sichtbar gemacht werden! Hier eine Übersicht der drei typischsten Lagertypen in der Mechanik: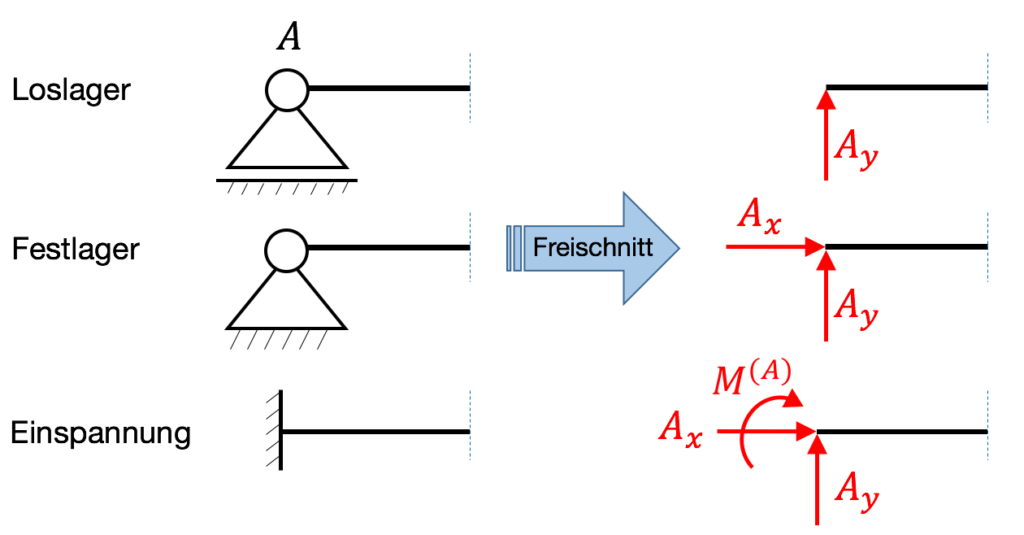
Hinweis zur Bezeichnung der Reaktionskräfte: Oft wird anstelle des Index x ein H für Horizontal und anstelle von y ein V für Vertikal verwendet.
Video zu den verschiedenen Lagerarten
Neu!
2) Gleichgewichtsbedingungen (GGB) aufstellen
(i) 2-dimensional: max. 3 unabhängige GGB pro System!
Z.B. können folgende GG aufgestellt werden:
a) Summe der Kräfte in horizontaler Richtung
Schreibweise: $\rightarrow:$ oder $\sum_1^i F_xi:$
b) Summe der Kräfte in vertikaler Richtung
Schreibweise: $\uparrow:$ oder $\sum_1^i F_yi:$
c) Summe der Momente um einen beliebigen Punkt
Schreibweise: $\stackrel{\curvearrowleft}{P}:$ Summe der Momente um Bezugspunkt $P$ oder $\sum_{i=1}^{n} M_{i}(P) = 0$
Beachte: Es kann auch vorteilhaft sein, nur Momentengleichgewichte aufzustellen!
(ii) 3-dimensional: max. 6 unabhängige GGB pro System!
Z.B. Kräfte-Gleichgewicht in bestimmte Achsenrichtung bilden oder um eine bestimmte Achse drehen.
Beispielaufgaben mit Lösungen
Beispiel einteiliges System
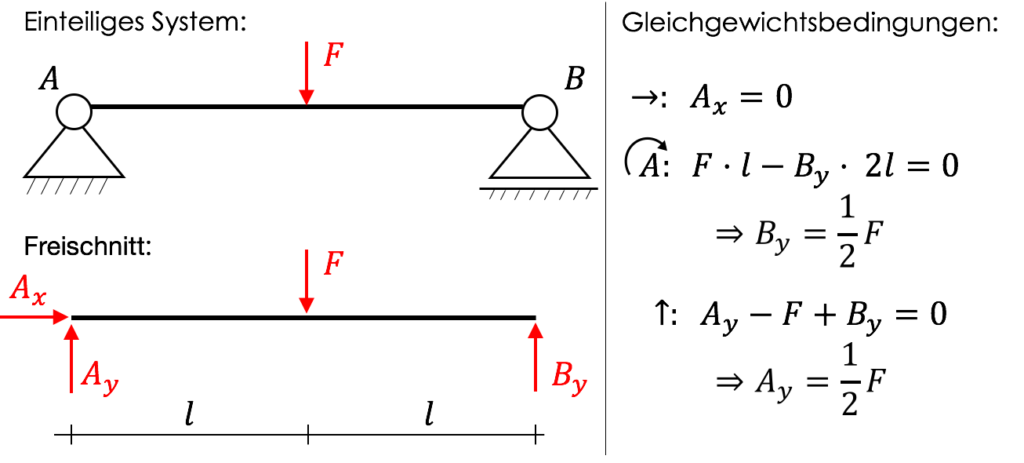
Beispiel einteiliges System mit Streckenlast
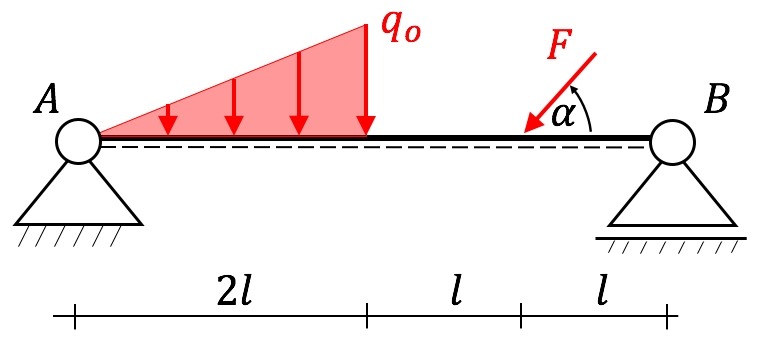
Bestimme die Lagerreaktionen des nachfolgenden statisch bestimmten Systems. Bekannt: $F,\ q_0,\ l $
Wie immer das Wichtigste zuerst: Freischnitt! Die dreieckige Streckenlast haben wir durch die Resultierende ersetzt, welche im Schwerpunkt des Dreiecks angreift. Auch die schräg angreifende Kraft haben wir in die horizontale und vertikale Komponente aufgeteilt.
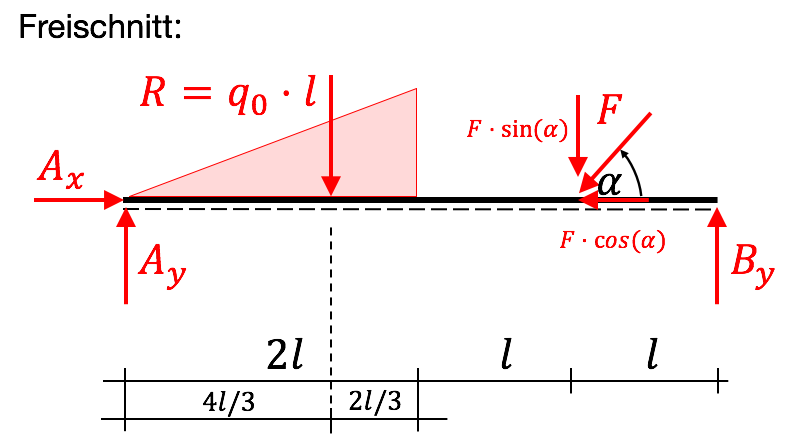
Nun gilt es, die Unbekannten möglichst clever zu bestimmen. Hier ein Vorschlag:
\begin{align*}
\rightarrow: \ A_x – F\cdot \cos (\alpha)=0 \quad &\Leftrightarrow \quad A_x=F\cdot \cos (\alpha) \\
\stackrel{\curvearrowright}{A}: \ R\cdot \frac{4l}{3} + F\cdot \sin (\alpha)\cdot 3l – B_y \cdot 4l=0 \quad &\Leftrightarrow \quad B_y = \frac{R}{3}+ \frac{3F\cdot \sin (\alpha)}{4} \\
\stackrel{\curvearrowleft}{B}: \ R\cdot \frac{8l}{3} + F\cdot \sin (\alpha)\cdot l – A_y \cdot 4l=0 \quad &\Leftrightarrow \quad A_y = \frac{2R}{3}+ \frac{F\cdot \sin (\alpha)}{4}
\end{align*}
Damit haben wir unsere Unbekannten bestimmt. Bisher haben wir alles symbolisch gerechnet, also ohne Zahlenwerte. Wer das kann, kann am Ende auch die Zahlen in den Taschenrechner eingeben!
Beispiel mehrteiliges System
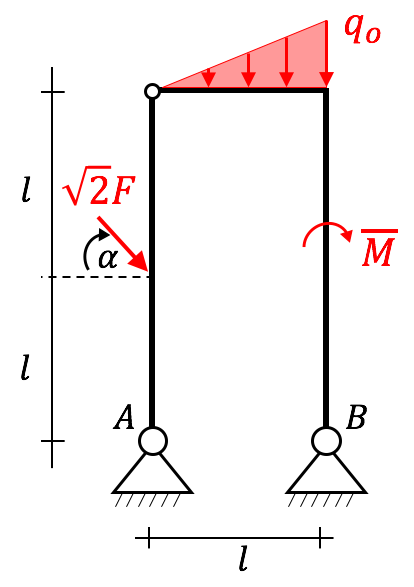
Bestimme die Lagerreaktionen des nachfolgenden statisch bestimmten mehrteiligen Systems. Bekannt: $\overline{M}=2Fl, \ F, \ q_0=4F/l, \ l$
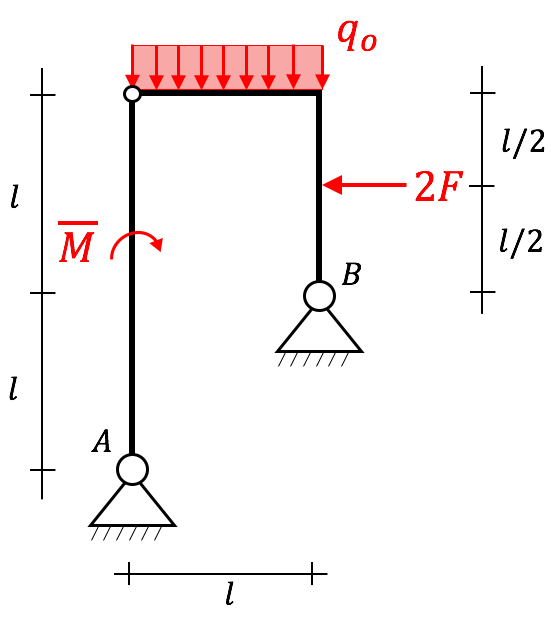Bei mehrteiligen Systemen ist es hilfreich, mehrere Freischnitte zu machen. Für dieses Beispiel erhalten wir 3 Freischnitte (Gesamtsystem GS, Teilsysteme TS 1 und 2), mit denen wir arbeiten können.
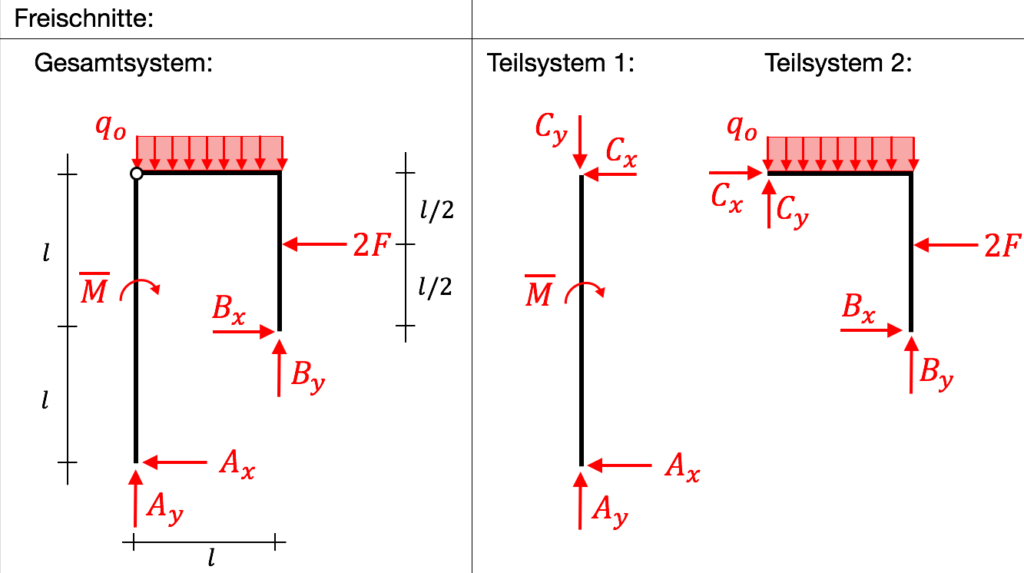
Hier ein Lösungsvorschlag, wie man das Ganze halbwegs elegant lösen kann. Beachte: Wie wir die Richtung der Lagerkräfte eintragen, ist komplett egal! Wir erhalten am Ende lediglich ein unterschiedliches Vorzeichen. Mit dem Gesamtsystem kann man jetzt noch nichts anfangen. Daher schauen wir uns zunächst das TS 1 an.
\begin{align*}
\stackrel{\curvearrowright}{C}: \ A_x \cdot 2l + \overline{M}=0 \quad &\Leftrightarrow \quad A_x= -\frac{\overline{M}}{2l}= -F \\
\leftarrow: \ A_x +C_x =0 \quad &\Leftrightarrow \quad C_x= – A_x = F
\end{align*}
Mit TS 1 kommen wir an dieser Stelle nicht weiter, weshalb wir uns nun TS 2 angucken.
\begin{align*}
\stackrel{\curvearrowright}{B}: \ C_x \cdot l + C_y \cdot l – q_0\cdot l \cdot \frac{l}{2}-2F\cdot \frac{l}{2}=0 \quad &\Leftrightarrow \quad C_y= q_0 \cdot \frac{l}{2} + F – C_x=2F \\
\uparrow: \ C_y – q_0\cdot l+B_y=0 \quad &\Leftrightarrow \quad B_y= q_0 \cdot l – C_x= 2F \\
\rightarrow: \ C_x – 2F +B_x=0 \quad &\Leftrightarrow \quad B_x= 2F – C_x= F
\end{align*}
Zu guter Letzt betrachten wir das Gesamtsystem, um die letzte Unbekannte $A_y$ zu bestimmen. Wir erhalten:
\begin{align*}
\uparrow: \ A_y – q_0\cdot l+B_y=0 \quad \Leftrightarrow \quad A_y= q_0 \cdot l – B_y= 2F
\end{align*}
Damit sind alle Unbekannten bestimmt und die Aufgabe ist gelöst!
Aufgabe mehrteiliges System
Bestimme die Lagerreaktionen des nachfolgenden statisch bestimmten mehrteiligen Systems. Bekannt: $\overline{M}=2Fl,\ F,\ q_0=\frac{F}{l}, \ l, \ \alpha=45^o$
Lösungsvideo zur Aufgabe
19,99€