
Fachwerk
Du willst wissen wie du Fachwerke richtig berechnest? In diesem Artikel zeigen wir dir anhand von Erklärungen, Videos und Übungsaufgaben die wichtigsten Schritte. Wir gehen dabei auf folgende Themen ein:
- Allgemeines zur Berechnung von Fachwerken
- Ermittlung von Nullstäben
- Ermittlung der Stabkräfte
- Beispielaufgaben zur Fachwerksberechnung

19,99€
Allgemeines zur Berechnung von Fachwerken
Das Besondere an Fachwerken ist, dass nur Kräfte in Stabrichtung (keine Querkräfte/Momente) vorliegen. Das Stichwort: Pendelstäbe!
Zusätzlich liegen in den einzelnen Knoten zentrale Kraftsysteme vor, was die Berechnung vereinfacht. Zudem kann die Untersuchung der Freiheitsgrade und des Gleichgewichts auf Knoten reduziert werden. Die Freiheitsgrade eines Knotens in der Ebene haben den Wert: $f=2$, also keine Verdrehung!
Was behindert also die Verschiebung des Knotens?
- Anzahl der Stäbe $s$
- Lagerreaktionen $r$
Die Untersuchung der statischen Bestimmtheit findet ihr im Kapitel statische Bestimmtheit.
Es sollte beachtet werden, dass äußere Kräfte i.d.R. nur an Knoten angreifen.
Ermittlung von Nullstäben
Nachdem die Statische Bestimmtheit geprüft ist und Stabkräfte berechnet werden sollen, ist es vorteilhaft, sich zunächst die Nullstäbe rauszusuchen. Das kann man mit etwas Übung sehr leicht sehen. Allerdings bedarf es dann einer guten Begründung!
Die Begründung kann dabei mittels der drei nachstehenden Regeln oder über den Kräfte- & Lageplan (KP & LP) erfolgen!
Regel 1:
„Sind an einem unbelasteten Knoten 2 Stäbe angeschlossen, die nicht in gleicher Richtung liegen, so sind diese Stäbe Nullstäbe.“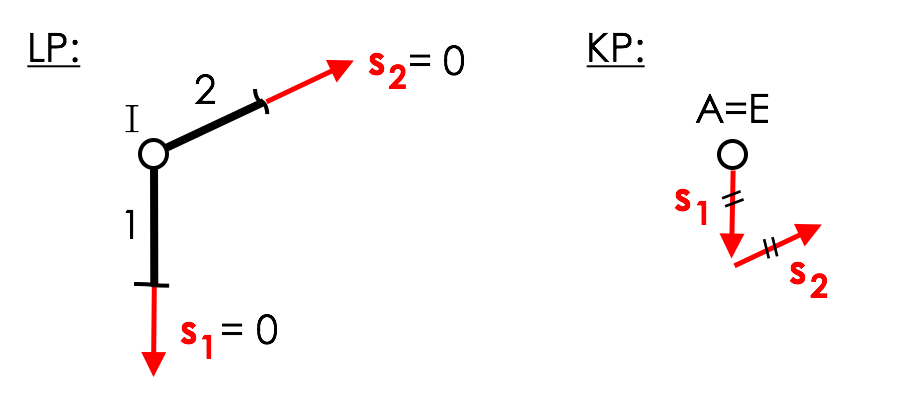
Regel 2:
„Sind an einem belasteten Knoten 2 Stäbe angeschlossen und liegt die Last in Richtung einer dieser Stäbe, so ist der andere ein Nullstab.“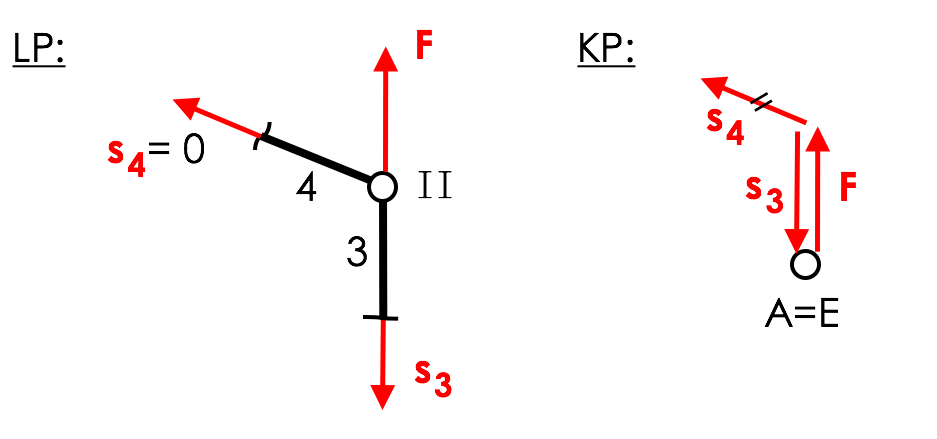
Regel 3:
„Sind an einem unbelasteten Knoten 3 Stäbe angeschlossen, von denen zwei in gleicher Richtung liegen, so ist der dritte ein Nullstab.“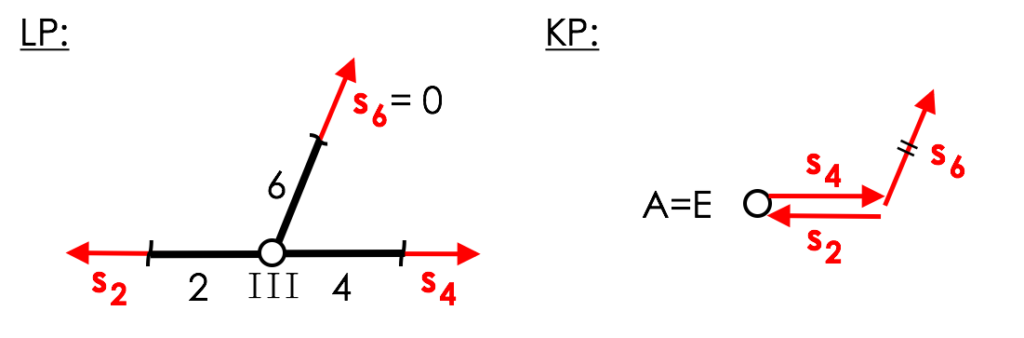
Video Nullstäbe beim Fachwerk erkennen
Ermittlung der Stabkräfte
Zunächst werden kurz die Besonderheiten der drei Verfahren zeichnerisches und rechnerisches Knotenpunktverfahren (vgl. Rolf Mahnken, Lehrbuch der Technischen Mechanik – Statik, Springer Verlag, 1. Auflage, 2012) sowie der Ritterschnitt dargestellt. Anschließend werden Lösungshinweise zu jedem Verfahren vorgestellt und in Beispielen angewendet.
Zeichnerisches Knotenpunktverfahren
- hier wird nichts gerechnet – nur abgelesen!
- Allgemein gilt: Es dürfen maximal 2 Unbekannte am Knoten angreifen
- Vorgehen: Rückblick zentrale ebene Kraftsysteme, wobei die Wirkungslinien beider Kräfte bekannt und die Beträge gesucht sind.
Lösungsschritte mit Beispiel:
Gegeben ist der Ausschnitt dieses Fachwerks und es sollen die Stabkräfte 1 und 2 mit dem zeicherischen Knotenpunktverfahren ermittelt werden.
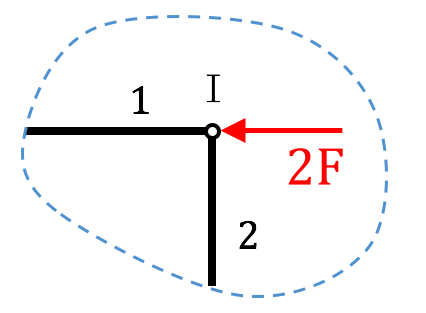
Dafür arbeiten wir einfach die folgenden Lösungsschritte ab.
(i) Lageplan: Eintragen aller bekannten Kräfte (Richtung bitte so, dass Zahlwert positiv ist) und Wirkungslinien der unbekannten Kräfte
(ii) Kräfteplan: Maßstäbliches Aneinanderreihen aller bekannten Kräfte. Anfangspunkt mit $A$ und vorläufiges Ende mit $E‘$ bezeichnen.
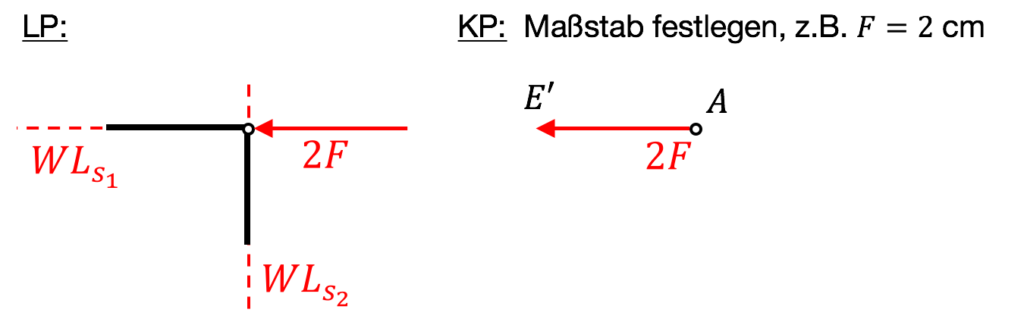
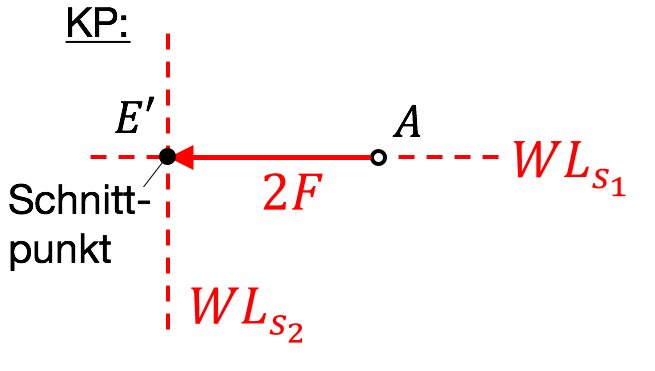
(iii) Bekannte Wirkungslinie in Kräfteplan: Eintragen der einen bekannten Wirkungslinie durch $A$, eintragen der anderen Wirkungslinie durch $E‘$ $\rightarrow$ Schnittpunkt suchen.
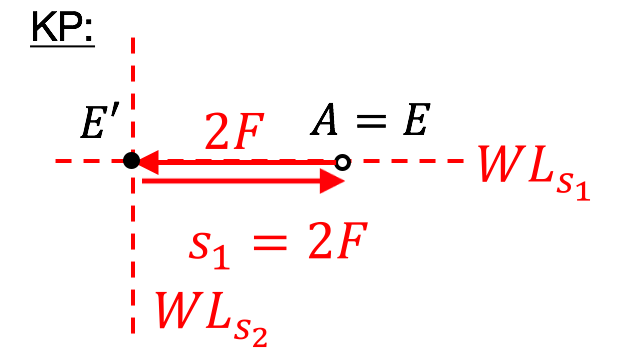
(iv) Schließen des Kräftepolygons: Es muss $A=E$ gelten, also Anfangspunkt gleich Endpunkt.
(v) Unbekannte Beträge entsprechend des Maßstabes aus Kräfteplan ablesen
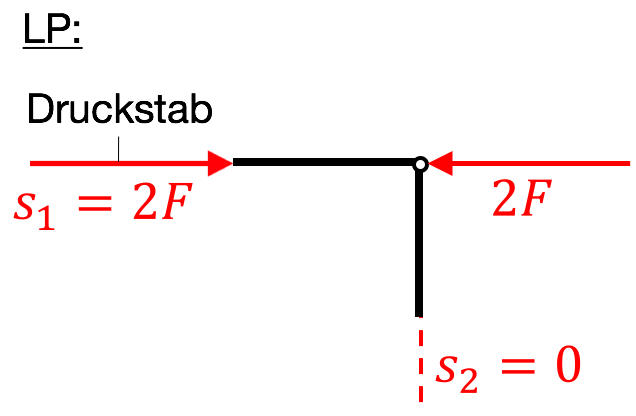
(vi) Übertragen der Kräfte nach Betrag und Richtung in Lageplan $\rightarrow$ angeben, ob es sich um einen Zug- oder Druckstab handelt!
Video Beispiel zeichnerisches Knotenpunktverfahren
Rechnerisches Knotenpunktverfahren
- Alle Stabkräfte werden im Lageplan direkt auf Zug angenommen
- Wenn Kraft negativ: Druckstab
- Wenn Kraft positiv: Zugstab
- Es sollten maximal 2 unbekannte Kräfte am Knoten angreifen
- Bestimmung der Unbekannten mittels Gleichgewicht am Knoten
- Summe der Kräfte in horizontaler Richtung
- Summe der Kräfte in vertikaler Richtung
Lösungsschritte mit Beispiel:
1. Knoten raussuchen, wo max. 2 Unbekannte Stabkräfte angreifen.

2. Lageplan zeichnen und unbekannte Stabkräfte immer auf Zug annehmen!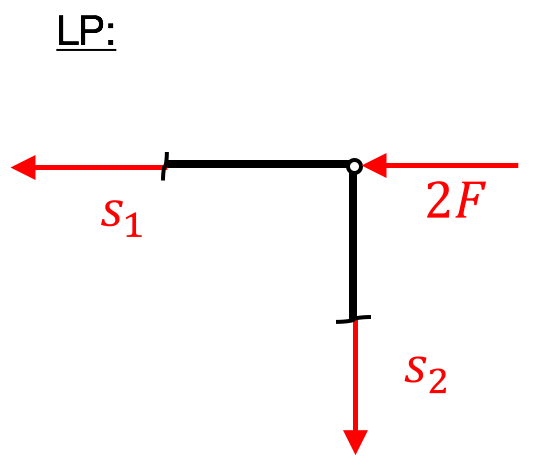
3. Gleichgewicht am Knoten bestimmen.
\begin{align*}
\leftarrow&: \ s_1+2F=0 \ \Leftrightarrow \ s_1=-2F \ \textrm{(Druckstab)} \\
\downarrow&: \ s_2=0
\end{align*}
Video Beispiel rechnerisches Knotenpunktverfahren
Ritterschnitt-Verfahren
- Praktisch, wenn nur einzelne Stabkräfte gesucht sind
- Vorgehen: Schnitt durch
- 3 nicht durch einen Knoten gehende Stäbe
- einen Stab und ein Gelenk
Anhand des folgenden Fachwerks soll der Ritterschnitt etwas näher erläutert werden. Wir haben zwei beliebige Ritterschnitte eingetragen und wollen nun die weitere Vorgehensweise durchspielen.
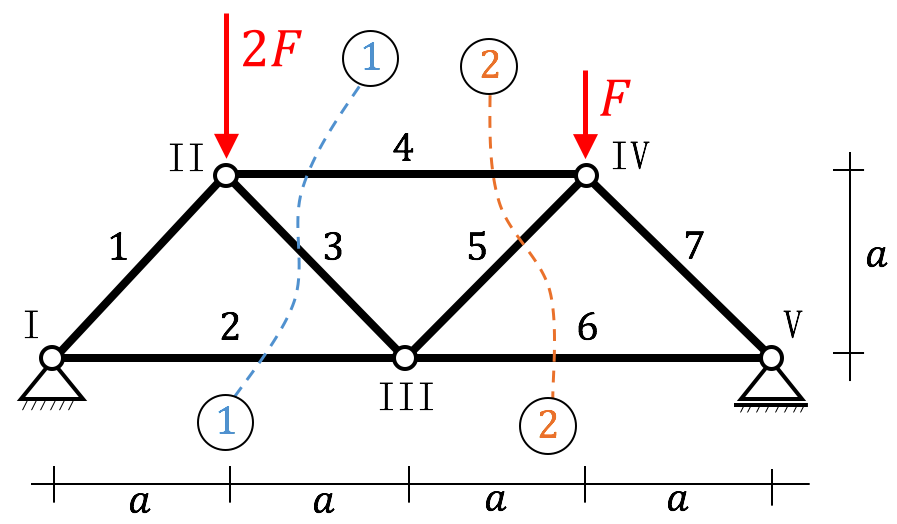
Betrachten wir den Schnitt 1. Durch den Ritterschnitt haben wir das Fachwerk in zwei Teile „geschnitten“, um die Stabkräfte sichtbar zu machen – Wichtig: Kräfte immer auf Zug annehmen! Ihr habt jetzt die Wahl, mit welcher Hälfte ihr weiterarbeiten wollt. Hier betrachten wir die linke Seite, weil es gefühlt weniger zu zeichnen ist. Wenn nun die Lagerreaktionen eingetragen werden, können die Stabkräfte $s_2, \ s_3$ und $s_4$ berechnet werden.
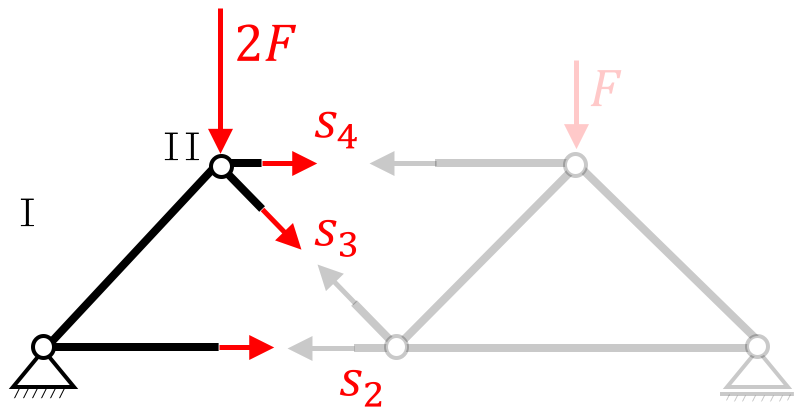
Die Lagerreaktionen im Lager $A$ lauten $A_x=0$ und $A_y = 7F/4$.
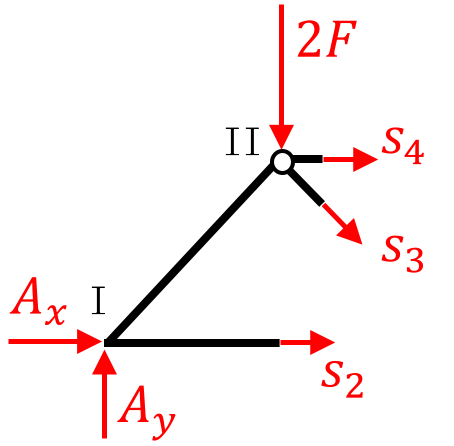
\begin{align*}
\unicode{8630} II&: \ s_2\cdot a + A_x\cdot a + A_y \cdot a=0 \quad \Leftrightarrow \quad s_2 = -A_y=-\frac{7}{4}F \ \textrm{(D)} \\
\unicode{8631} III&: \ s_4\cdot a -2F\cdot a + A_y \cdot 2a=0 \quad \Leftrightarrow \quad s_4 = 2F-2A_y=-\frac{3}{2}F \ \textrm{(D)} \\
\downarrow&: \ 2F-A_y + \frac{s_3}{\sqrt{2}}=0 \quad \Leftrightarrow \ \ s_3 = \sqrt{2}\cdot \left(\frac{7}{4}F-2F \right)=-\frac{1}{2\sqrt{2}}F \ \textrm{(D)}
\end{align*}
Da wir die Stabkräfte im Lageplan auf Zug angenommen haben, erhalten wir Druckstäbe (D) bzw. Zugstäbe (Z) wenn ein negatives bzw. positives Ergebnis rauskommt.
Video Beispiel Fachwerk Ritterschnittverfahren
Beispiele
Beispiel Fachwerk Klausuraufgabe
Gegeben ist das nebenstehende Fachwerk.
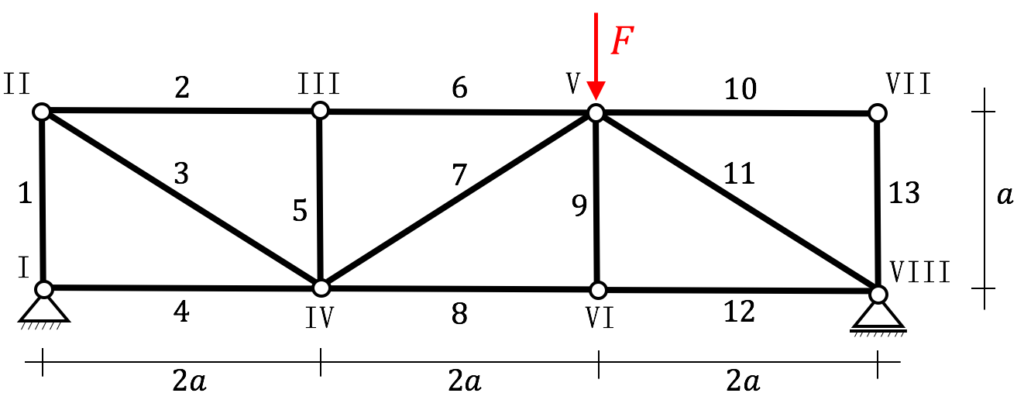
Folgende Aufgaben sind zu bearbeiten:
1) Prüfung auf statische Bestimmtheit.
Notwendige Bedingung: $f=2k-(r+s)=2\cdot 8-(3+13)=0 \ \unicode{10003}$
Hinreichende Bedingung: 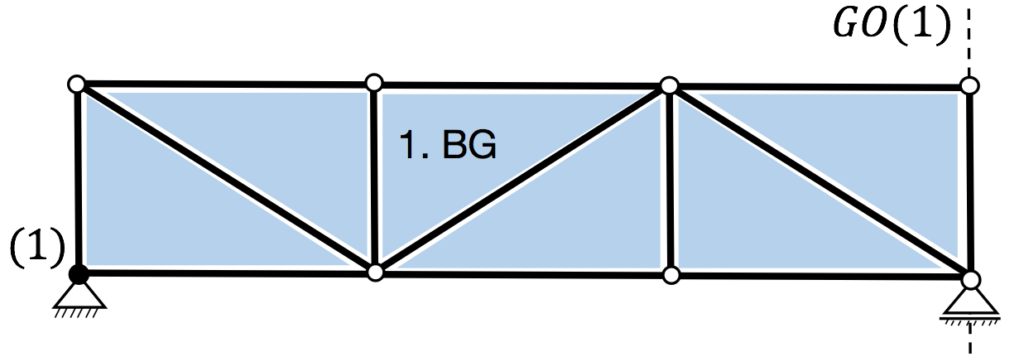
1. Bildungsgesetz: innerlich statisch bestimmt.
Polplan liefert einen Widerspruch (geom. Ort schneidet nicht Pol) und aus diesem Grund ist das Fachwerk statisch bestimmt.
2) Berechne die Lagerreaktionen.
Hier sollte zunächst ein Freischnitt gemacht werden. Es ist nicht notwendig, das Fachwerk mit allen inneren Stäben erneut abzumalen! 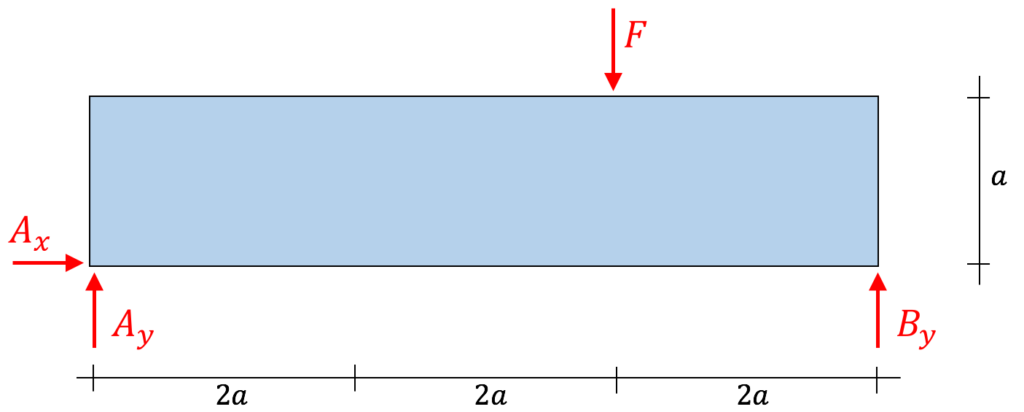
Gleichgewichtsbedingungen:
\begin{align*}
\rightarrow&: \ A_x=0 \\
\unicode{8630} A&: \ B_y\cdot 6a – F\cdot 4a=0 \ \Leftrightarrow \ B_y = \frac{2}{3}F \\
\uparrow&: \ A_y-F+B_y=0 \ \Leftrightarrow \ A_y=\frac{1}{3}F
\end{align*}
3) Nenne die Nullstäbe.
Regel 1: $s_{10}$ und $s_{13}$
Regel 2: keiner
Regel 3: $s_5$ und $s_9$
4) Bestimme die Stabkräfte $s_1$ und $s_4$ mit dem rechnerischen Knotenpunktverfahren. Gib dabei an, ob es sich um einen Zug- oder Druckstab handelt.
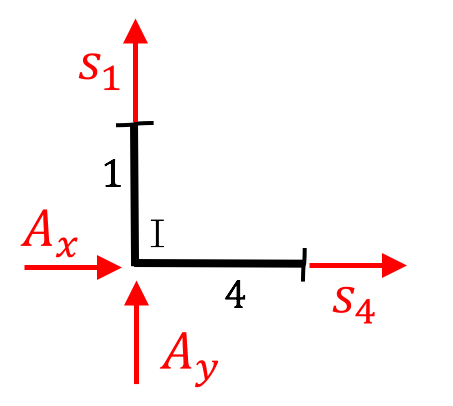
\begin{align*}
\rightarrow: \ s_4+A_x=0 \ &\Leftrightarrow \ s_4=-A_x=0 \\
\uparrow: \ s_1+A_y=0 \ &\Leftrightarrow \ s_1=-A_y=-\frac{1}{3}F \ \textrm{(D)}
\end{align*}
Wir haben den Knoten freigeschnitten und die unbekannten Stabkräfte auf Zug im Lageplan eingetragen. Über das Kräftegleichgewicht am Knoten erhalten wir die gesuchten Größen.
5) Bestimme die Stabkraft $s_6$ mit dem Ritterschnitt.
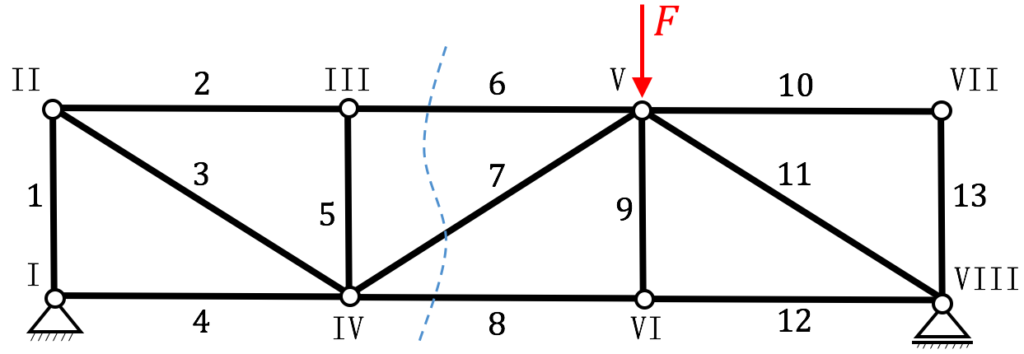
Um die gesuchte Stabkraft zu ermitteln, müssen wir das Fachwerk gemäß den Vorgaben schneiden. Den Schnitt legen wir durch Stab 6, 7, und 8, um schnell zum Ergebnis zu kommen. Im Lageplan nehmen wir die Stabkräfte wie immer auf Zug an.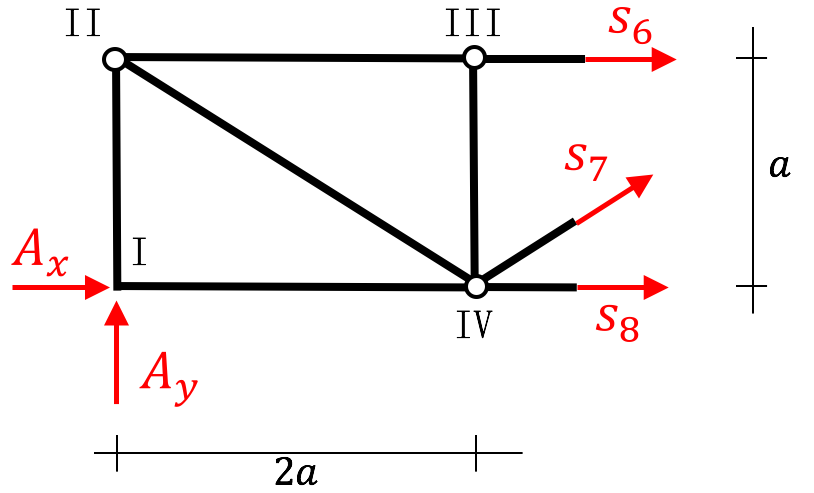
\begin{align*}
\unicode{8631} IV: \ s_6\cdot a + A_y \cdot 2a=0 \quad \Leftrightarrow \ s_6 = -2A_y=- \frac{2}{3}F \ \textrm{(D)}
\end{align*}
Lösungsvideo zum Beispiel

19,99€

