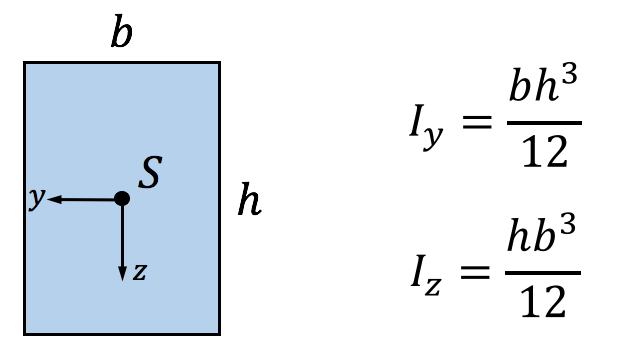Flächenträgheitsmomente
- Auch Flächenmoment 2. Ordnung genannt
- SI-Einheit: m$^4$
- Abhängig vom Querschnitt
- Gibt Widerstand des Körpers gegen Biegung an
- Praktische Berechnung zusammengesetzter Querschnitte mit dem Tabellenverfahren
- Flächenträgheitsmomente beziehen sich hier zunächst auf die Schwerachsen (kleine Buchstaben im Index – bei Hauptachsen sind große Buchstaben) $I_y$, $I_z$, $I_{yz}$
Die Flächenträgheitsmomente einer beliebigen Querschnittsfläche werden mit Hilfe des Satzes von Steiner berechnet. Der Satz von Steiner besagt, dass sich das Flächentragheitsmoment aus dem Flächenträgheitsmoment in den Flächenmittelpunkten der einzelnen Teilflächen und dem Produkt aus dem Quadrat des Abstandes $z$ von Schwerachse-Gesamtfläche zu Schwerachse-Teilfläche und Teilfläche $A$ zusammensetzt.[3]
[3] https://de.wikipedia.org/wiki/Flächenträgheitsmoment
Es gilt:
\begin{align*}
I_y &= \sum I_{y_i} + \sum z_i^2 \cdot A_i \\
I_z &= \sum I_{z_i} + \sum y_i^2 \cdot A_i \\
I_{yz} &= \sum I_{yz_i} – \sum y_i \cdot z_i \cdot A_i \
\end{align*}

19,99€
Praktische Berechnung mit Tabellenverfahren
Wie bei der Berechnung des Flächenschwerpunktes, bietet sich die Verwendung einer Tabelle an. Betrachten wir dazu das Beispiel aus dem Kapitel Schwerpunkt berechnen mit den Schwerpunktkoordinaten $\bar{y}_s = 50,71$ cm und $\bar{z}_s = 37,14$ cm.
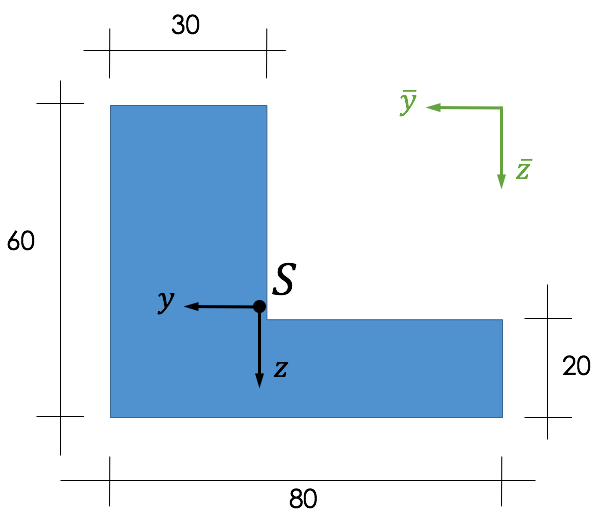
Hier die ausgefüllte Tabelle für unser Beispiel:
Für die einzelnen Flächenträgheitsmomente einfacher Teilflächen wie Dreiecken, Rechtecken, Kreisen etc. empfiehlt sich ein Blick in eines der zahlreichen Tabellenbücher. Z.B. gilt für ein Rechteck:
Die Flächenträgheitsmomente lauten für dieses Beispiel:
\begin{align*}
I_y &= 573333,33 + 257142,88 = 830476,21 \ \textrm{cm}^4 \\
I_z &= 343333,33 + 1028571,48 = 1371904,81 \ \textrm{cm}^4 \\
I_{yz} &= 0 – (-514285,68) = 514285,68 \ \textrm{cm}^4
\end{align*}
Video Flächenträgheitsmomente mit Tabellenverfahren berechnen
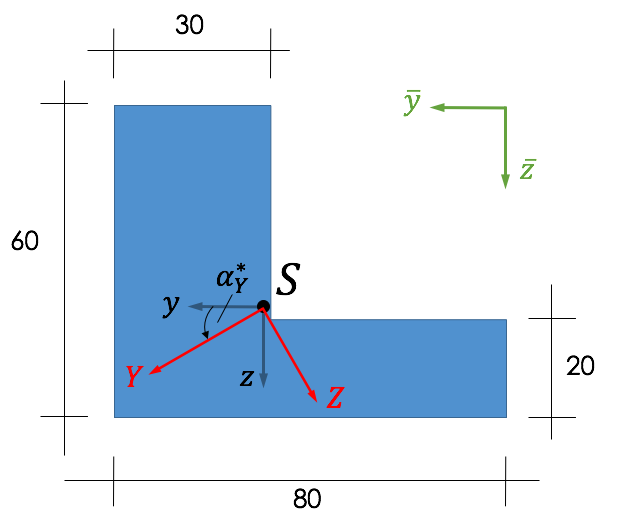
Hauptachsen & Hauptträgheitsmomente
- Schwerachsen werden so gedreht, dass Flächenträgheitsmomente maximal ($I_Y$) bzw. minimal ($I_Z$) werden
- Vorteil: In den Hauptträgheitsachsen (kurz: Hauptachsen) verschwindet das Deviationsmoment $I_{YZ}=0$
- Beachte die Schreibweise: Indizes werden bei Hauptträgheitsmomenten groß geschrieben!
Formeln zur Berechnung der Hauptträgheitsmomente:
\begin{align*}
I_Y &= I_{max} = \frac{I_y + I_z}{2} + \sqrt{ \left( \frac{I_y – I_z}{2} \right)^2 + I_{yz}^2} \\
I_Z &= I_{min} = \frac{I_y + I_z}{2} – \sqrt{ \left( \frac{I_y – I_z}{2} \right)^2 + I_{yz}^2} \\
I_{YZ} &= 0
\end{align*}
Für unser Beispiel lauten die Hauptträgheitsmomente:
\begin{align*}
I_Y &= 1682375,5 \ \textrm{cm}^4 \\
I_Z &=520005,52 \ \textrm{cm}^4 \\
I_{YZ} &= 0
\end{align*}
Formel zur Berechnung des Winkels der Hauptachsen:
\begin{align*}
\tan \alpha_Y^* = \frac{I_{yz}}{I_Y – I_Z} \quad \textrm{und} \quad \alpha_Z^* = \alpha_Y^* + \frac{\pi}{2}
\end{align*}
Beachte: In der Mechanik ist der positive Drehsinn entgegen dem Uhrzeigersinn.
Für dieses Beispiel lauten die Winkel der Hauptachsen:
\begin{align*}
\alpha_Y^* = 23,87^\circ \quad \textrm{und} \quad \alpha_Z^* = 113,87^\circ
\end{align*}
In dem folgenden Bild sind die Hauptachsen $Y-Z$ eingetragen, die um den Winkel $\alpha_Y^*$ um das Schwerachsensystem gedreht wurden. Vorteil: Im Hauptachsensystem verschwindet das Deviationsmoment $I_{YZ}$.