Prinzip der virtuellen Arbeit
In diesem Artikel erklären wir dir alles zum Thema „Prinzip der virtuellen Arbeit“. Wir gehen dabei auf folgende Themen ein:
19,99€
Definition
Häufig wird in den Übungen das Prinzip der virtuellen Arbeit (kurz: P.d.v.A.) zur Berechnung von Lagerreaktionen verwendet.
Grundgedanke: Kräfte führen virtuelle (gedachte) Bewegung durch!
- In Wirklichkeit nicht vorhanden
- Infinitesimal klein (Tangentenregel)
- Geometrisch zulässig
Merke: „Jede Bewegung eines starren Körpers ist als Drehung um einen Absolutpol (M) darstellbar. Dieser kann auch im Unendlichen liegen.“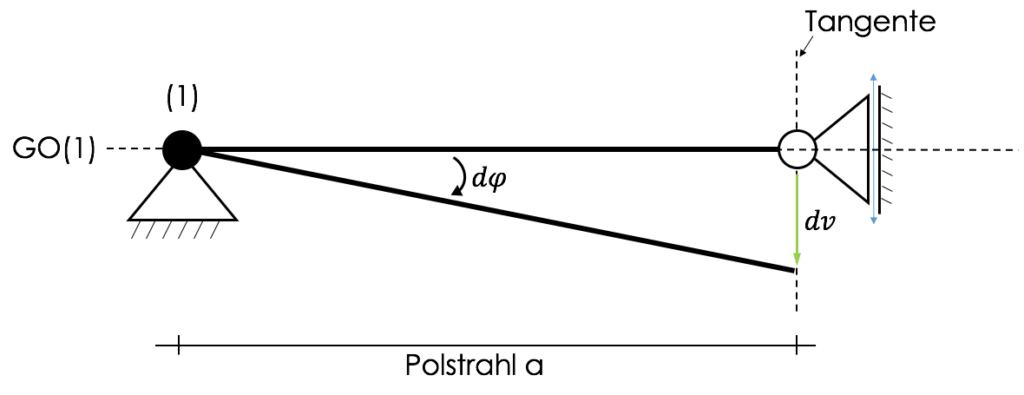
Der Zusammenhang zwischen Verdrehung $d\varphi$ und Verschiebung $dv$ kann mit dem Tangens ausgedrückt werden:
\begin{align*} \tan(d\varphi)=\frac{dv}{a} \end{align*}
Für kleine Winkel gilt $\tan(d\varphi)=d\varphi$ und somit vereinfacht sich der Ausdruck zu:
\begin{align*} d\varphi=\frac{dv}{a} \end{align*}
Fahrplan zur Berechnung von Lagerraktionen
Vorgehen: (vgl. Rolf Mahnken, Lehrbuch der Technischen Mechanik – Statik, Springer Verlag, 1. Auflage, 2012)
1) Lösen der Bindung: System ist dann verschiebbar ($f=1$)
Hinweis: Wenn das Schnittmoment an einer bestimmten Stelle bestimmt werden soll, muss ein Gelenk eingeführt werden. Das Moment tritt stets paarweise auf, weshalb du 2 Momente entgegengesetzt eintragen musst. Das ist dann die gesuchte Unbekannte.
2) Polplan erstellen (siehe Regeln Polplan)
3) Verschiebungsfigur zeichnen
4) PdvA aufstellen: $\delta A= \sum F_i \cdot \delta a_i + \sum M_i \cdot \delta \varphi = 0$
Tipp: in Abhängigkeit einer unabhängigen kinematischen Größe – also entweder vom Winkel oder einer bestimmten Länge. Wichtig bei mehrteiligen Systemen: Zusammenhang zwischen den verschiedenen Winkeln!
5) Auflösen nach unbekannter Größe
Beispiele
Beispiel mehrteiliges System
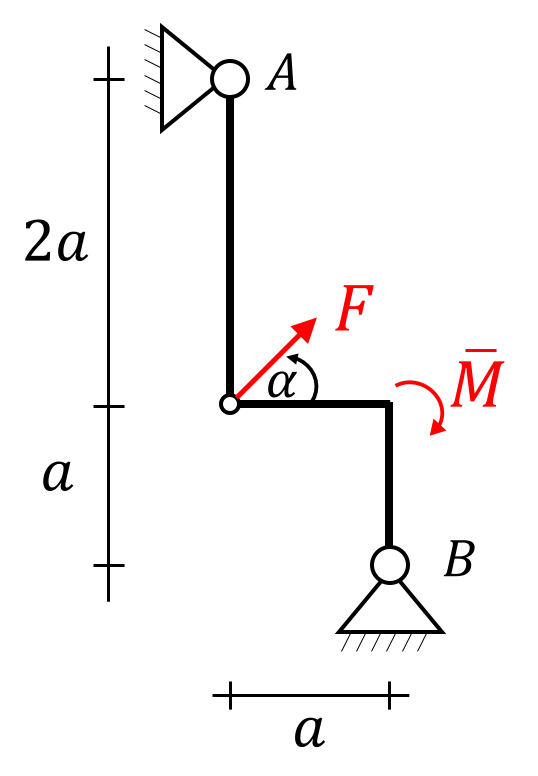
Bestimme die vertikale Auflagerreaktion des unteren Lagers B mit Hilfe des Prinzips der virtuellen Arbeit. Bekannt: $F, \ \overline{M}=F \cdot a, \ a, \ \alpha=45^{\circ}$
Lösung:
Wir arbeiten einfach den Fahrplan zur Berechnung von Lagerreaktionen ab, um die Lösung zu erhalten.
1. Bindung lösen – Was heißt das?
Gesucht ist die vertikale Lagerreaktion . Um diese zu bestimmen, machen wir aus dem Festlager ein Loslager und tragen die gesuchte Kraft ein.
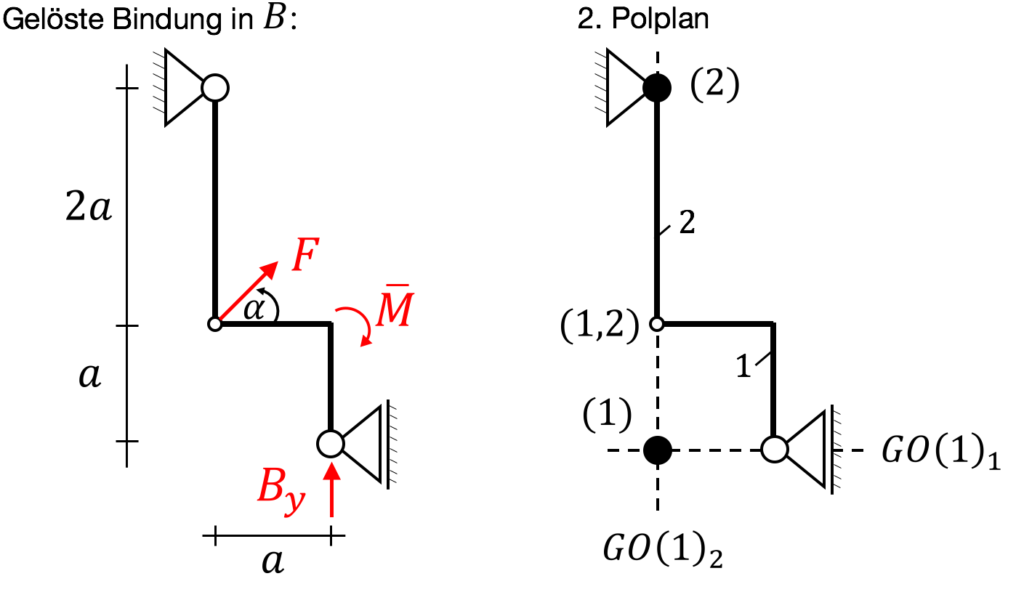
Für den Polplan müssen wir etwas improvisieren. Jedes System muss einen Pol haben. Bei System 2 ist sofort durch das Festlager klar, wo der Pol ist. Bei System 1 ist es etwas kniffliger. Zunächst kann der geometrische Ort beim Loslager eingetragen werden. Dann bedient man sich der Regel 5, um ein verschiebbares System zu erschaffen. Dazu erzeugen wir einen zusätzlichen geometrischen Ort, der Pol (2) und den Zwischenpol verbindet. Dies ist ein geometrischer Ort von System 1! Der Schnittpunkt der beiden geometrischen Orte ergibt den Pol von System 1. Das System ist nun verschiebbar.
3. Verschiebungsfigur ausgehend vom Polplan zeichnen
Bei mehrteiligen Systemen sollte immer der Zusammenhang zwischen den verschiedenen Verdrehwinkeln $\delta \varphi_i$ hergestellt werden.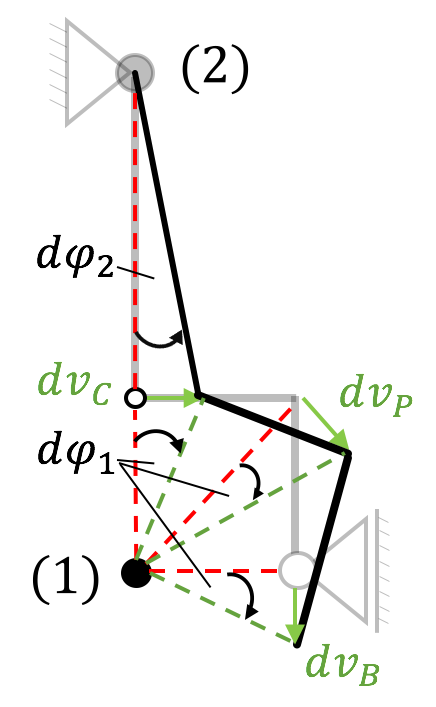 
Dazu schauen wir uns den Zwischenpol an, der von beiden Polen aus verschoben werden kann. Es gilt:
\begin{align*}
d\varphi_2\cdot 2a &= dv_C= d \varphi_1 \cdot a \\
\Rightarrow \ d\varphi_1 &= 2\varphi_2
\end{align*}
4. P.d.v.A. aufstellen
Hier muss nun beachtet werden, ob die angreifenden äußeren Kräfte mit der virtuell gedachten Verschiebung oder dagegen wirken. Daraus resultiert dann das Vorzeichen.
\begin{align*}
dA = \sum F_i \cdot da_i + \sum M_i \cdot d \varphi
\end{align*}
Aus obiger Gleichung folgt:
\begin{align*}
dA= -B_y \cdot dv_B + F\cdot \cos(\alpha) \cdot dv_C+\overline{M}\cdot d\varphi_1 =0
\end{align*}
5. Im Gleichgewicht muss dieser Ausdruck gleich Null sein. Nun die Gleichung in Abhängigkeit von nur einer virtuellen Größe umstellen und diese Ausklammern.
\begin{align*}
-B_y \cdot d\varphi_1 \cdot a + F\cdot \cos(\alpha) \cdot d\varphi_1 \cdot a +\overline{M}\cdot d\varphi_1 &=0 \\
d\varphi_1 \cdot \left( -B_y \cdot a + F\cdot \cos(\alpha) \cdot a +\overline{M} \right) &=0
\end{align*}
Wie lösen wir diesen Ausdruck? Merke: Ein Produkt ist dann Null, wenn einer der beiden Faktoren Null ist. Da virtuelle Größen beliebig, aber in der Regel ungleich Null sind, muss der Klammerausdruck gleich Null sein. Es folgt das Ergebnis:
\begin{align*}
B_y = F\cdot \cos(\alpha) +\frac{\overline{M}}{a} = F\cdot \frac{1}{\sqrt{2}} + \frac{F\cdot a}{a}=\frac{F}{\sqrt{2}} +F
\end{align*}
Video zur Beispielaufgabe – Berechnung der Lagerkraft $A_y$
19,99€
Aufgabe Schnittmoment einteiliges System
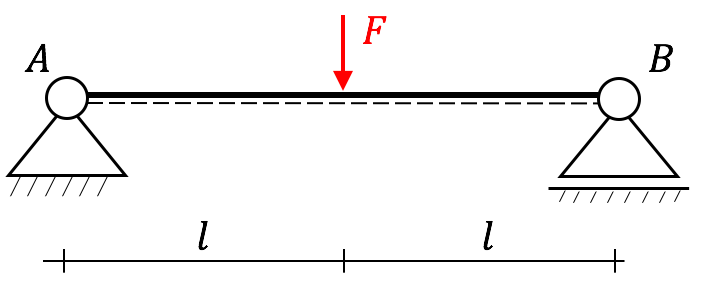
Bestimme mit Hilfe des P.d.v.A. das Schnittmoment in Balkenmitte. Bekannt: $\overline{M}, \ l$
Lösungsvideo zur Aufgabe:
