
Reibung
Im folgenden Artikel findest du Erklärungen, Aufgaben und Videos zum Thema Reibung. Dabei behandeln wir sowohl die verschiedenen Zustände als auch das Thema Seilreibung:

19,99€
Definition
Reibung ist ein Widerstand in den Kontaktflächen von zwei Körpern, der eine gegenseitige Bewegung durch Gleiten, Rollen oder Abwälzen verhindert oder zumindest beeinträchtigt.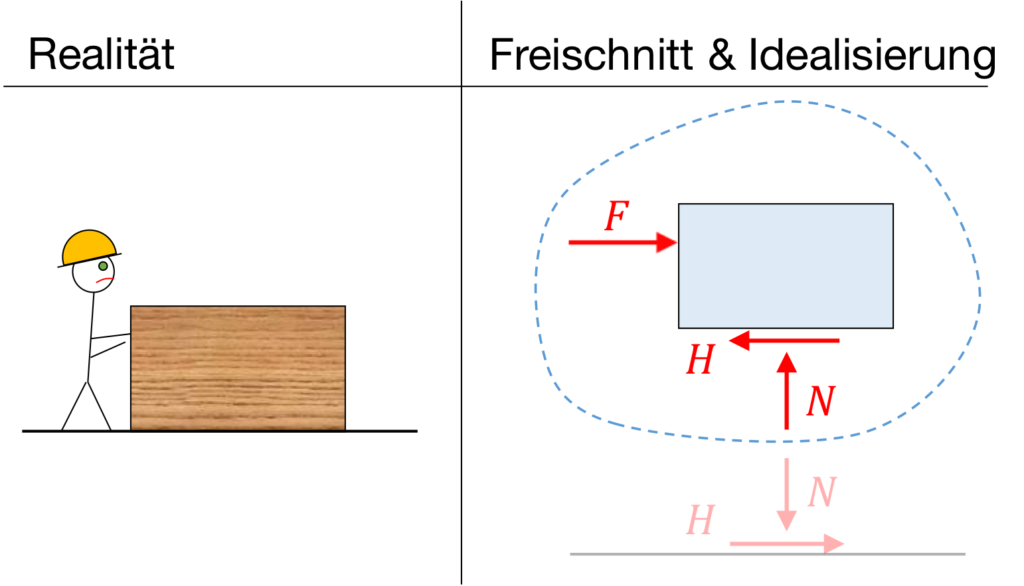
Wenn in der „Realität“ ein Bauarbeiter versucht eine Kiste wegzuschieben, wirkt die Reibungskraft $H$ dagegen, wie man im Freischnitt sehen kann. Zudem wirkt eine Normalkraft $N$.
Ob die Kiste nun rutscht, hängt von der Beschaffenheit der Kiste, des Untergrunds sowie der ausgeübten Kraft $F$ ab.
Wir unterscheiden bei der Reibung 4 verschiedene Zustände (vgl. Rolf Mahnken, Lehrbuch der Technischen Mechanik – Statik, Springer Verlag, 1. Auflage, 2012):
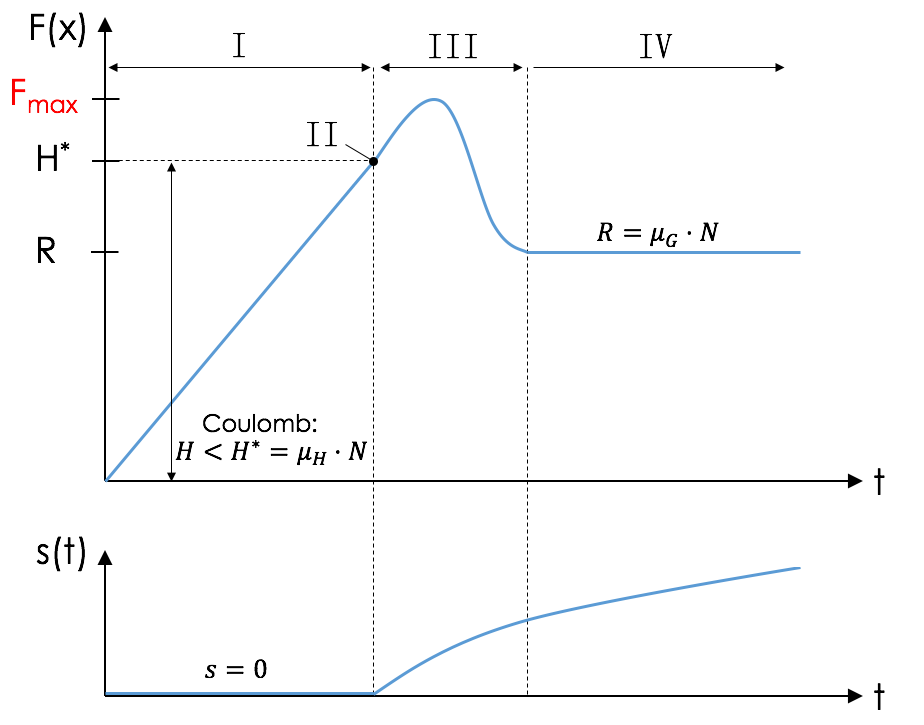
I – Haftreibungszustand
Der Haftreibungszustand beschreibt den Ruhestand, bei dem alle am Körper wirkenden Kräfte im Gleichgewicht sind.
II – Grenzzustand
Im Grenzzustand erreicht die Reibungskraft $H$ den Grenzhaftreibungskraft $H^*$.
III – Beschleunigungszustand
In diesem Zustand wird der Körper kurzzeitig beschleunigt.
IV – Gleitreibungszustand
Hier befindet sich der Körper in gleichförmiger Bewegung mit konstanter Geschwindigkeit im Gleichgewicht. Anstatt der Reibungskraft $H$ wirkt die Kontaktkraft $R^*$.
Wichtig für uns:
Zustand I und II gehören zur Statik (dieses Ebook)
Zustand III und IV gehören zur Dynamik!
Bei Aufgaben zum Thema Reibung in der Statik muss der Aufgabentext genau gelesen werden! Sobald Angaben wie „maximal“, „minimal“, „höchstens“ etc. dort stehen, befindet man sich in Zustand II und man muss mit dem Haftreibungsgesetz nach Coulomb arbeiten. Es gilt:
\begin{align*}
H^*=\mu_H \cdot N
\end{align*}
mit $\mu_H$ als Haftreibungskoeffizient, welcher abhängig ist von der
- Werkstoffpaarung
- Geometrischer, physikalischer Oberfläche
- Temperatur
und $N$ als Normalkraft.
Beispiel
Eine Kiste mit der Masse $m$ liegt auf einer schiefen Ebene, siehe Abbildung.
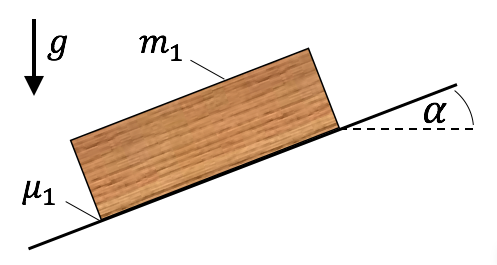
a) Bestimme die Reaktionskräfte in der Kontaktfläche.
b) Wie groß muss $\alpha^*$ sein, damit gerade kein Rutschen auftritt? Wie groß sind dann die Reaktionskräfte?
Bekannt: $\alpha = 30^o, \ m=10 \ \textrm{kg}, \mu_1=0,6, \ g=10 \ \textrm{m/s}^2$
Lösungsschritte zu a)
1. Freischnitt zeichnen: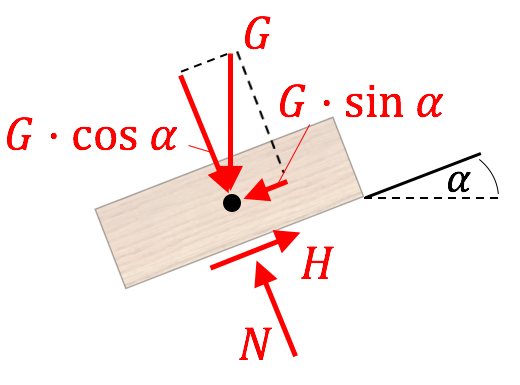
2. Berechnung der Reaktionskräfte:
Die Unbekannten lauten $N$ und $H$. Dafür stellen wir einfach zwei Gleichgewichtsbedingungen auf.
\begin{align*}
\searrow: \ G \cdot \cos \alpha -N=0 \ &\Leftrightarrow \ N=G \cdot \cos \alpha = 86,6 \ \textrm{N} \\
\nearrow: \ H – G \cdot \sin \alpha =0 \ &\Leftrightarrow \ H=G \cdot \sin \alpha = 50 \ \textrm{N}
\end{align*}
Für die maximale Haftreibungskraft gilt nach dem Haftreibungsgesetz (Coulumb):
\begin{align*}
H^* = \mu_1 \cdot N =0,6 \cdot 86,6\ \textrm{N} = 51,96\ \textrm{N} > 50\ \textrm{N} = H
\end{align*}
Da der Grenzzustand $H^*$ größer ist als die auftretende Haftreibung $H$ bleibt die Kiste in Ruhe.
Lösungsschritte zu b)
Wir verwenden den Freischnitt aus a) – aber hier befinden wir uns im Grenzzustand! Dieser Hinweis ist im Text gegeben: „gerade kein Rutschen“. Aus diesem Grund tragen wir im Freischnitt nun die Unbekannten $N^*$, $H^*$ und $\alpha^*$ ein.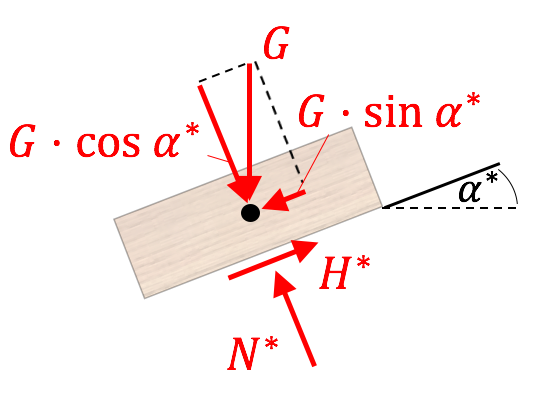
Da wir uns im Grenzzustand befinden, können wir das Haftreibungsgesetz verwenden. Das brauchen wir als zusätzliche dritte Gleichung, um die drei Unbekannten zu bestimmen. Dazu setzen wir die Gleichgewichtsbedingungen
\begin{align*}
H^*=G \cdot \sin \alpha^* \quad \textrm{und} \quad N^*=G \cdot \cos \alpha^*
\end{align*}
in das Haftreibungsgesetz $ H^* = \mu_1 \cdot N^* $ ein:
\begin{align*}
G\cdot \sin \alpha^* = \mu_1 \cdot G\cdot \cos\alpha^* \ \Leftrightarrow \ \frac{\sin \alpha^*}{\cos \alpha^*}=\mu_1 \ \Rightarrow \tan \alpha^* = \mu_1
\end{align*}
Daraus folgt für den Winkel: $ \alpha^* = \arctan\mu_1 = 30,96^o > \alpha$.
Die Reaktionskräfte lauten:
\begin{align*}
H^*=G \cdot \sin \alpha^* = 51,44 \ \textrm{N} \quad \textrm{und} \quad N^*=G \cdot \cos \alpha^* = 85,75 \ \textrm{N}
\end{align*}
Video einfaches Beispiel Reibung

19,99€
Seilreibung
Seilreibung tritt auf, wenn ein Seil über eine gewölbte Fläche (z.B. ein Zylinder) gelegt wird und an beiden Enden durch zwei Kräfte belastet wird.
Im Grenzzustand können wir den Zusammenhang der Seilkräfte über die Seilreibungsformel nach Euler und Eytelwein aufstellen.
Hierbei muss zunächst geklärt werden, welche Seite die Lastseite ist.
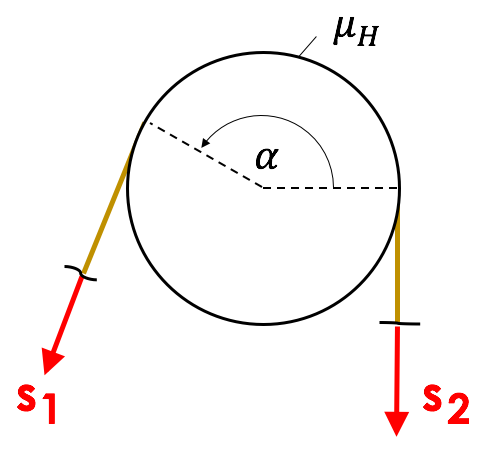
Wenn $s_2>s_1$, dann gilt:
\begin{align*}
s_2 = s_1 \cdot e^{\mu \cdot \alpha}
\end{align*}
mit $\alpha$ als Umschlingungswinkel – dieser muss im Bogenmaß angegeben werden!
Hinweis zur Umrechnung vom Winkel zum Bogenmaß:
Winkel in Grad mit $\frac{\pi}{180^o}$ multiplizieren, z.B. sind 360° im Bogenmaß $360 \cdot \frac{\pi}{180^o} = 2 \pi$.
Beispiel Haft- und Seilreibung in Kombination
Gegeben sei das nachfolgende System. In dieser Aufgabe tritt neben der Haftreibung an der Kiste auch Seilreibung auf.
Wie schwer muss die Kiste mit der Masse $m_2$ sein, damit die Kiste mit der Masse $m_1$ gerade nicht nach
a) oben und
b) unten rutscht?
Bekannt: $m_1=50 \ \textrm{kg}, \ m_2=0,5 m_1, \ \alpha=20^o, \ \beta =\gamma =30^o,$ $\mu_1=0,6,\ \mu_2=\mu_3=0,2, \ g = 10 \ \textrm{m/s}^2$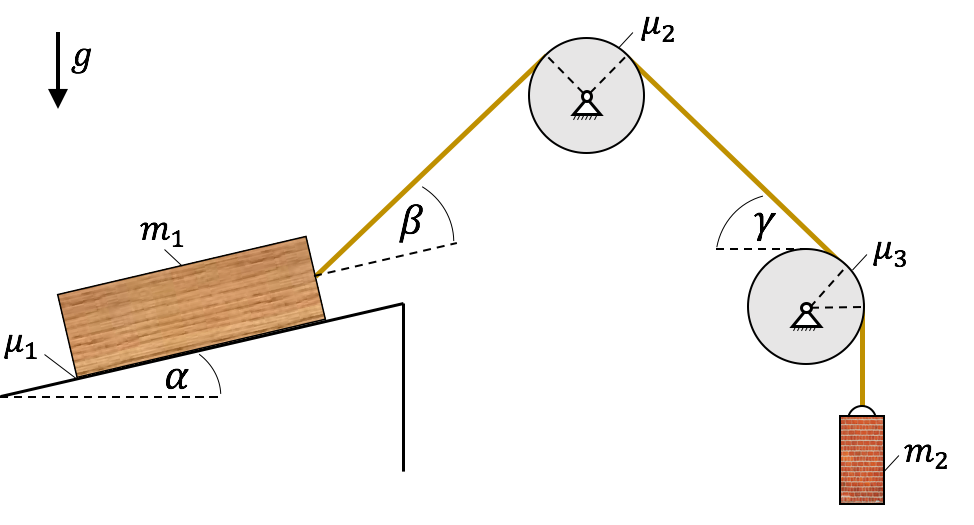
Video – ähnliches Beispiel Haft- und Seilreibung

19,99€
