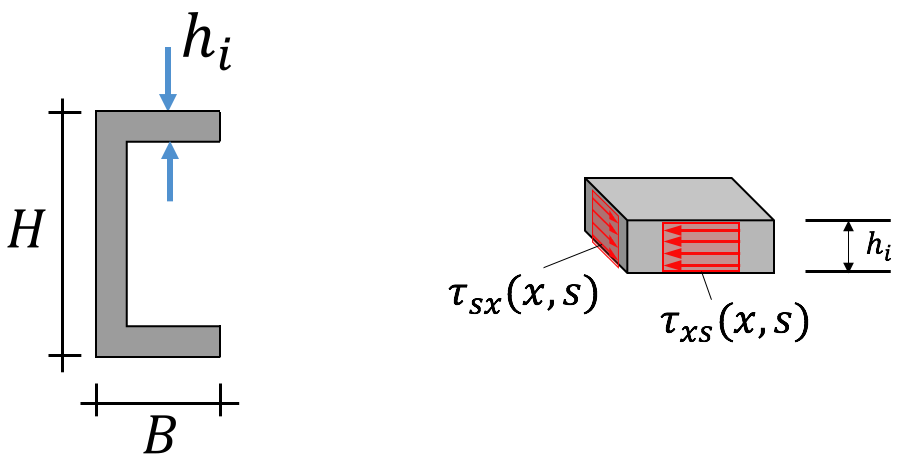
Schubspannung infolge Querkraft
Voraussetzungen
- Wanddicken $h_i$ klein gegenüber Höhe $H$ und Breite $B$
- Querschnitt in Richtung der Balkenachse konstant
- $y-z$-Achsen gehen durch Schwerpunkt und sind Hauptachsen
- jede freie Oberfläche ist Lastfrei
19,99€
Hypothesen
- Schubspannungen sind randparallel
- Schubspannungen über Dicke konstant
Formeln:
\begin{align*}
&\textrm{Schubspannung:} \ \tau_{xs}(x,s) = \frac{t(x,s)}{h(s)} \\
&\textrm{mit} \ t(x,s) = -\frac{Q_z(x) \cdot S_y (s)}{I_y} \quad \textrm{als Schubfluss} \\
&\textrm{und} \ S_y(x,s) = \int_{s_0}^s z(\tilde{s}) \cdot h(\tilde{s}) d\tilde{s} \quad \textrm{als Statisches Moment.} \\
\end{align*}
Eigenschaften
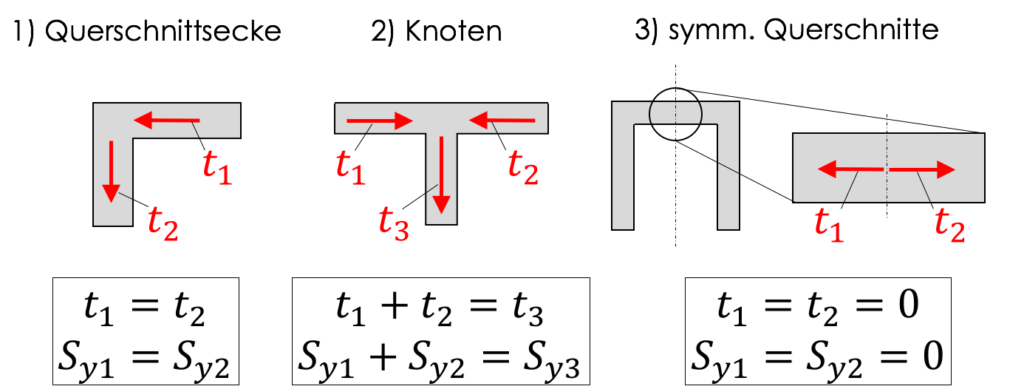
Querschnittskoordinate s:
- kann beliebig gewählt werden!
- zweckmäßig so, dass die dem zu erwartendem Schubfluss entspricht. Beginn also da, wo $t=0$ ist! Beispiele:
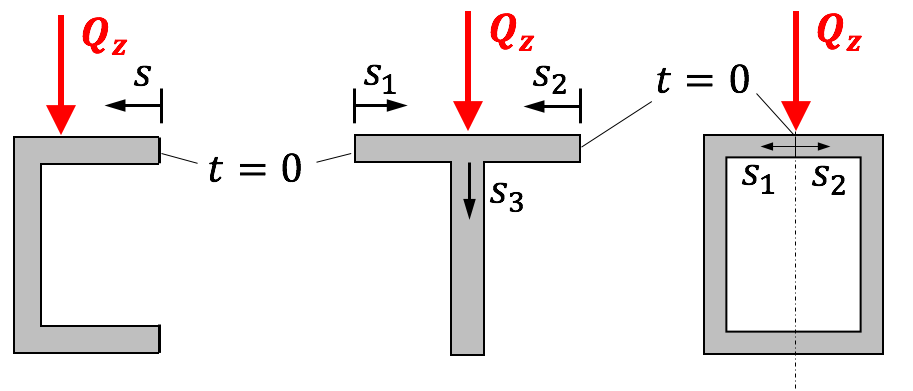
Praktische Berechnung mittels dem grafo-analytischem Verfahren „z*h-Linie“
1. Querschnittskoordinate bei $t=0$ einführen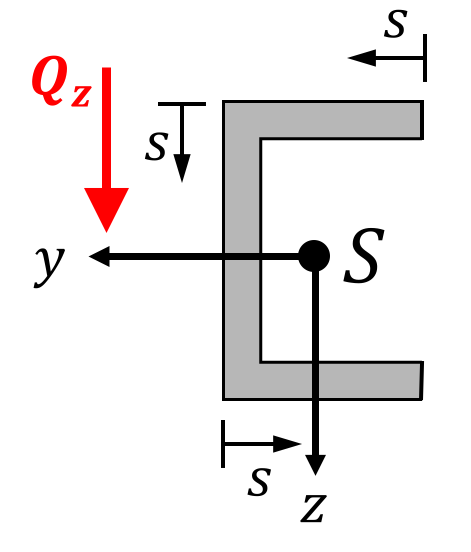
2. $z \cdot h(s)$-Linie [mm$^2$]
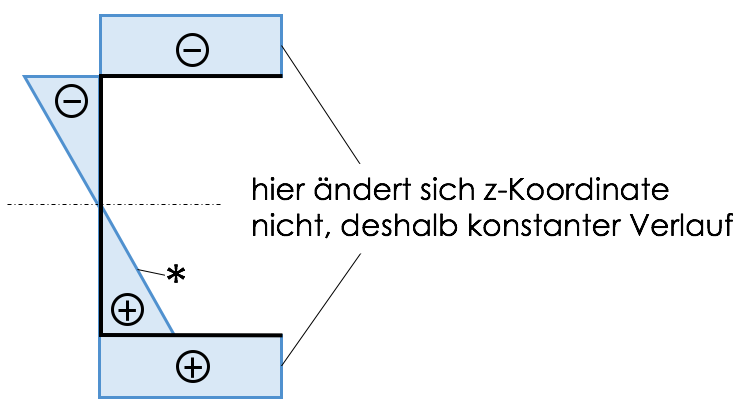mit $z$ als Abstand vom Schwerpunkt und $h(s)$ als Dicke des Querschnitts
3. Statisches Moment = Flächeninhalt der $z \cdot h(s)$-Linie [mm$^3$]
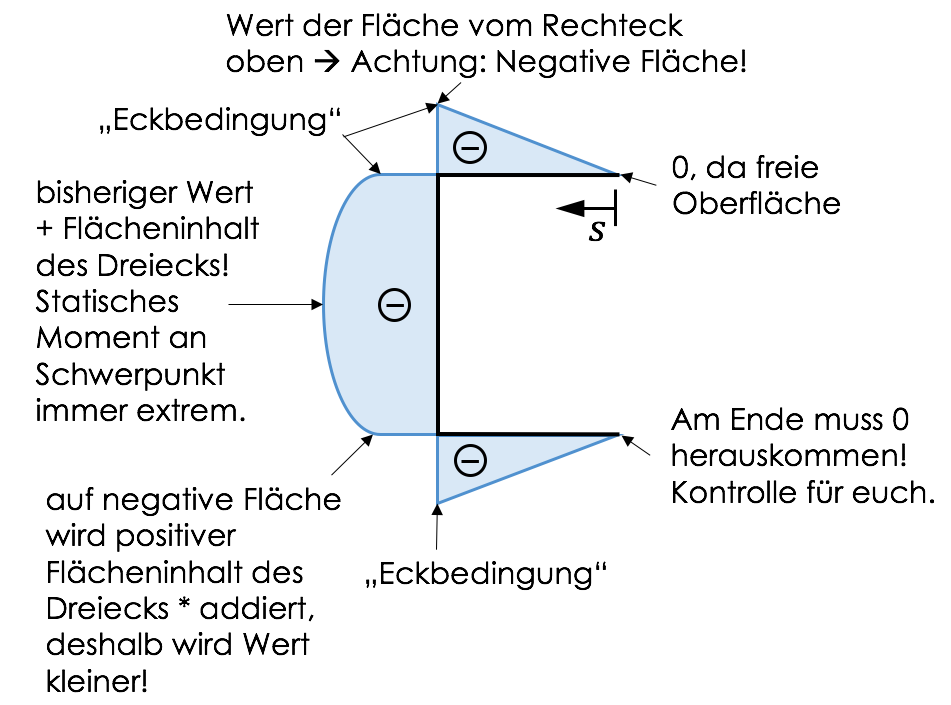
4. Schubfluss $t(s) = -\frac{Q_z \cdot S_y (s)}{I_y}$ [N/mm]
Achtung: Vorzeichen dreht um!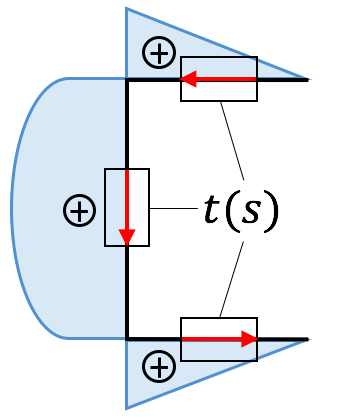
5. Schubspannung $\tau_{xs}(s) = \frac{t(s)}{h(s)}$ [N/mm$^2$]
Hinweis: Falls der Schubfluss oder die Schubspannungen vom Verlauf her eingetragen werden sollen:
(i) Schubfluss 1 Pfeil
(ii) Schubfluss 3 Pfeile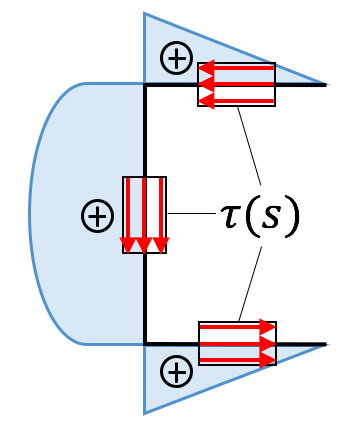
Video Schubspannung in Folge einer Querkraftbelastung mit z*h-Linie
Video Verlauf der Schubspannung an unterschiedlichen Profilen
Neu!