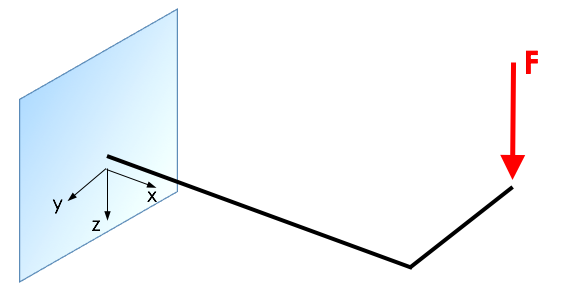
Die Technische Torsionstheorie
$\rightarrow$ Belastung $F$ führt zu einem Torsionsmoment $M_T(x)$ und folglich zu einer Verdrehung $\vartheta$ des eingespannten Trägers.

19,99€
Einteilung der Torsion
Merkmal Belastung:
- Reine Torsion $\rightarrow$ bei Schnittgrößen nur $M_T(x)=0$
- Torsion mit Streckenlast $\rightarrow$ $M_T(x) \neq 0$
Merkmal Theorie zur Verwölbung:
- Torsion ohne Wölbbehinderung (St. Venant) $\rightarrow$ $u_x(x)\neq 0; \ \sigma_x=0$
- Torsion mit Wölbbehinderung $\rightarrow$ $u_x(x) =0; \ \sigma_x \neq 0$
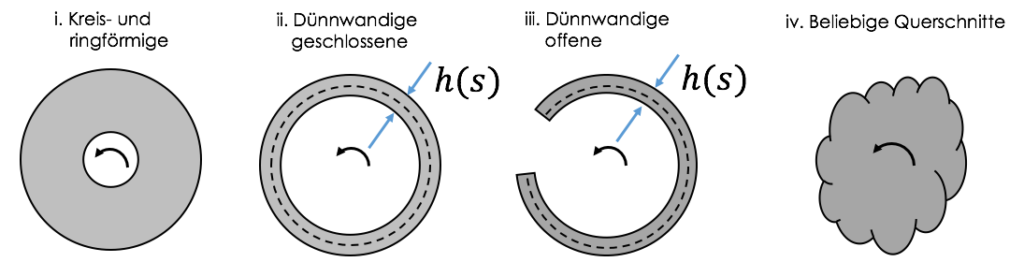
Merkmal Querschnitt:
Wichtige Formeln zu bestimmten Querschnitten:
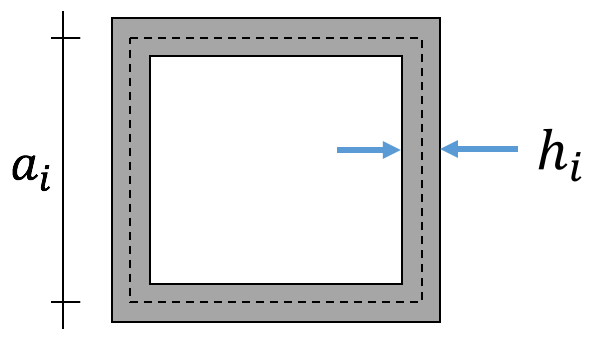
Zu ii.: $I_T=\frac{4\cdot A_m^2}{\Lambda}$ mit $\Lambda = \oint \frac{ds}{h(s)}= \sum \frac{a_i}{h_i}$
Zu iii.: $\vartheta (x)= \frac{M_T(x)}{G\cdot I_T} = \frac{\tau_{max}}{G\cdot h_{max}}, \ \tau(s)= \frac{M_T}{I_T} \cdot h(s)$, mit $I_T \stackrel{\sim}{=} \frac{\eta}{3} \cdot \sum a_i \cdot h_i^3$
Lösungsschritte (vgl. Rolf Mahnken, Lehrbuch der Technischen Mechanik – Elastostatik, Springer Verlag, 1. Auflage, 2015)
(i) für statisch bestimmte Torsionsstäbe
a. statisches System: Aufteilung in $n$ Bereiche; eintragen von Koordinatensystemen
b. Schnittgrößen
c. Querschnittswerte: $I_T, \ W_T \ \rightarrow$ Tabelle
d. Schubspannungen: In Abhängigkeit der Querschnittsform
$\bullet$ Kreis- und Kreisring: $\tau_{xs}(x,r) = \frac{M_T(x)}{I_T} \cdot r$
$\bullet$ Geschl. dünnwandig: $\tau_{xs}(x,r) = \frac{M_T(x)}{2 \cdot A_m \cdot h(s)}$
$\bullet$ Offen dünnwandig: $\tau_{max} = \frac{M_T(x)}{W_T}$
$\bullet$ Bel. Querschnitt: wird meist nicht benötigt.
e. Verdrehung: Integration von
\begin{align*}
\vartheta'(x) = \frac{M_T(x)}{G I_T}
\end{align*}
unter Berücksichtigung von $1 \cdot n$ Rand- und Übergansbedingungen. Merke: bei reiner Torsion kann die Verdrehung über
\begin{align*}
\Delta \vartheta = \frac{M_T \cdot l}{G I_T}
\end{align*}
berechnet werden.
(ii) für statisch unbestimmte Torsionsstäbe
a. statisches System
b. Querschnittswerte: $I_T, \ W_T \ \rightarrow$ Tabelle
c. Verdrehungen: Integration für jeden Einzelstab von
\begin{align*}
G I_T \vartheta'(x) = -m_T(x)
\end{align*}
unter Beachtung von $2 \cdot n$ Rand- und Übergangsbedingungen
d. Weitere Aufgabenstellungen:
z.B. Momentenverlauf über $M_T(x) = G I_T \vartheta'(x)$, Schubspannungen in Abh. des Querschnitts (s. oben)
Aufgabe Schubspannung infolge Torsion